目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
4.1运动学原理
4.2 Stewart平台运动学方程
5.完整工程文件
1.课题概述
六自由度Stewart平台的matlab模拟与仿真,模拟六自由度Stewart平台的动态变化情况以及伺服角度。
2.系统仿真结果
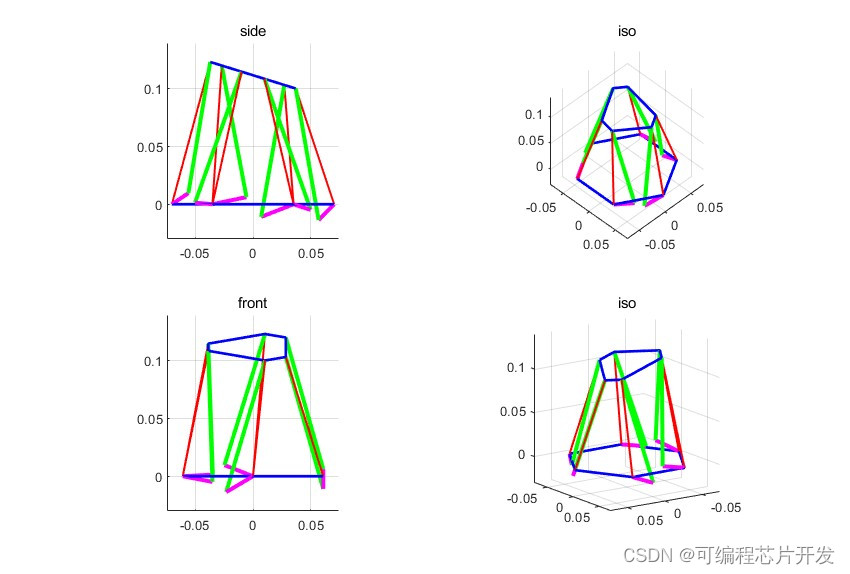
3.核心程序与模型
版本:MATLAB2022a
........................................................................
figure;
for k = 1:length(Zheave)% 遍历每个时间点,计算并绘制运动轨迹和伺服角度 % 计算基座到平台的旋转矩阵 Mrate = [cos(psi)*cos(theta), cos(psi)*sin(phi) * sin(theta) - cos(phi)*sin(psi), sin(phi)*sin(psi) + cos(phi)*cos(psi)*sin(theta);cos(theta)*sin(psi), cos(phi)*cos(psi) + sin(phi)*sin(psi)*sin(theta), cos(phi)*sin(psi)*sin(theta) - cos(psi)*sin(phi);-sin(theta), cos(theta)*sin(phi), cos(phi)*cos(theta) ];%计算有效腿长 T = [Xsurge(k) Ysway(k) Lsqrt+Zheave(k)]'; % 平台中心的坐标 q = repmat(T,1,6) + Mrate*Platm; % 将平台坐标转换到基座坐标系下 xq = q(1,:); % 转换后的x坐标 yq = q(2,:); % 转换后的y坐标 zq = q(3,:); % 转换后的z坐标 l = q - Base; % 计算腿长(向量) %计算伺服角度 L = sum(l.*l) - (Lleg^2 - Larm^2);% 计算L值(考虑伺服臂和腿的长度)M = 2*Larm*(zq - zb);% 计算M值(考虑z方向的差异) N = 2*Larm*(cosd(Theta3).*(xq - xb) + sind(Theta3).*(yq - yb)); % 计算N值(考虑x和y方向的差异以及伺服臂角度) alpha = asind(L./sqrt(M.^2 + N.^2)) - atand(N./M); % 计算伺服角度(逆正弦和逆正切函数) Sets(k,:) = alpha;% 存储计算得到的伺服角度 % 计算伺服臂坐标xa = Larm*cosd(alpha).*cosd(Theta3) + xb;ya = Larm*cosd(alpha).*sind(Theta3) + yb;za = Larm*sind(alpha) + zb;%% Plotclfsubplot(221);views;view([0,0]); title('side');subplot(222);views;view([45,45]); title('iso');subplot(223);views;view([90,0]); title('front');subplot(224);views;view([145,15]); title('iso');% select viewpause(0.00001)
endfigure
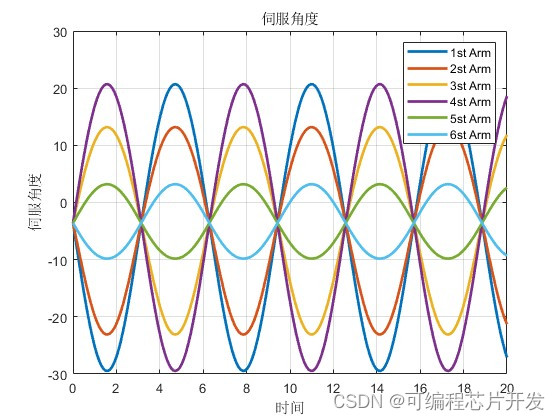
plot(Times,Sets,'LineWidth',2);
xlabel('时间');
ylabel('伺服角度');
title('伺服角度');
legend('1st Arm','2st Arm','3st Arm','4st Arm','5st Arm','6st Arm');
grid on;
354.系统原理简介
六自由度(6-DOF)Stewart平台是一种高度灵活且广泛应用的空间定位机构,它能够实现六个独立自由度的运动:三个平动自由度(X、Y、Z轴方向的直线移动)和三个转动自由度(绕X、Y、Z轴的旋转)。这种平台由一个中心平台和通过六个具有可伸缩连杆与六个固定基座相连的伺服驱动器组成,每个连杆末端装有万向节,确保任何角度下的力矩传递。
Stewart平台由上下两个平行平台(上平台为动平台,下平台为静平台)和六个可伸缩的支撑杆组成。每个支撑杆的两端分别通过球铰或虎克铰与上下平台相连。球铰可以实现三个方向的转动自由度,而虎克铰则可以实现两个方向的转动自由度。因此,通过合理选择球铰或虎克铰的连接方式,可以实现平台在空间中的六个自由度运动。
4.1运动学原理

4.2 Stewart平台运动学方程
动力学分析是求解平台在给定输入力和力矩下的运动加速度。对于Stewart平台而言,输入力和力矩为六个支撑杆的驱动力和驱动力矩,输出加速度为动平台的加速度和角加速度。

5.完整工程文件
v





)



——采样和数据驱动)






)


 浅析)