参考

理论参考：深蓝学院
实现参考：github项目

原理

引入

对于这样一个图，我们试图找到S到G的通路：

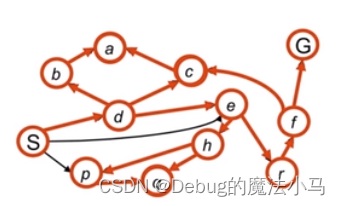
计算机程序不会像人眼一样，一下子连出一条从S到G的通路，需要一个一个节点的访问。每个节点，在建模和编程的时候都设计为一个数据结构，可以知道跟他直接连通的有哪些节点，以及这些边的代价。
我们假想自己就是程序，在访问一个节点，比如S时，看到S和p,d,e三个节点都有边。那我就可以先看看p是否和G有边，或者先看看d是否和G有边，也可以先看看e是否和G有边，这个暂时不重要。假设我们先看p是否和G有边，我们发现p和q有边，和G无边。这时候我们面临了关键选择：我是沿这条线继续深入，看看q是否和G有边哪？还是回过头开另一条线，看看d是否和G有边？这里的选择就是深度优先和广度优先的全部区别所在。

因为可以认为q是p的下一级节点，继续查看p，就是往深处探寻。就像是面对岔路口一样，我是继续选一个岔路往前走还是回到上一个岔路口，深度优先选择选一个岔路口继续深入，而且每次面对这样的选择都这么做。如果一直走到了死胡同也没到终点，再回到上一个岔路口，换一条路继续深入。

根据这个树形结构，可以更好理解，深度：

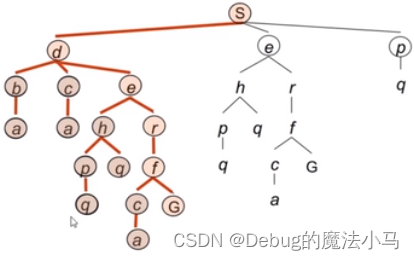
你要说，明明是图结构，为什么又变成树结构？回答是，程序面对岔路口时，并不知道地图全貌（他知道，但他不理解）。

主要的找通路问题解决了，还有两个次要问题：

1. 我们找通路是为了下次走方便的，所以要记录下来这条通路经过了哪些节点。其实我们只需要记录每一个节点的父节点，只要每个节点只有一个父节点，最后一定能回溯出唯一的一条通路
2. 我们通常不仅是要找通路，更是要找最短路径。在面临一个节点有多个父节点时，需要比较不同父节点时从起点到这个节点的累计代价和，取代价和最小的父节点为父节点。

流程解析

我们根据图搜索的一个通用模板进行流程解析：

1. 初始化节点数据结构（节点，父节点，累计代价和）。

2. 初始化开放列表openlist，把初始节点s包含其中，无父节点，累计代价和为0。

3. 初始化封闭列表closelist，没有任何东西。

4. 执行以下循环，直到所有节点被访问或通路被找到，或其他结束标准：
   3.1. 根据算法规则，从openlist中取出一个节点。
   3.2. 根据图结构，获得该节点的相邻节点（和该节点有边的节点），并排除掉在closelist中的节点
   3.3 领域查询：

   • 如果相邻节点不在openlist中，以该节点为父节点，计算累计代价值，将此相邻节点直接加入openlist。
   • 如果相邻节点在openlist中，则假设以该节点为父节点，计算此时累计代价值，并与openlist中的历史累计代价值比较：
     • 如果此时累计代价值大，则不加入openlist。
     • 反之将之前的剔除openlist，把此时的加入openlist。

   3.4. 把该节点放入closelist。
   3.5. 判断该节点是否为终止节点。

5. 终止节点的累计代价就是整条通路的累计代价；从终止节点开始查询父节点就找到了从初始节点到终止节点的整条通路。

图搜索的核心在于3.1的算法规则。对于深度优先算法，我们应该提取最近加入的节点。
举个例子就是：当我们面对岔路时，我们应该走刚看到的岔路中的一条，而不是之前看到的岔路中的一条。
这个思想直接对应于一种数据结构：堆栈。所以用堆栈管理openlist就可以实现深度优先搜索。

当然，此时还有一个小小的问题：

• 当前节点的相邻节点有好几个，他们应该以什么样的顺序压入堆栈哪？毕竟越晚被压入，越早被取出嘛，压入先后是有不同的。这点随意。比如面对一个岔路，可以顺时针编号，可以逆时针编号，这部分的优化不是深度优先算法的工作。

手推例子

道理明白了，我们结合流程，手推一遍算法的实现：
参照这个图，假设起点为S，重点为r（不用G是因为搜索过程太长了）：

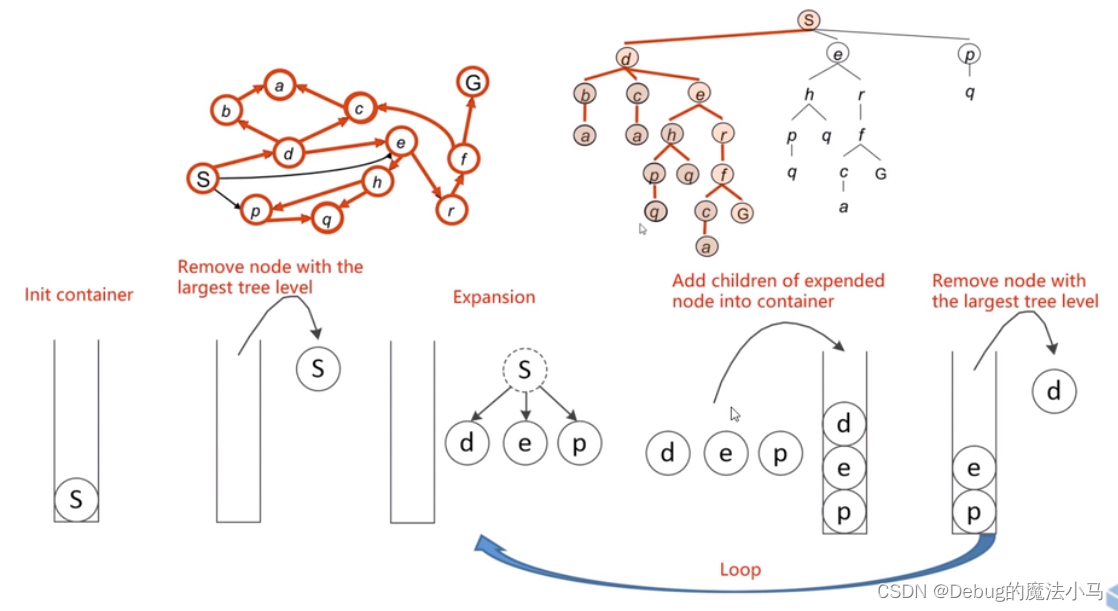
1. 初始化节点数据结构（节点，父节点，累计代价和）。
2. 初始化开放列表openlist，把初始节点s包含其中，无父节点，累计代价和为0。
3. 初始化封闭列表closelist，没有任何东西。
4. 开始循环：
   a. 弹出openlist最上层节点S；查找到邻居节点d,e,p，都不在openlist和closelist中，因此依次放进openlist,此时openlist为p,e,d；将节点S放入closelist；S没有终止节点r，继续；
   b. 弹出openlist最上层节点d，查找到邻居节点e,c,b，openlist中已经有e，但这个例子中没有定义代价，所以无法判断是否替换掉原有的e，暂时不管，依次放进openlist,此时openlist为p,e(s),e(d),c,b；将节点d放入closelist；d没有终止节点r，继续；
   c. 弹出openlist最上层节点b，查找到邻居节点a，放进openlist,此时openlist为p,e(s),e(d),c,a；将节点b放入closelist；b没有终止节点r，继续；
   d. 弹出openlist最上层节点a，查找到没有邻居节点，什么都不放入openlist，此时openlist为p,e(s),e(d),c；将节点a放入closelist；a没有终止节点r，继续；
   e. 弹出openlist最上层节点c，查找到邻居节点a，放进openlist,此时openlist为p,e(s),e(d),a；将节点c放入closelist；c没有终止节点r，继续；
   f. 弹出openlist最上层节点a，查找到没有邻居节点，此时openlist为p,e(s),e(d)；将节点a放入closelist；发现a没有终止节点r，继续；
   g. 弹出openlist最上层节点e(d)，查找到邻居节点h,r，放进openlist,此时openlist为p,e(s),h,r；将节点e(d)放入closelist；发现e(d)没有终止节点r，继续；
   h. 弹出openlist最上层节点r，查找到邻居节点f，放进openlist，此时openlist为p,e(s),h,f；把r放进closelist，r就是终止节点，循环结束
5. r父节点是e(d)，e(d)父节点是d，d父节点是s，因此通路为s-d-e-r。因为没有定义代价，所以通路累计代价值不知道。

代码实现

核心代码：

class DFS(AStar):"""DFS add the new visited node in the front of the openset"""def searching(self):"""Depth-first Searching.:return: path, visited order"""# 初始化节点数据结构（在其他文件中定义过了）# 因为是栅格地图，节点标识就用坐标标识了# 节点的父节点，由self.PARENT列表维护# 到达此节点的累计代价值，由self.g列表维护# 初始化Openlistself.PARENT[self.s_start] = self.s_start    # 维护节点的父节点；起始点父节点是自己self.g[self.s_start] = 0                    # 到达此节点的累计代价值；起始点累计代价值为0self.g[self.s_goal] = math.infheapq.heappush(self.OPEN, (0, self.s_start))# 把起始点压入openlist# 初始化Closelist（在基类中定义过了）# 和初始的Openlist一样，是个空列表# 循环直到所有节点被遍历完（Openlist空掉）while self.OPEN:# 弹出最近压入Openlist堆栈的节点_, s = heapq.heappop(self.OPEN)# 将弹出节点加入Closelist，不再访问self.CLOSED.append(s)# 如果当前节点就是终点，跳出循环if s == self.s_goal:break# 如果当前节点不是终点，进行邻域查询for s_n in self.get_neighbor(s):# 检查该邻域点是否在closelist中（他给漏掉了，我加上去：）if s_n in self.CLOSED:continue# 以当前节点为父节点的邻域节点的累计代价值 = 当前节点的累计代价值 + 从当前节点到该邻域节点代价值之和# 当前节点的累计代价值在上一次循环中被计算过，所以已知# 从当前节点到该邻域节点代价值之和，在基类中被实现，基于栅格地图哈慢炖距离，如果是障碍物则无穷new_cost = self.g[s] + self.cost(s, s_n)if s_n not in self.g:self.g[s_n] = math.inf# 如果以当前节点为父节点，此邻域节点的累计代价值更小，就把原来的剔除Openlist，把现在的加进去，并更新父节点，和累计代价值if new_cost < self.g[s_n]:  # conditions for updating Costself.g[s_n] = new_cost  # 更新累计代价值self.PARENT[s_n] = s    # 更新父节点# 检查剔除原来在openlist中的记录（他给漏掉了，我加上去：）if s_n in self.OPEN:self.OPEN.remove(s_n)# 把邻域节点压入Openlist# dfs, add new node to the front of the opensetprior = self.OPEN[0][0]-1 if len(self.OPEN)>0 else 0    # 计算新元素在列表中位置（自动的堆栈结构更好，他这个要自己维护）heapq.heappush(self.OPEN, (prior, s_n)) return self.extract_path(self.PARENT), self.CLOSED

以上代码是我在源代码，根据前一节得到的流程伪代码添加了注释和缺失步骤的版本。
可以看到，和之前说的伪代码流程除了循环中几个顺序不一样（无所谓）外，其他完全一致。

运行结果

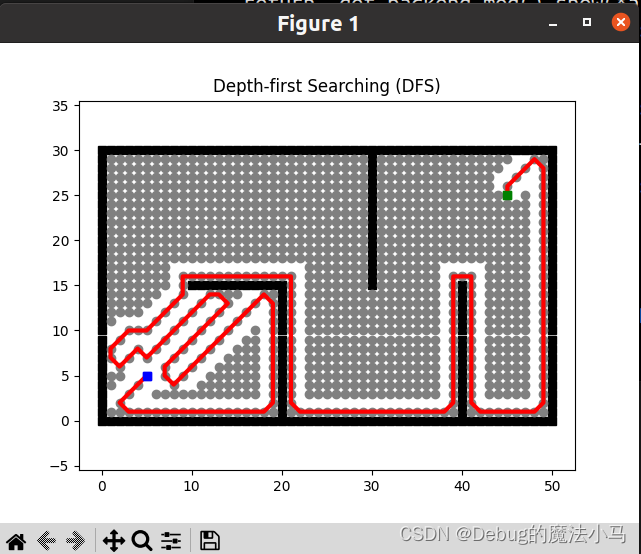
结果分析

可以看到，深度优先在面临选择时，会一条路走到黑：在有多个选择时，先一直往左下方向走；当没有选择时，溜着墙边这一条路走。

他这次表现的不好，主要是默认面临多个选择时，先探索左下角。当然你可以改成默认右上角，但这是由于我们知道了全局地图，但算法不知道，如果写死了，下次出发点在右上角，终点在左下角，还是会出现类似情况。最好的办法是让算法知道目标大概在哪个方向，这就是启发式算法做的工作了。如前所述：

当前节点的相邻节点有好几个，他们应该以什么样的顺序压入堆栈哪？毕竟越晚被压入，越早被取出嘛，压入先后是有不同的。这点随意。比如面对一个岔路，可以顺时针编号，可以逆时针编号，这部分的优化不是深度优先算法的工作。