这场没考什么算法,比较水,难度也不是很高。比赛链接
硬要说的话E有个 前缀和 加 二分,F是数学+BFS,G是个构造
A. Turtle Puzzle: Rearrange and Negate
题意:
给你一个由 n n n 个整数组成的数组 a a a 。您必须对数组执行以下两个操作(先执行第一个操作,再执行第二个操作):
- 任意重新排列数组元素或保持元素顺序不变。
- 最多选择一个连续的元素段,并将该元素段中所有元素的符号替换为相反符号。形式上,可以选择一对索引 l , r l, r l,r 这样的 1 ≤ l ≤ r ≤ n 1 \le l \le r \le n 1≤l≤r≤n 并为所有 l ≤ i ≤ r l \le i \le r l≤i≤r 指定 a i = − a i a_i = -a_i ai=−ai (符号取反)。请注意,您也可以不选择一对索引,让所有元素的符号保持不变。
在进行这两次操作后,数组元素的最大和是多少?
思路:
显然先把负的元素排到一起,然后对它们符号取反,得到的就全是正数了,这时候加起来最大
code:
#include <iostream>
#include <cstdio>
using namespace std;int T,n;
long long t;int main(){cin>>T;while(T--){cin>>n;t=0;for(int i=1,tmp;i<=n;i++){cin>>tmp;t+=abs(tmp);}cout<<t<<endl;}return 0;
}
B. Turtle Math: Fast Three Task
题意:
给你一个数组 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an 。
在一次移动中,你可以执行以下两种操作中的任何一种。您可以执行任意次数的移动:
- 从数组中选择一个元素并将其从数组中移除。这样数组的长度会减少 1 1 1 ;
- 从数组中选择一个元素并将其数值增加 1 1 1 。
如果当前数组为空,则不能再移动。
你的任务是找出使数组中的元素之和 a a a 能被 3 3 3 整除所需的最少移动次数。你可能需要走 0 0 0 步。
注意空数组(长度为 0 0 0 的数组)的元素之和等于 0 0 0 。
思路:
先把元素和算出来,如果元素和本身就模3同余0,那就就不需要动了。如果余1,那么删掉模3余1的某个元素就可以了,或者给某个元素加两次。如果余2,那么删掉模3余2的某个元素就可以了,或者给某个元素加一次。因此统计一下有无模3余1和2的元素,之后直接讨论就行了。
code:
#include <iostream>
#include <cstdio>
#include <set>
using namespace std;int T,n;int main(){cin>>T;while(T--){cin>>n;set<int> S;int tot=0;for(int i=1,t;i<=n;i++){cin>>t;tot=(t+tot)%3;S.insert(t%3);}if(tot==0){cout<<0<<endl;}else if(tot==1){if(S.count(1))cout<<1<<endl;else cout<<2<<endl;}else if(tot==2){//直接加1就完事了,还删它干嘛cout<<1<<endl;}}return 0;
}
C. Turtle Fingers: Count the Values of k
题意:
给你三个正整数 a a a 、 b b b 和 l l l ( a , b , l > 0 a,b,l\gt 0 a,b,l>0 )。
可以证明,总有一种方法可以选择非负(即 ≥ 0 \ge 0 ≥0 )的整数 k k k 、 x x x 和 y y y ,使得 l = k ⋅ a x ⋅ b y l = k \cdot a^x \cdot b^y l=k⋅ax⋅by .
你的任务是找出所有这些方法中 k k k 的不同可能值的个数。
思路:
发现 l ≤ 1 0 6 l\le 10^6 l≤106,数据范围很小,而且 x , y x,y x,y 都在指数上,根本没有很多可行的取值。所以直接暴力枚举就行了。
code:
#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
typedef long long ll;int T,a,b,l;int main(){cin>>T;while(T--){cin>>a>>b>>l;set<int> S;for(ll x=1;l%x==0;x*=a){for(ll y=1;l%y==0;y*=b){if(l%(x*y)==0)S.insert(l/x/y);}}cout<<S.size()<<endl;}return 0;
}
D. Turtle Tenacity: Continual Mods
题意:
给定数组 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an ,判断是否有可能将其元素**重排为 b 1 , b 2 , … , b n b_1, b_2, \ldots, b_n b1,b2,…,bn ,从而得到 b 1 m o d b 2 m o d … m o d b n ≠ 0 b_1 \bmod b_2 \bmod \ldots \bmod b_n \neq 0 b1modb2mod…modbn=0 。
这里的 x m o d y x \bmod y xmody 表示 x x x 除以 y y y 所得的余数。另外,模运算是从左向右计算的。即 x m o d y m o d z = ( x m o d y ) m o d z x \bmod y \bmod z = (x \bmod y) \bmod z xmodymodz=(xmody)modz 。例如, 2024 m o d 1000 m o d 8 = ( 2024 m o d 1000 ) m o d 8 = 24 m o d 8 = 0 2024 \bmod 1000 \bmod 8 = (2024 \bmod 1000) \bmod 8 = 24 \bmod 8 = 0 2024mod1000mod8=(2024mod1000)mod8=24mod8=0 。
思路:
不妨先给所有数排个序,不难发现如果最小的数只有一个,那就按顺序模就行了。
如果最小的数有多个,考虑用某个大数模它,得到比它更小的正数,然后继续像上面一样做。
但是如果得不到比最小数更小的正数,说明每个大数都是最小数 x x x 的倍数,它们互相模得到的也是 x x x 的倍数,这时无论怎么搞,都一定会被模 x x x 给干成 0 0 0,无解。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;int T,n;
int a[maxn];int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];sort(a+1,a+n+1);if(a[1]!=a[2])puts("YES");else {bool flag=false;for(int i=3;i<=n;i++){if(a[i]%a[1]){flag=true;break;}}puts((flag)?"YES":"NO");}}return 0;
}
E. Turtle vs. Rabbit Race: Optimal Trainings
题意:
艾萨克开始训练。有 n n n 条跑道可供使用, i i i 条跑道( 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n )由 a i a_i ai 个等长的部分组成。
给定一个整数 u u u ( 1 ≤ u ≤ 1 0 9 1 \le u \le 10^9 1≤u≤109 ),完成每一段都能使艾萨克的能力提高一个特定值,具体描述如下:
- 完成第 1 1 1 部分会使艾萨克的成绩提高 u u u 。
- 完成第 2 2 2 部分会使艾萨克的能力提高 u − 1 u-1 u−1 。
- 完成第 3 3 3 部分会使艾萨克的成绩提高 u − 2 u-2 u−2 。
- … \ldots …
- 完成第 k k k 部分( k ≥ 1 k \ge 1 k≥1 )会使艾萨克的成绩提高 u + 1 − k u+1-k u+1−k 。 u + 1 − k u+1-k u+1−k 的值可以是负数,这意味着完成额外的部分会降低艾萨克的成绩)。
您还得到了一个整数 l l l 。您必须选择一个整数 r r r ,使 l ≤ r ≤ n l \le r \le n l≤r≤n 和艾萨克都能完成赛道 l , l + 1 , … , r l, l + 1, \dots, r l,l+1,…,r 的个段(即总共完成 l ≤ r ≤ n l \le r \le n l≤r≤n 个段)。(即总共完成 ∑ i = l r a i = a l + a l + 1 + … + a r \sum_{i=l}^r a_i = a_l + a_{l+1} + \ldots + a_r ∑i=lrai=al+al+1+…+ar 节)。
请回答下列问题:你所能选择的最佳 r r r 是什么,能最大限度地提高艾萨克的成绩?
如果有多个 r r r 可以最大限度地提高艾萨克的成绩,请选出小的 r r r 。
为了增加难度,你需要回答 q q q 个不同值的 l l l 和 u u u 。
思路:
因为如果区间和为 u u u 或者 u + 1 u+1 u+1时,进行进行第 u u u 或 u + 1 u+1 u+1 组训练的时候收益就已经降到 1 1 1 或 0 0 0 了,之后再训练就是负数了。因此贪心的思路想就是尽量使得 [ l , r ] [l,r] [l,r] 区间和尽量等于 u u u 或者 u + 1 u+1 u+1。
因为算的是区间和,所以先用前缀和处理一下,用数组 s [ i ] s[i] s[i] 表示前 1 ∼ i 1\sim i 1∼i 位置上的和。左区间确定后,我们想要右区间的前缀和 s [ r ] s[r] s[r] 满足 s [ r ] − s [ l − 1 ] = u s[r]-s[l-1]=u s[r]−s[l−1]=u,于是 s [ r ] = s [ l − 1 ] + u s[r]=s[l-1]+u s[r]=s[l−1]+u,我们使用二分可以找到第一个 s [ r ] ≥ s [ l − 1 ] + u s[r]\ge s[l-1]+u s[r]≥s[l−1]+u 的位置,但是我们二分找到的无法保证它一定是最优的,但是我们可以保证最优的答案一定在它左边一个位置,他自己或右边一个位置,再向外找就会离 u , u + 1 u,u+1 u,u+1 越远,因此答案一定不优。我们只找一下这三个位置的收益,取最大值即可。
收益的计算式是个等差数列求和: u + ( u − 1 ) + ( u − 2 ) + ⋯ + ( u + 1 − t ) = ( u + u + 1 − t ) ∗ t 2 u+(u-1)+(u-2)+\dots+(u+1-t)=\frac{(u+u+1-t)*t}{2} u+(u−1)+(u−2)+⋯+(u+1−t)=2(u+u+1−t)∗t
实际上,它的收益函数画出来是个二次函数形状的函数,直接跑三分也是可以的。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;
const ll inf=1e18;int T,n,a[maxn];
ll s[maxn];int Q,l,u;inline ll f(ll u,ll t){return (u+u+1-t)*t/2;}int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i],s[i]=s[i-1]+a[i];cin>>Q;while(Q--){cin>>l>>u;ll ans=-inf,r;int idx=lower_bound(s+l-1,s+n+1,s[l-1]+u)-s;for(int i=max(l,idx-1);i<=min(idx+1,n);i++)if(ans<f(u,s[i]-s[l-1])){ans=f(u,s[i]-s[l-1]);r=i;}cout<<r<<" ";}cout<<endl;}return 0;
}
F. Turtle Mission: Robot and the Earthquake
题意:
世界是一个有 n n n 行和 m m m 列的网格。行的编号为 0 , 1 , … , n − 1 0, 1, \ldots, n-1 0,1,…,n−1 ,列的编号为 0 , 1 , … , m − 1 0, 1, \ldots, m-1 0,1,…,m−1 。在这个世界里,列是循环的(即每列的顶部和底部单元格是相邻的)。第 i i i 行和第 j j j 列( 0 ≤ i < n , 0 ≤ j < m 0 \le i\lt n, 0 \le j \lt m 0≤i<n,0≤j<m )上的单元格表示为 ( i , j ) (i,j) (i,j) 。
在 0 0 0 时间, ( i , j ) (i,j) (i,j) 单元格(其中 0 ≤ i < n , 0 ≤ j < m 0 \le i \lt n, 0 \le j \lt m 0≤i<n,0≤j<m 单元格)包含 ( i , j ) (i,j) (i,j) 和 0 0 0 时间。(其中 0 ≤ i < n , 0 ≤ j < m 0 \le i \lt n, 0 \le j \lt m 0≤i<n,0≤j<m 包含石或无。单元格 ( i , j ) (i,j) (i,j) 的状态可以用整数 a i , j a_{i,j} ai,j 来描述:
- 如果是 a i , j = 1 a_{i,j} = 1 ai,j=1,则 ( i , j ) (i,j) (i,j) 处有一块石头。
- 如果是 a i , j = 0 a_{i,j} = 0 ai,j=0,则 ( i , j ) (i,j) (i,j) 处什么都没有。
由于地震余震的影响,岩柱跟随构造板块运动:每个岩柱以每单位时间 1 1 1 个单元的速度循环向上移动。从形式上看,对于某个 0 ≤ i < n , 0 ≤ j < m 0 \le i \lt n, 0 \le j \lt m 0≤i<n,0≤j<m ,如果 ( i , j ) (i,j) (i,j) 中包含一块岩石,那么它将从 ( i , j ) (i, j) (i,j) 移动到 ( i − 1 , j ) (i - 1, j) (i−1,j) (如果 ( i − 1 , j ) (i - 1, j) (i−1,j) 中包含一块岩石,那么它将从 ( i , j ) (i, j) (i,j) 移动到 ( n − 1 , j ) (n - 1, j) (n−1,j) )。(或移动到 ( n − 1 , j ) (n - 1, j) (n−1,j) ,如果是 i = 0 i=0 i=0 )。
名为 RT 的机器人最初位于 ( 0 , 0 ) (0,0) (0,0) 。它必须移动到 ( n − 1 , m − 1 ) (n-1,m-1) (n−1,m−1) 处进行地震救援(移动到最右下方的单元格)。地震不会改变机器人的位置,只会改变世界中岩石的位置。
假设 RT 的当前位置为 ( x , y ) (x,y) (x,y) ( 0 ≤ x < n , 0 ≤ y < m 0 \le x \lt n, 0 \le y \lt m 0≤x<n,0≤y<m ),那么它可以在 0 ≤ x < n , 0 ≤ y < m 0 \le x \lt n, 0 \le y \lt m 0≤x<n,0≤y<m 中移动。 0 ≤ x < n , 0 ≤ y < m 0 \le x \lt n, 0 \le y \lt m 0≤x<n,0≤y<m ),它可以执行以下操作:
- 循环向上移动一格,即使用 1 1 1 单位时间从 ( x , y ) (x,y) (x,y) 移动到 ( ( x + n − 1 ) m o d n , y ) ((x+n-1) \bmod n, y) ((x+n−1)modn,y) 。
- 向下循环移动一个单元格,即以 1 1 1 为时间单位从 ( x , y ) (x,y) (x,y) 移动到 ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y) 。
- 向右移动一格,即使用 1 1 1 个时间单位从 ( x , y ) (x,y) (x,y) 到 ( x , y + 1 ) (x, y+1) (x,y+1) 。(只有在 y < m − 1 y \lt m-1 y<m−1 时,RT 才能执行此操作)。
注意,RT 不能使用操作向左移动,也不能停留在某一位置。
不幸的是,RT 在与岩石碰撞后会爆炸。因此,当 RT 位于 ( x , y ) (x,y) (x,y) 处,而 ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y) 或 ( ( x + 2 ) m o d n , y ) ((x+2) \bmod n, y) ((x+2)modn,y) 处有一块岩石时,RT 不能向下移动,否则就会被岩石击中。
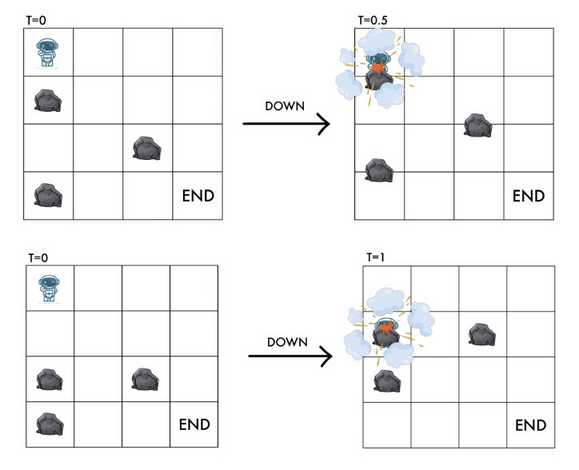
同样,如果 y + 1 < m y+1 \lt m y+1<m 和 ( ( x + 1 ) m o d n , y + 1 ) ((x+1) \bmod n, y+1) ((x+1)modn,y+1) 处有一块岩石,RT 就不能向右移动,否则就会被岩石击中。
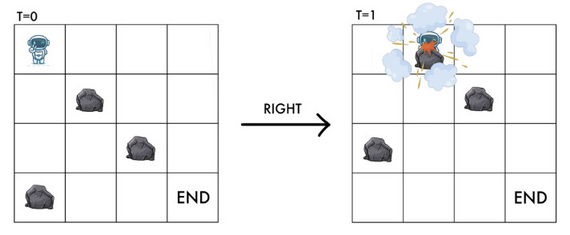
然而,值得注意的是,如果在 ( x m o d n , y + 1 ) (x \bmod n, y+1) (xmodn,y+1) 和 ( ( x + 1 ) m o d n , y ) ((x+1) \bmod n, y) ((x+1)modn,y) 处有一块岩石,RT 仍然可以安全地向右移动。
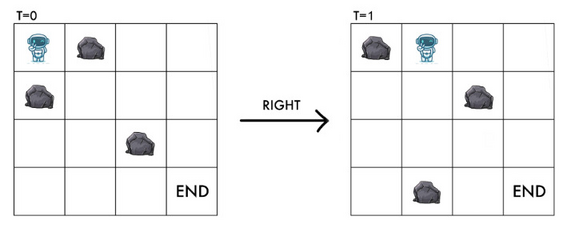
求 RT 到达 ( n − 1 , m − 1 ) (n-1,m-1) (n−1,m−1) 时不与任何岩石相撞所需的最短时间。如果无法做到,则输出 − 1 -1 −1 。
思路:
逆天长题面,读着读着就读假了,以为有个向左走的操作,然后WA一小时的test 4,恶心人。
先说好,行是从 0 ∼ n − 1 0\sim n-1 0∼n−1,列是从 0 ∼ m − 1 0\sim m-1 0∼m−1,方便取模 模拟循环。
石头可能有很多,我们不可能每次移动都算一下石头在哪里,所以我们根据相对论,不如把石头看成静止的,把移动附加到终点和机器人的移动上。发现终点相当于每次向下移动一格,机器人向下走变成了向下走两步,向右走变成了向右下走一步,向上走变成了静止不动。
显然我们在中间是不会静止不动的,因为终点所在列没有石头,所以我们不如先跑到终点列,再看要不要静止等终点。现在就变成了用两种移动方式(向下两格,或向右下一格)跑bfs。
到终点列看如何到终点最快,由于我们在终点的时候不需要管石头,所以现在再让石头动起来,现在终点就静止了,我们要么一步一步向下走到终点,要么一步一步向上走到终点,两者取小值。假设我们已经走过了 t m tm tm 时间到达第 m − 1 m-1 m−1 列,现在在第 u x ux ux 行上。那么终点现在相当于在第 p o s = ( n − 1 + t m ) % n pos=(n-1+tm)\%n pos=(n−1+tm)%n 行上, t = a b s ( p o s − u x ) t=abs(pos-ux) t=abs(pos−ux) 就是两点间距离, n − t n-t n−t 就是走另外一条路的距离,取 m i n ( t , n − t ) min(t,n-t) min(t,n−t) 即可。
code:
#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
const int maxn=1e3+5;
const int inf=1e9;int T,n,m;struct state{int x,y;state(int x,int y):x(x),y(y){};
};int fx[]={2,1},fy[]={0,1};int main(){cin>>T;while(T--){cin>>n>>m;vector<vector<int> > mp(n+1,vector<int>(m+1,0));for(int i=0;i<n;i++)for(int j=0;j<m;j++)cin>>mp[i][j];queue<state> q;vector<vector<int> > d(n+1,vector<int>(m+1,inf));int ans=inf;q.push(state(0,0));d[0][0]=0;while(!q.empty()){int ux=q.front().x,uy=q.front().y;q.pop();if(d[ux][uy]>=ans)continue;if(uy==m-1){int pos=(n-1+d[ux][uy])%n,t=abs(ux-pos);ans=min(ans,d[ux][uy]+min(t,n-t));continue;}for(int i=0,x,y;i<2;i++){x=(ux+fx[i])%n;y=uy+fy[i];if(y<0)continue;if((i==0 && mp[(ux+1)%n][uy]) || mp[x][y])continue;if(d[ux][uy]+1<d[x][y]){d[x][y]=d[ux][uy]+1;q.push(state(x,y));}}}if(ans!=inf)cout<<ans<<endl;else cout<<-1<<endl;}return 0;
}
G. Turtle Magic: Royal Turtle Shell Pattern
思路:
乌龟爱丽丝目前正在设计一个幸运饼干盒,她想把洛书的理论融入其中。
这个盒子可以看作是一个 n × m n \times m n×m 网格( n , m ≥ 5 n, m \ge 5 n,m≥5 ),其中行的编号为 1 , 2 , … , n 1, 2, \dots, n 1,2,…,n ,列的编号为 1 , 2 , … , m 1, 2, \dots, m 1,2,…,m 。每个单元格既可以是空,也可以有一个以下形状的幸运饼干:圆形或正方形。位于第 a a a 行和第 b b b 列交叉处的单元格表示为 ( a , b ) (a, b) (a,b) 。
最初,整个网格是空的。然后,爱丽丝对幸运饼干盒进行 q q q 次操作。 i i i /th操作( 1 ≤ i ≤ q 1 \le i \le q 1≤i≤q )如下:指定当前空单元格 ( r i , c i ) (r_i,c_i) (ri,ci) 和一个形状(圆形或方形),然后在单元格 ( r i , c i ) (r_i,c_i) (ri,ci) 中放入一个指定形状的幸运饼干。请注意,在进行 i i i /th操作后,单元格 ( r i , c i ) (r_i,c_i) (ri,ci) 不再为空。
在所有操作和之后的每一次 q q q 操作之前,爱丽丝想知道在所有剩余的空单元格中放置幸运饼干的方法有多少种,从而满足以下条件:
没有三个连续的单元格(水平方向、垂直方向和对角线方向)包含相同形状的饼干。形式上
- 不存在满足 1 ≤ i ≤ n , 1 ≤ j ≤ m − 2 1 \le i \le n, 1 \le j \le m-2 1≤i≤n,1≤j≤m−2 条件的 ( i , j ) (i,j) (i,j) ,即 ( i , j ) , ( i , j + 1 ) , ( i , j + 2 ) (i,j), (i,j+1), (i,j+2) (i,j),(i,j+1),(i,j+2) 单元格中有相同形状的饼干。
- 不存在满足 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m 1 \le i \le n-2, 1 \le j \le m 1≤i≤n−2,1≤j≤m 条件的 ( i , j ) (i,j) (i,j) ,即 ( i , j ) , ( i + 1 , j ) , ( i + 2 , j ) (i,j), (i+1,j), (i+2,j) (i,j),(i+1,j),(i+2,j) 单元格中存在形状相同的饼干。
- 不存在满足 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m − 2 1 \le i \le n-2, 1 \le j \le m-2 1≤i≤n−2,1≤j≤m−2 条件的 ( i , j ) (i,j) (i,j) ,即 ( i , j ) , ( i + 1 , j + 1 ) , ( i + 2 , j + 2 ) (i,j), (i+1,j+1), (i+2,j+2) (i,j),(i+1,j+1),(i+2,j+2) 单元格中有形状相同的曲奇饼干。
- 不存在满足 1 ≤ i ≤ n − 2 , 1 ≤ j ≤ m − 2 1 \le i \le n-2, 1 \le j \le m-2 1≤i≤n−2,1≤j≤m−2 条件的 ( i , j ) (i,j) (i,j) ,即 ( i , j + 2 ) , ( i + 1 , j + 1 ) , ( i + 2 , j ) (i,j+2), (i+1,j+1), (i+2,j) (i,j+2),(i+1,j+1),(i+2,j) 单元格中有形状相同的曲奇饼干。
您应该输出所有答案的模数 998244353 998244353 998244353 。另外请注意,在经过一些操作后,有可能已经放置的糖果已经不满足条件,在这种情况下,您应该输出 0 0 0 。
思路:
建议看这个讲解。就是个构造,发现只有八种情况能构造成功,然后一个一个暴力对一下看看能不能行。放G题算是有点德不配位了。
code:
#include <iostream>
#include <cstdio>
#include <set>
#include <cstring>
using namespace std;int T,n,m,q;
string str[2]={"circle","square"};int main(){cin>>T;while(T--){cin>>n>>m>>q;set<int> S;for(int i=1;i<=8;i++)S.insert(i);cout<<8<<endl;string t;for(int i=1,x,y;i<=q;i++){cin>>x>>y>>t;x--;y--;int ans=0;if(S.count(1)){if(str[(x+y%4/2)&1]!=t)S.erase(1);}if(S.count(2)){if(str[(x+(y+3)%4/2)&1]!=t)S.erase(2);}if(S.count(3)){if(str[(x+(y+2)%4/2)&1]!=t)S.erase(3);}if(S.count(4)){if(str[(x+(y+1)%4/2)&1]!=t)S.erase(4);}if(S.count(5)){if(str[(x%4/2+y)&1]!=t)S.erase(5);}if(S.count(6)){if(str[((x+3)%4/2+y)&1]!=t)S.erase(6);}if(S.count(7)){if(str[((x+2)%4/2+y)&1]!=t)S.erase(7);}if(S.count(8)){if(str[((x+1)%4/2+y)&1]!=t)S.erase(8);}cout<<S.size()<<endl;}}return 0;
}
更快)


)













)

