目录

力扣733.图像渲染

力扣200.岛屿数量

力扣695岛屿最大面积

力扣130.被围绕的区域（微难）

---

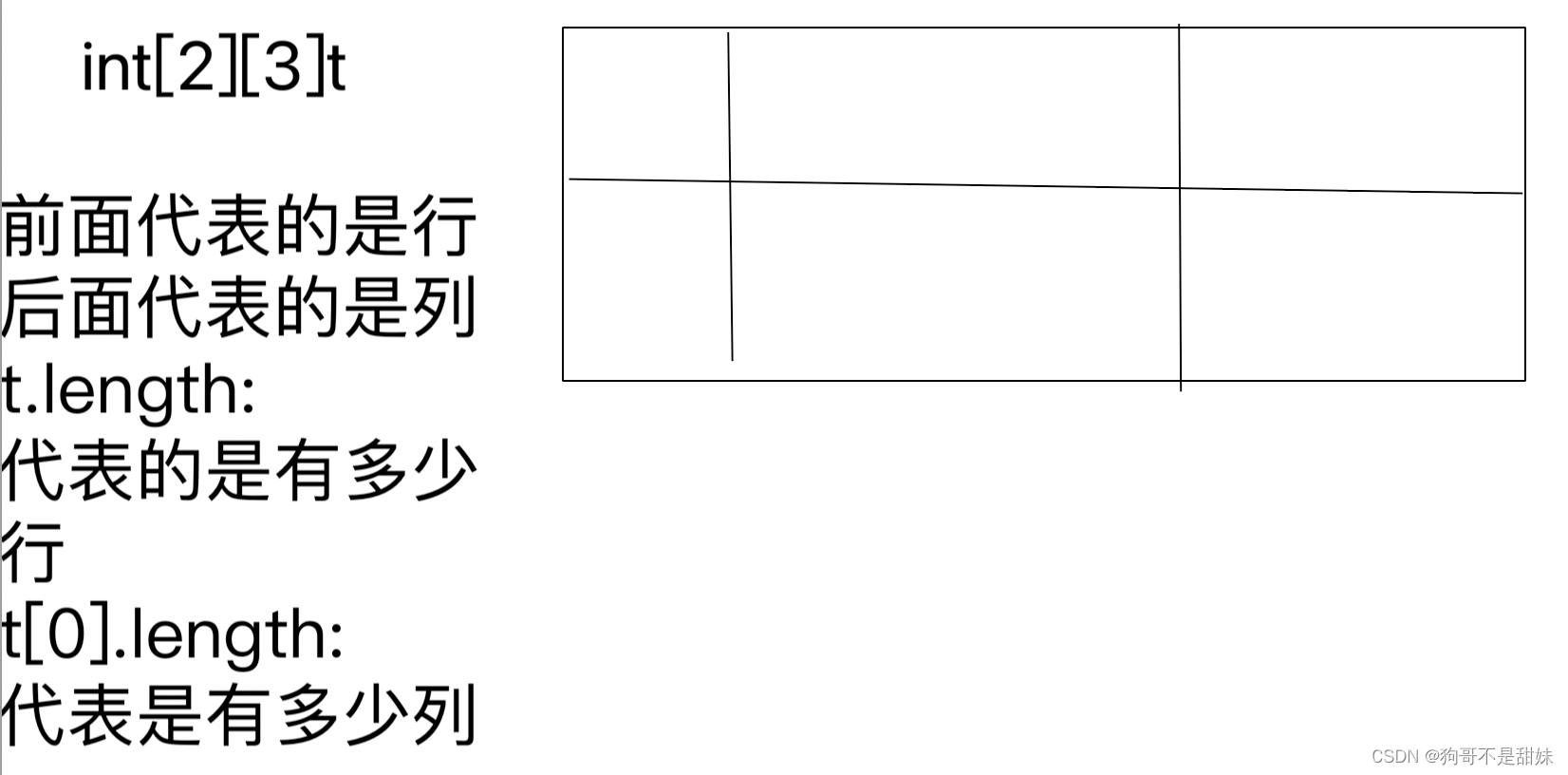
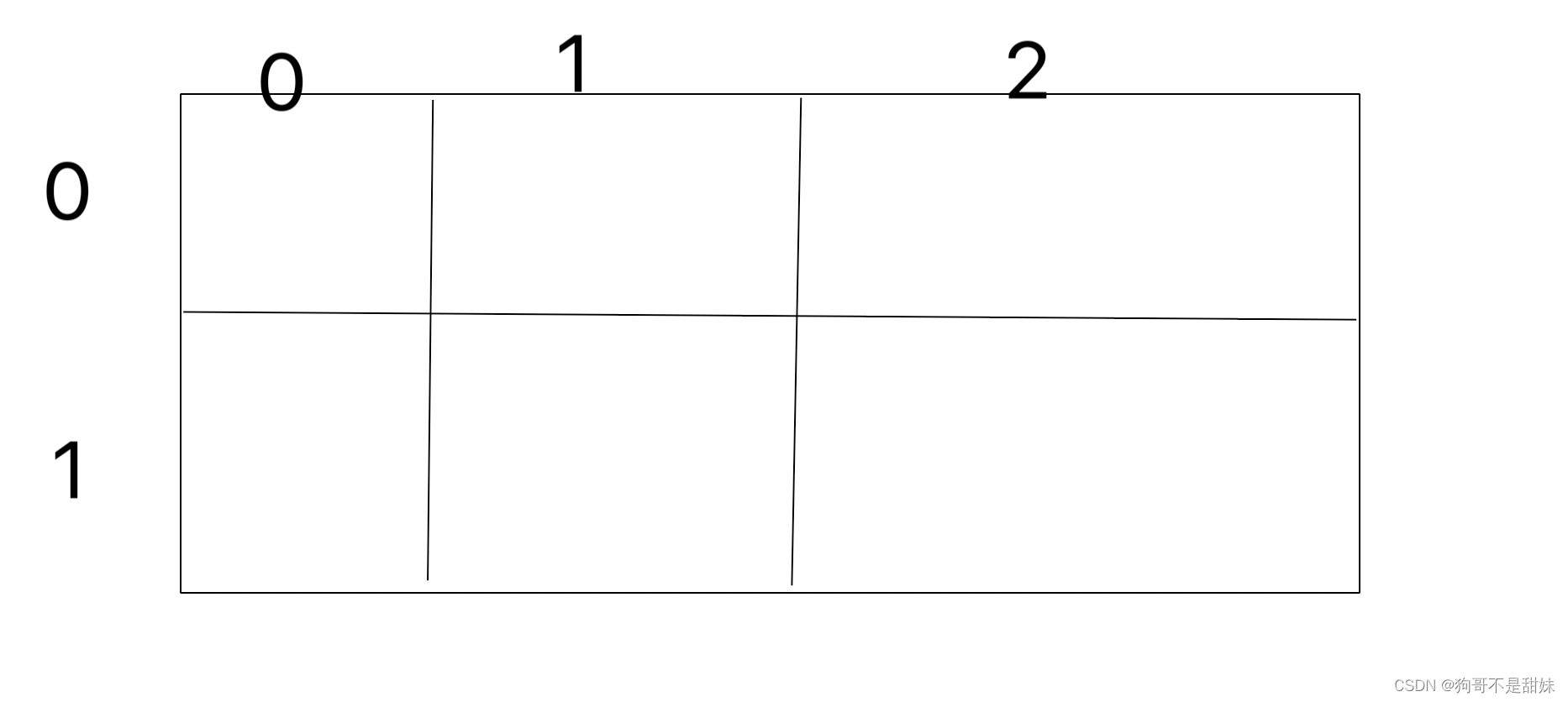
 int[2][3]

力扣733.图像渲染

FloodFill算法

洪水灌溉

广度优先遍历的本质就是暴力遍历  把所有的结果都走一遍（具体说怎么走的方向没有谈及，说是二叉树遍历，但是实际上也就是一层全部走完，并没有什么特定的规律说是往哪里走完)

class Solution {int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};public int[][] floodFill(int[][] image, int sr, int sc, int color) {int prev=image[sr][sc];if(prev==color) return image;//m是横着的下标和，n是竖着的下标和int m=image.length,n=image[0].length;Queue<int[]>q=new LinkedList<>();//把初始两个下标放到了数组里面，然后队列add的是这个数组q.add(new int[]{sr,sc});while(!q.isEmpty()){//取出队列的开头int []t=q.poll;//a,b表示的是取出来的下标int a=t[0],b=t[1];image[a][b]=color;//为什么是小于4因为对应的是4个方向for(int i=0;i<4;i++){int x=a+dx[i],y=b+dy[i];//看他越不越界，并且看他是否和目标元素相同,而且因为我们是边遍历，边去修改，所以最开始的值是发生变化了，所以不回再次进入循环if(x>=0&&x<m&&y<n&&image[x][y]==prev){//把符合要求数值下标加入队列里面，然后q.add(new int[]{x,y});}}}return image;}
}

力扣200.岛屿数量

1.直接修改原数组

2.vis[m][n]实施标记，在原先的数组情况下，给予一层标记，遍历过的使用true;

这里比较难的地方是他的代码编写，思想其实挺好理解，存下标，用一个队列存储，然后看是不是你要的（唯一比较难的根据题意，上一道题是找相同的数，这个题意很清晰，但是这道题是要找所谓的“岛屿”，这也需要你理解这个所谓的岛屿什么的究竟是什么意思，这道题，他的岛屿的含义就是把周围的一圈是陆地的都标记了，假如说周围是水，那么不耽误，假如周围不是全是水，那么把他上下左右标记一圈，到达下一个然后看扫描你的上下左右，看你的上下左右有没有也是岛屿的，假如遇到标记的就跳过。

生活思维:岛屿是被水包围的，总想是围棋一样，我们未培养起来编程思维，就感觉不知道从何下手

但是编程思维，就是先把一圈走了，看看上下左右的分布，是陆地的标记，他能把从第一个开始到不是这块的，都统计为一个，然后是水的就不标记，直接跳过，直到再找到一块岛屿，在遍历他的周围，周围没有的话，就再加一以此反复。

class Solution {int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};boolean[][] vis=new boolean[301][301];int m,n;public int numIslands(char[][] grid) {m=grid.length;n=grid[0].length;int ret=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if (grid[i][j]=='1'&&vis[i][j]==false){ret++;bfs(grid,i,j);}}}return ret;}public void bfs(char[][]grid,int i,int j){//在q里和那个图像渲染一样，在q里加入初始位置的下标Queue<int[]>q=new LinkedList<>();q.add(new int[]{i,j});vis[i][j]=true;while(!q.isEmpty()){int[]t=q.poll();int a=t[0],b=t[1];for(int k=0;k<4;k++){int x=a+dx[k],y=b+dy[k];if(x>=0&& x<m&& y>=0&& y<n&&grid[x][y]=='1' && vis[x][y]==false){q.add(new int[]{x,y});vis[x][y]=true;  }} }}
}

力扣695岛屿最大面积

class Solution {int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};int sum=0;int m,n;boolean[][]vis=new boolean[51][51];public int maxAreaOfIsland(int[][] grid) {m=grid.length;n=grid[0].length;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1&&vis[i][j]==false)sum=Math.max(sum,bfs(grid,i,j));}}
return sum;}public int bfs(int[][]grid,int i,int j){int count=0;Queue<int[]>q=new LinkedList<>();q.add(new int[]{i,j});vis[i][j]=true;count++;while(!q.isEmpty()){int[]t=q.poll();int a=t[0];     int b=t[1];for(int k=0;k<4;k++){int x=a+dx[k];int y=b+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&vis[x][y]==false&&grid[x][y]==1){        q.add(new int[]{x,y});count++;vis[x][y]=true;}}}return count;}}

力扣130.被围绕的区域（微难）

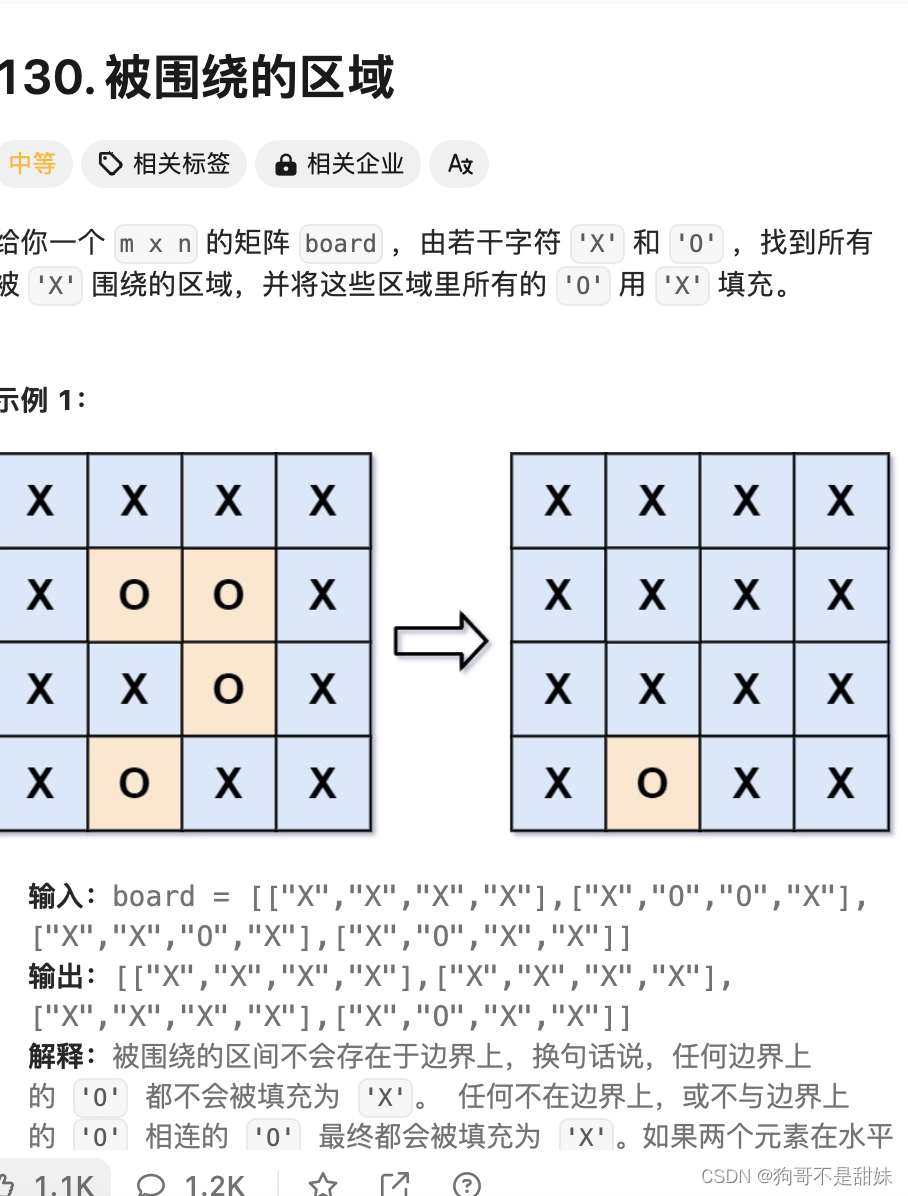
恶补二维数组知识

 

为神马说他微难呢？是因为当我们想用套模版莽夫做这个题，会发现一个问题，就是他怎么判断是否被包围，我们之前的都是边判断边修改，这个需要你看一圈之后，才判断是否需要修改。

解法:正难则反：先去把周围都给处理改成一个点，不影响判断的，只要把四边相邻的处理（这些事不被包围的）然后再去扫描矩阵，然后再去恢复成O

注意：小细节，这道题不需要统计xx数量，所以不需要我们搞一个boolean去标记

此外，这个题的正难则反，是bfs也去用来扫描矩阵，而中间的都是被包围的，所以不需要做处理，只需要都遍历的时候，把中间的一圈改成x,因为未被包围的我们都改成.了，所以不会影响我们操作，最后把.换回X即可

class Solution {int[]dx={0,0,1,-1};int[]dy={1,-1,0,0};int m,n;public void solve(char[][] board) {m=board.length;n=board[0].length;for(int i=0;i<m;i++){if(board[i][0]=='O')bfs(board,i,0);if(board[i][n-1]=='O')bfs(board,i,n-1);}for(int j=0;j<n;j++){if(board[0][j]=='O')bfs(board,0,j);if(board[m-1][j]=='O')bfs(board,m-1,j);}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(board[i][j]=='O')board[i][j]='X';else if(board[i][j]=='.')board[i][j]='O';}}}public void bfs(char[][]board,int i,int j){Queue<int[]>q=new LinkedList<>();q.add(new int[]{i,j});board[i][j]='.';while(!q.isEmpty()){int[]t=q.poll();int a=t[0];int b=t[1];for(int k=0;k<4;k++){int x=a+dx[k];int y=b+dy[k];if(x>0&&x<m-1&&y>0&&y<n-1&&board[x][y]=='O'){q.add(new int[]{x,y});board[x][y]='.';  }}   }}
}