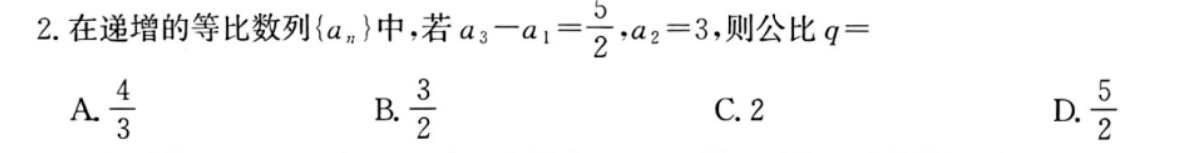解题：原式＝
2. 在递增的等比数列 ( a n ) (a_n) (an)中，若 ( a 3 − a 1 = 5 2 ) (a_3 - a_1 = \frac{5}{2}) (a3−a1=25), ( a 2 = 3 ) (a_2 = 3) (a2=3), 则公比 (q) =
A. ( 4 3 ) ( \frac{4}{3} ) (34)
B. ( 3 2 ) ( \frac{3}{2} ) (23)
C. 2
D. ( 5 2 ) ( \frac{5}{2} ) (25)
为找到公比q， [ a n = a 1 ⋅ q ( n − 1 ) ] [ a_n = a_1 \cdot q^{(n-1)} ] [an=a1⋅q(n−1)]
[ a 3 = a 1 ⋅ q ( 3 − 1 ) = a 1 ⋅ q 2 ] [ a_3 = a_1 \cdot q^{(3-1)} = a_1 \cdot q^2 ] [a3=a1⋅q(3−1)=a1⋅q2];
[ a 2 = a 1 ⋅ q ( 2 − 1 ) = a 1 ⋅ q ] [ a_2 = a_1 \cdot q^{(2-1)} = a_1 \cdot q ] [a2=a1⋅q(2−1)=a1⋅q]
所以有：
[ a 3 − a 1 = 5 2 ] [ a 1 ⋅ q 2 − a 1 = 5 2 ] [ a 1 ⋅ ( q 2 − 1 ) = 5 2 ] [ q 2 − 1 = 5 2 a 1 ] [ q 2 = 5 2 a 1 + 1 ] [ q 2 = 5 + 2 a 1 2 a 1 ] [ a_3 - a_1 = \frac{5}{2} ] [ a_1 \cdot q^2 - a_1 = \frac{5}{2} ] [ a_1 \cdot (q^2 - 1) = \frac{5}{2} ] [ q^2 - 1 = \frac{5}{2a_1} ] [ q^2 = \frac{5}{2a_1} + 1 ] [ q^2 = \frac{5 + 2a_1}{2a_1} ] [a3−a1=25][a1⋅q2−a1=25][a1⋅(q2−1)=25][q2−1=2a15][q2=2a15+1][q2=2a15+2a1]
[ q = a 2 a 1 = 3 a 1 ] [ q = \frac{a_2}{a_1} = \frac{3}{a_1} ] [q=a1a2=a13]
[ ( 3 a 1 ) 2 = 5 + 2 a 1 2 a 1 ] [ \left(\frac{3}{a_1}\right)^2 = \frac{5 + 2a_1}{2a_1} ] [(a13)2=2a15+2a1]
[ 9 = 5 + 2 a 1 2 a 1 ] [ 18 a 1 = 5 + 2 a 1 ] [ 16 a 1 = 5 ] [ a 1 = 5 16 ] [ 9 = \frac{5 + 2a_1}{2a_1} ] [ 18a_1 = 5 + 2a_1 ] [ 16a_1 = 5 ] [ a_1 = \frac{5}{16} ] [9=2a15+2a1][18a1=5+2a1][16a1=5][a1=165]
[ q = 3 a 1 = 3 5 16 = 48 5 = 24 5 = 4 1 = 4 ] [ q = \frac{3}{a_1} = \frac{3}{\frac{5}{16}} = \frac{48}{5} = \frac{24}{5} = \frac{4}{1} = 4 ] [q=a13=1653=548=524=14=4]
