【数据结构初阶 7】二叉树：链式二叉树的基本操作实现

文章目录

🌈 Ⅰ 定义二叉树结点
🌈 Ⅱ 创建二叉树结点
🌈 Ⅲ 遍历二叉树
- 1. 先序遍历
- 2. 中序遍历
- 3. 后序遍历
- 4. 层序遍历
🌈 Ⅳ 销毁二叉树

🌈 Ⅰ 定义二叉树结点

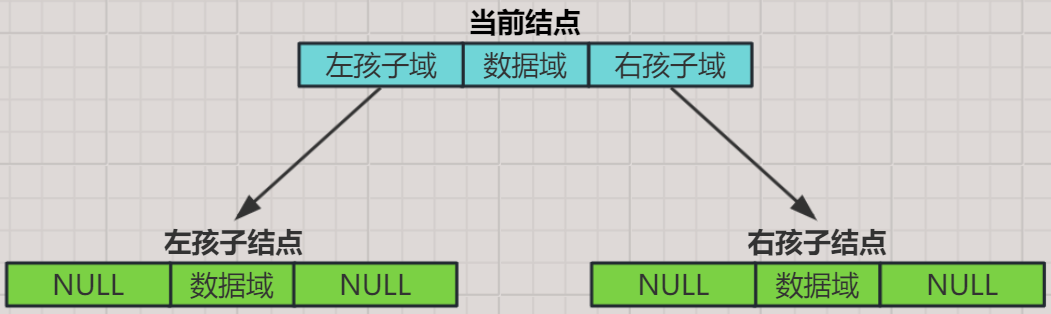
1. 每个结点都由三部分组成

数据域：存储本结点的数据。
左孩子域：存储该结点左孩子的地址，即指向该结点左子树的根结点。
右孩子域：存储该结点右孩子的地址，即指向该结点右子树的根结点。

2. 定义二叉树结点

typedef int BTDataType;typedef struct TreeNode			// 树结点
{BTDataType data;			// 数据域struct TreeNode* lchild;	// 左孩子域struct TreeNode* rchild;	// 右孩子域
}TreeNode;

🌈 Ⅱ 创建二叉树结点

malloc 一个新结点，然后将数据放进该结点数据域，新结点左右孩子都为空。

TreeNode* BuyTreeNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node);node->data = x;						node->lchild = node->rchild = NULL;	// 新结点的左右孩子域都为空return node;
}

🌈 Ⅲ 遍历二叉树

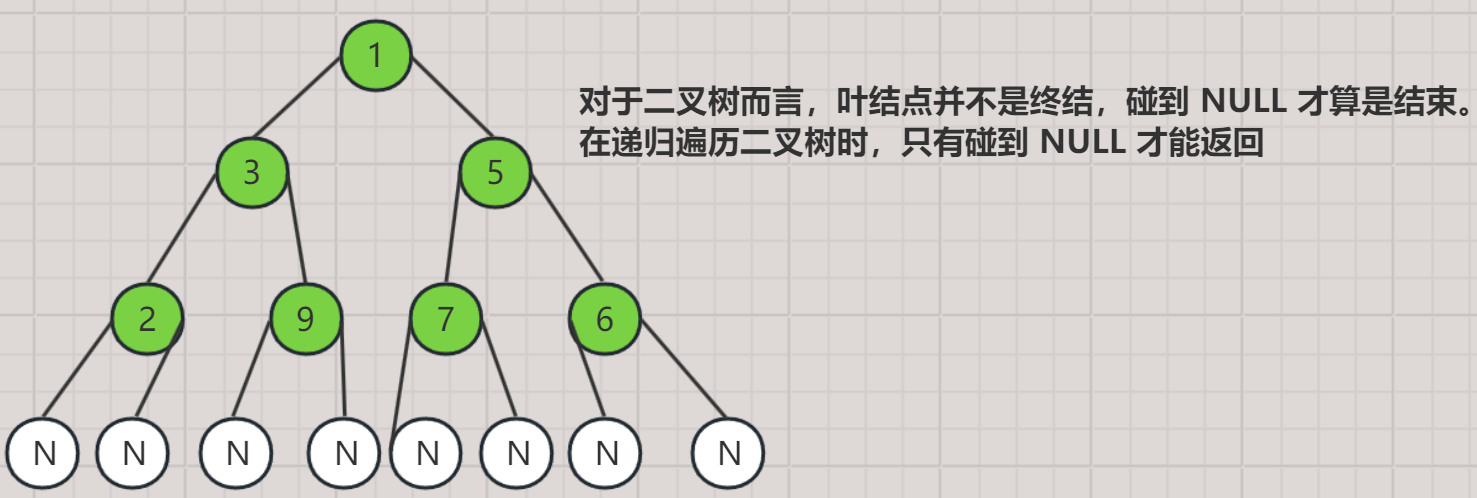
递归遍历的结束条件

当递归到某个结点为 NULL 时返回，计算机不知道哪个结点为叶子结点，只有当递归到某个结点的左右孩子域都为 NULL 时才能确定该结点为叶结点。

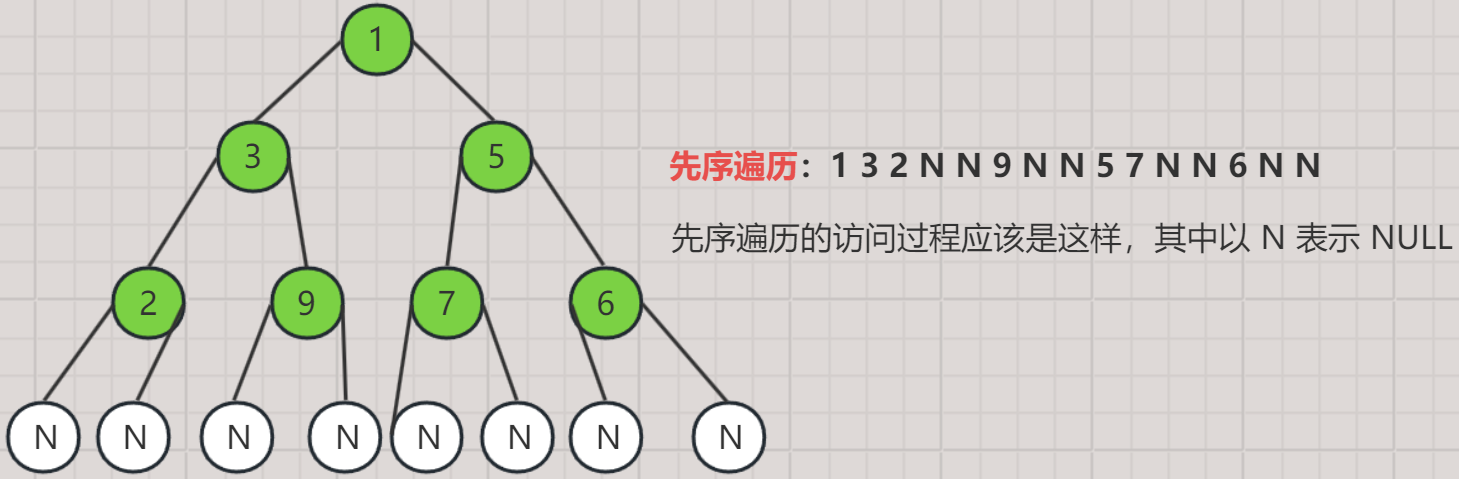
1. 先序遍历

对于一棵二叉树，其中任意一棵子树都按照根结点、左子树、右子树的顺序访问。
访问完当前结点后就去访问其左子树，左子树访问完后就去访问该结点右子树。
对于该结点左右子树的访问方式和第二步一致。

// 先序遍历
void TreePrevOrder(TreeNode* root)
{if (NULL == root)					// 结点为空时返回{return;}printf("%d ", root->data);		// 先访问当前结点TreePrevOrder(root->lchild);	// 当前结点访问完了就去访问左子树TreePrevOrder(root->rchild);	// 左子树也访问完了最后去访问右子树
}

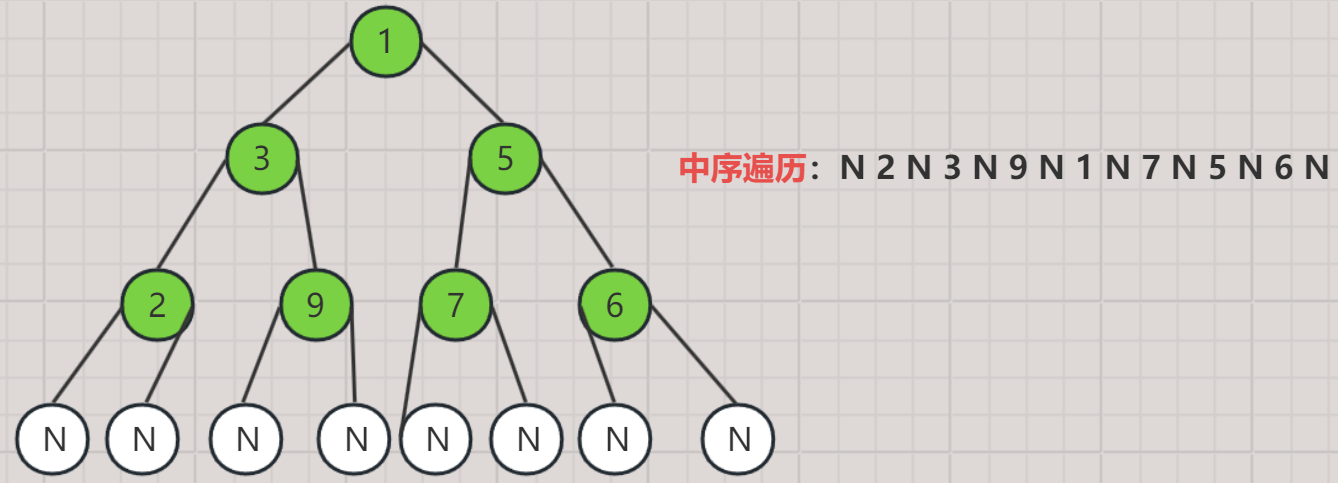
2. 中序遍历

按照左子树 → 当前结点 → 右子树的顺序访问树中的每棵子树。
对于树中的任意结点，在访问完该结点的左子树之前都不能访问该结点。

// 中序遍历
void TreeInOrder(TreeNode* root)
{if (NULL == root){return;}TreePrevOrder(root->lchild);	// 优先访问当前结点的左子树printf("%d ", root->data);		// 访问完当前结点的左子树后才能访问该结点TreePrevOrder(root->rchild);	// 最后才能去访问右子树
}

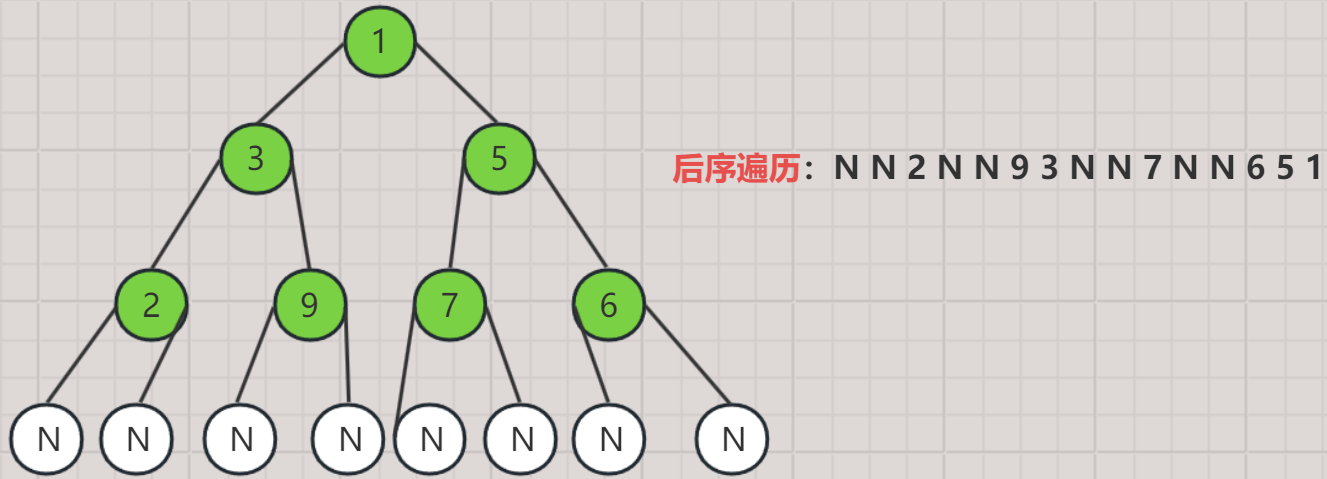
3. 后序遍历

按照左子树 → 右子树 → 当前结点的顺序访问树中的每棵子树。
对于树中的任意结点，在访问完该结点的左子树和右子树之前都不能访问该结点。

// 后续遍历
void TreePostOrder(TreeNode* root)
{if (NULL == root){return;}TreePrevOrder(root->lchild);	// 优先访问当前结点的左子树TreePrevOrder(root->rchild);	// 然后访问当前结点的右子树printf("%d ", root->data);		// 最后才能访问当前结点
}

4. 层序遍历

实现思路

借助队列进行层次遍历。
将当前结点放入队列，然后出队列。
出队列时，该结点还要顺带将其非空的左右孩子结点也入队列。
等到队列为空时，这样出队列的结点顺序就是二叉树的层序遍历结果。

举个例子

实现代码

void TreeLevelOrder(TreeNode* root)
{Queue q;								// 创建队列QueueInit(&q);							// 队列初始化if (root != NULL)						// 将非空结点入队列{QueuePush(&q, root);}int LevelSize = 1;						// 用来记录每层结点的个数while (!QueueEmpty(&q))					// 队列非空时二叉树没有遍历完{while (LevelSize--)					// 控制一层一层输出结点{TreeNode* front = QueueFront(&q);QueuePop(&q);					// 队头结点出队列printf("%d ", front->data);		// 打印队头结点的值if (front->left != NULL)		// 出队时将其非空左孩子结点入队{QueuePush(&q, front->left);}if (front->right != NULL)		// 出队时将其非空右孩子结点入队{QueuePush(&q, front->right);}}printf("\n");						// 输出完一层的结点就换行LevelSize = QueueSize(&q);			// 队列内元素个数就是下一层结点数}QueueDestroy(&q);						// 销毁队列
}

🌈 Ⅳ 销毁二叉树

采用后序的方式删除二叉树，先删完左右子树再删根结点。
对于树中的每棵子树都采用上述方法。

void TreeDestory(TreeNode* root)
{if (NULL == root){return;}TreeDestory(root->lchild);	// 先删左子树TreeDestory(root->rchild);	// 再删右子树free(root);					// 最后删根结点
}