【二分查找算法】的时间复杂度为O(log n),其中n为数组的长度。因为每次查找都将查找范围缩小一半,所以算法的时间复杂度是对数级别的。
目录
前言
二分查找算法是什么?
算法实现
方式一:(左闭右闭)
文字描述
流程图展示
案例分析
代码示例
方式二:(左闭右开)
流程图差异
代码示例:
注意事项:
代码优化
总结
前言
在生活中,我们经常会接触到查找。不同的查找方式效率也会有所不同,今天就来了解一下【二分查找算法】。首先,进入到如下场景中:
思考: 假设,有一个存在n个元素的升序排序数组(如下图),需要查找某个目标值在数组中的索引值。一般会如何去实现?

按照我们正常的思路,可能首先想到的是遍历该数组,依次将每一个元素和目标值比较,直到找到目标值,返回索引,否则返回-1。代码示例如下:
package com.zhy.algorithm;public class LineSearch {/*** 返回目标值在升序数组中的索引,找不到返回-1。* 线性实现方式* @return*/public static int lineSearchM(int[] a,int target){for(int i = 0; i < a.length; i++){if (target == a[i]){return i;}}return -1;}
}
上面的实现方法,从代码行数来看,可谓是简洁,也更易于理解。但这样写会出现什么样的弊端呢?
通过几个场景来分析一下:
- 场景1:查找目标值5在数组中的索引值:使用【线性查找】需要5次才能找到;而如果采用【二分查找法】,只用1次就能找到。
- 场景2:查找目标值7在数组中的索引值:使用【线性查找】需要7次才能找到;而如果采用【二分查找法】,只用2次就能找到。
- 场景3:查找目标值15在数组中的索引值:使用【线性查找】需要9次才能结束;而如果采用【二分查找法】,只用3次就能结束。
这么一对比,随着数据量不断增大的情况,使用【二分查找法】在时间效率上能得到很大的提升。那么我们就来看看,二分查找法究竟是怎样的一种算法?
二分查找算法是什么?
二分查找算法(Binary Search Algorithm)也叫折半查找,是一种在有序数组中查找目标值的常用算法。它的基本思想是每次将待查找的区间缩小一半,直到找到目标值或者确定目标值不存在。是一种效率较高的查找算法。
算法实现
方式一:(左闭右闭)
左闭右闭指的是,在查找过程中,左边界和右边界都包含在查找范围内。也就是说,当找到当前中间元素与目标元素相等时,直接返回中间元素的位置。左闭右闭的写法是:while(left <= right)。
文字描述
首先,了解一下二分查找算法具体的步骤如下:
- 初始化区间的起始位置left = 0,终止位置right = 数组的长度减1。
- 计算区间的中间位置(middle):middle = (left + right) / 2。
- 比较中间位置的值与目标值的大小关系:
- 如果中间值等于目标值,则找到目标值,返回中间位置。
- 如果中间值大于目标值,则更新right = middle - 1,继续下一轮查找。
- 如果中间值小于目标值,则更新left = middle + 1,继续下一轮查找。
- 重复步骤2和步骤3,直到left > right,表示找不到目标值,返回-1。
流程图展示
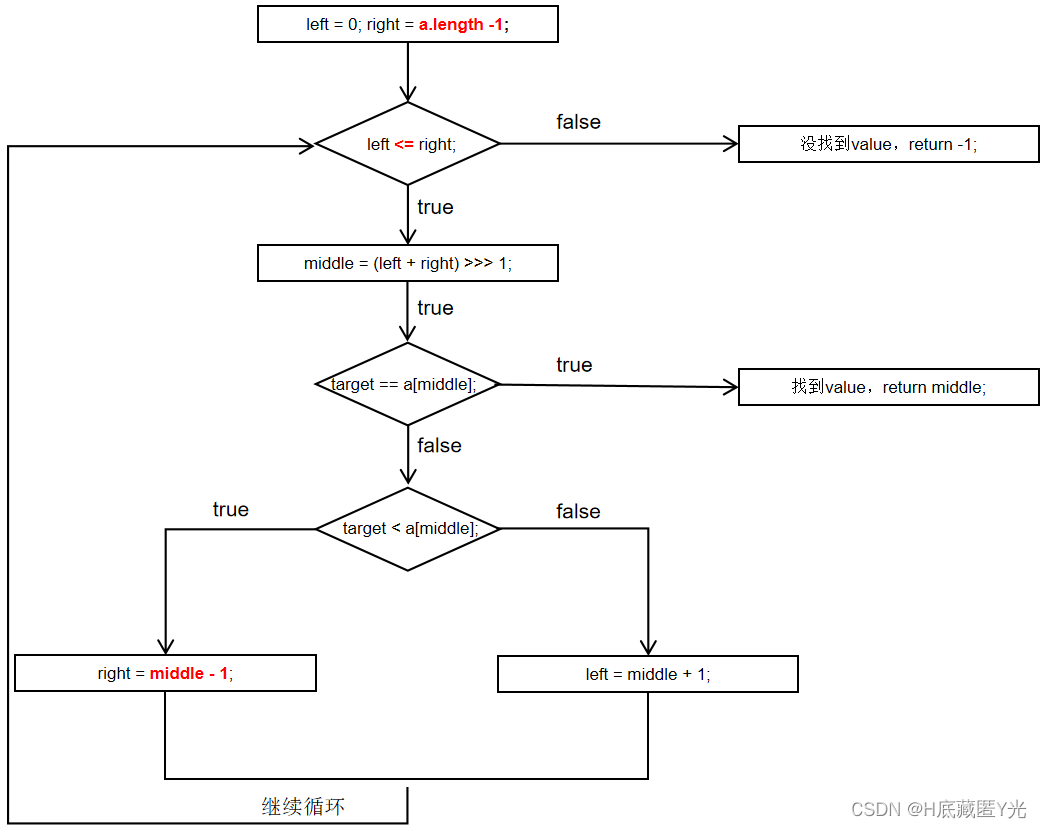
案例分析
下面,通过两个具体的案例,逐步了解一下算法的执行步骤:
案例一:从下面列表a中查找目标值8的索引。(找到的场景)

案例二: 从下面列表a中查找目标值20的索引。(找不到的场景)
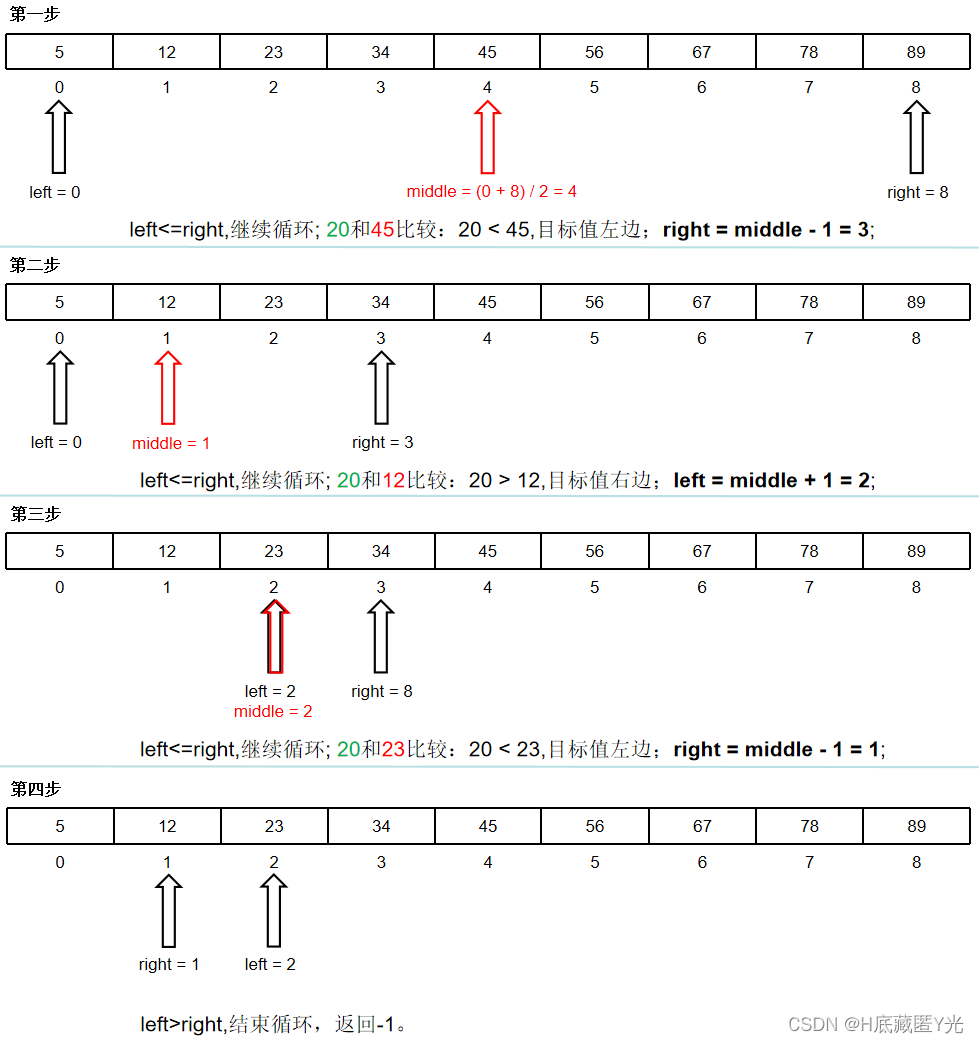
代码示例
了解了二分查找算法的核心思想,那代码实现起来也不算难,代码示例如下:
package com.zhy.algorithm;public class BinarySearch {/*** 二分查找法实现方式一:(左闭右闭)*/public static int binarySearchOne(int[] a,int target){//1.记录数组的两端索引int left = 0;int right = a.length - 1;//2.循环两端索引在中间的数据,判定条件,当left <= right时,证明还有元素while (left <= right){//求left和right的一个中间索引int middle = (left + right) >>> 1;//用中间索引的值和目标值进行比较if (target == a[middle]){//1.目标值 == 中间值,可以确定,找到了,返回middlereturn middle;}else if(a[middle] < target){//2.目标值大于中间值的情况下,可以确定,目标值在右边,left索引往右移left = middle + 1;}else {//3.目标值小于中间值的情况下,可以确定,目标值在左边,right索引往左移right = middle - 1;}}//3.如果循环结束,没有找到,返回-1return -1;}public static void main(String[] args) {int[] a = {1,2,3,4,5,6,7,8,9};int target = 51;System.out.println("找到的场景:");for (int i = 0; i < a.length; i++){System.out.println("元素 " + a[i] + " 在数组中的位置为:" + binarySearchOne(a,a[i]));}System.out.println("\n没找到的场景:");System.out.println(target + " 在数组中的位置为:" + binarySearchOne(a,target));}
}

方式二:(左闭右开)
左闭右开指的是,在查找过程中,左边界包含在查找范围内,但右边界不包含在查找范围内。也就是说,当找到当前中间元素与目标元素相等时,不返回中间元素的位置,而是将右边界设为中间元素的位置,继续向左查找。左闭右开的写法是:while(left < right)。
可以用于对有序数组进行插入、删除等操作,因为当插入或删除一个元素时,不会改变数组的有序性,而左闭右开的写法可以保证查找时不会遗漏目标元素。但在普通的二分查找中,使用左闭右闭的写法就足够了。
这两种实现方式的差异并不大,它们之间也不存在什么性能,下面我们一起看看实现差异:
流程图差异

代码示例:
package com.zhy.algorithm;public class BinarySearch {/*** 二分查找法实现方式二:(左闭右开)*/public static int binarySearchOne(int[] a,int target){//1.记录数组的两端索引int left = 0;int right = a.length;//2.循环两端索引在中间的数据,判定条件,当left <= right时,证明还有元素while (left < right){//求left和right的一个中间索引int middle = (left + right) >>> 1;//用中间索引的值和目标值进行比较if (target == a[middle]){//1.目标值 == 中间值,可以确定,找到了,返回middlereturn middle;}else if(a[middle] < target){//2.目标值大于中间值的情况下,可以确定,目标值在右边,left索引往右移left = middle + 1;}else {//3.目标值小于中间值的情况下,可以确定,目标值在左边,right索引往左移right = middle;}}//3.如果循环结束,没有找到,返回-1return -1;}public static void main(String[] args) {int[] a = {1,2,3,4,5,6,7,8,9};int target = 51;System.out.println("找到的场景:");for (int i = 0; i < a.length; i++){System.out.println("元素 " + a[i] + " 在数组中的位置为:" + binarySearchOne(a,a[i]));}System.out.println("\n没找到的场景:");System.out.println(target + " 在数组中的位置为:" + binarySearchOne(a,target));}
}注意事项:
代码优化
前面计算中间值middle时,用的计算公式是:int middle = (left + right) / 2;
但是这样写会出现怎么样的弊端呢?
当left+right计算出来的值已经 > int类型的范围时,结果就无法预估了,那算法的结果自然也是不对的。
那我们应该解决这个问题呢?
其实也很简单,通过位移运算符就可以了,每次往右移一位其实就是除以二,公式可以改为:int middle = (left + right) >>> 1;
总结
在前言中,我们通过几个示例对比了线性查找和二分查找,来引入二分查找的高效率,但由于数据量太小以及查找的位置来看,其实很片面,下面我们通过一种“事前分析法”的方式来对比一下两个算法。
那怎么判断一个算法的好坏呢?
一般是计算这个算法的最差的情况,那对于查找算法,最差的情况是不是就是找不到元素。首先,拆分前面两种算法每一行代码的执行次数。
线性查找法
拆分每一条语句的执行次数,假设元素个数是nint i = 0; 1次i < a.length; n+1次if (target == a[i]) n次i++ n次return -1 1次
将所有的执行次数相加,就是该算法的执行次数:3*n+3
二分查找法
那【二分查找法】的循环次数怎么确定呢?其实有一个规律:
元素个数 循环次数 规律
4-7 3次 log_2(4) + 1 = 2 + 1 = 3
8-15 4次 log_2(8) + 1 = 3 + 1 = 4
16-31 5次 log_2(16) + 1 = 4 + 1 = 5
32-63 6次 log_2(32) + 1 = 5 + 1 = 6
…… ……
从以上结果中,发现,元素个数和循环次数之间的规律为:log_2(n)(以2为底n的对数) + 1,
但由于元素个数是个区间,不能整除的向下取整,最终循环次数为 L = floor(log_2(n)) + 1下面拆分每一条语句的执行次数,假设元素个数是nint left = 0; 1次int right = a.length - 1; 1次while (left <= right) L + 1次int middle = (left + right) >>> 1; L次target == a[middle]; L次a[middle] < target; L次left = middle + 1; L次return -1; 1次
将所有的执行次数相加,就是该算法的执行次数:(floor(log_2(n)) + 1) * 5 + 4
算出来了两种算法的执行次数公式,下面取几个具体的数值带入n算一下。
假设n = 4:
线性查找算法:3*n+3 = 3*4+3=15
二分查找算法:(floor(log_2(n)) + 1) * 5 + 4 = (floor(log_2(4)) + 1) * 5 + 4 = 19
这么一看,好像线性查找更快一点,别急,我们在带入一个大一点的数:
假设n = 1024:
线性查找算法:3*n+3 = 3*1024+3=3075
二分查找算法:(floor(log_2(n)) + 1) * 5 + 4 = (floor(log_2(1024)) + 1) * 5 + 4 = 59
反转来了,当数据量不断增大的时候,二分查找的效率快非常多。
下面我们通过一个画来更直观的感觉,进入,Desmos | 图形计算器输入公式(n要换成x),可以看到二分查找是缓慢增加,而线性是直线增长。因此,可以得出结论,在一个有序的列表中查找数据,二分查找的执行效率远远高于线性查找。
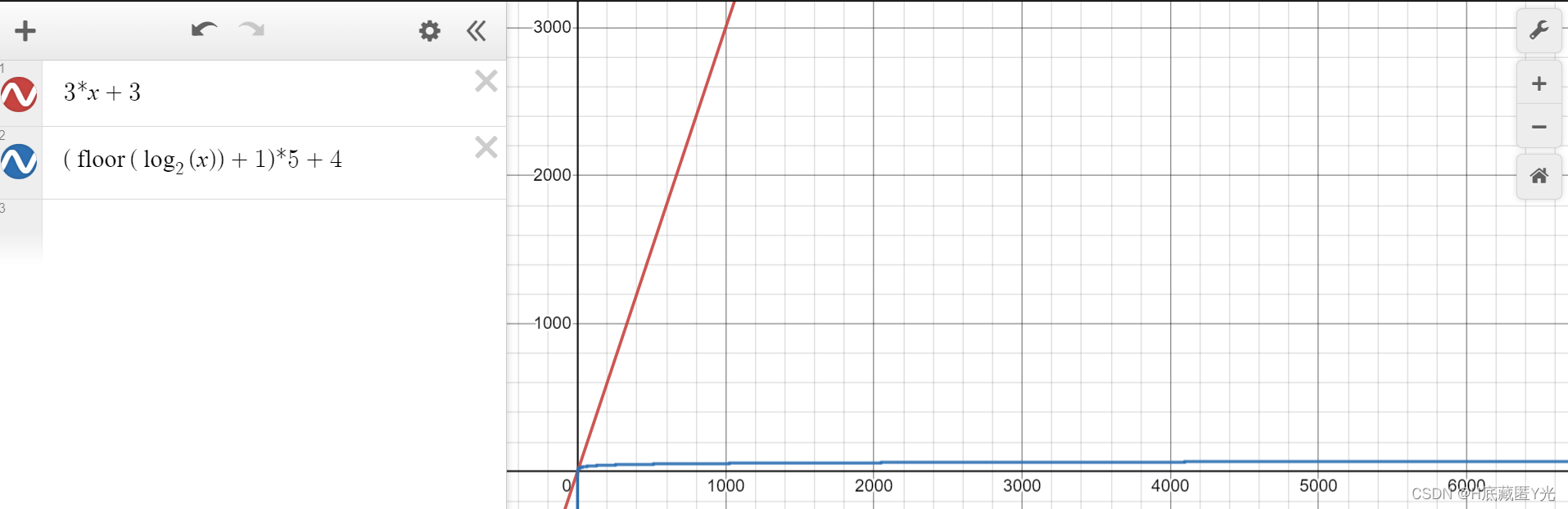




创建img对象不生效)


)










-SD图生图)
