大家好,我是前端西瓜哥。
最近遇到一个需求,给定一个多边形(边与边可能相交),求这个多边形的轮廓线。
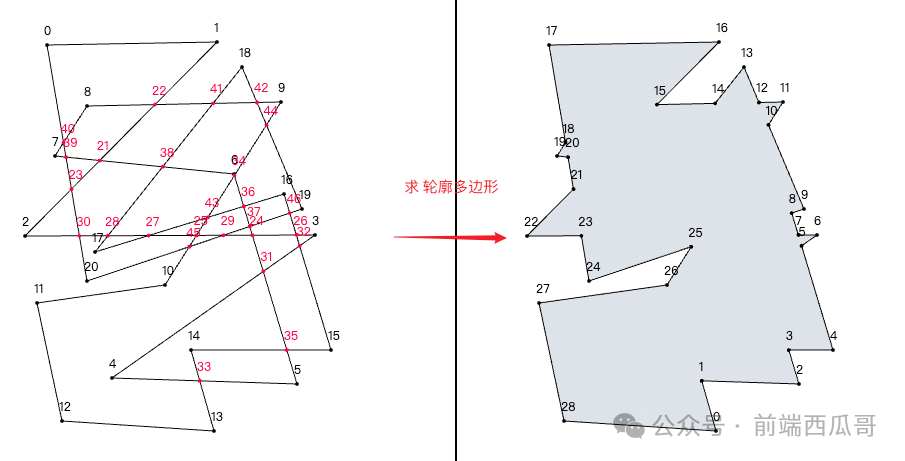
需要注意的是,轮廓线多边形内不能有空洞,使用的不是常见的非零绕数规则(nonzero)以及奇偶规则(odd-even)。
整体思路
-
计算多边形各边的交点,求出一个有多边形点和交点信息的邻接表。
-
从最下方的点开始,找出与其相邻节点中夹角最小的点保存到路径中,不断重复这个行为,直到点又回到起点位置。这里部分借鉴了凸包算法的其中一种叫做 Jarvis步进法 的解法。
原理很简单,就是代码太多,容易写错,需要多调试。
演示 demo
为了验证算法的正确性,我用 Canvas 写了个的简单交互 demo。
效果演示:
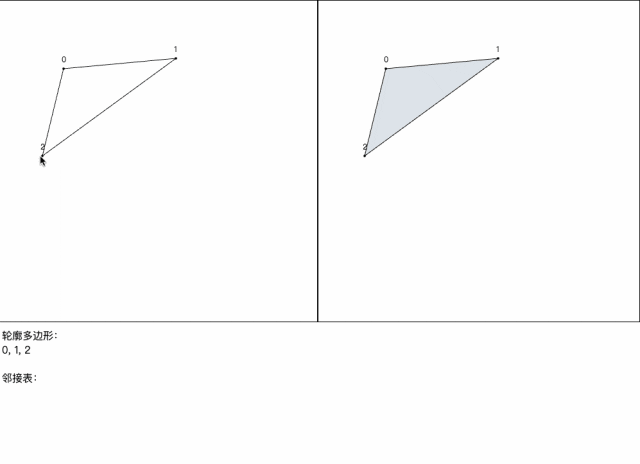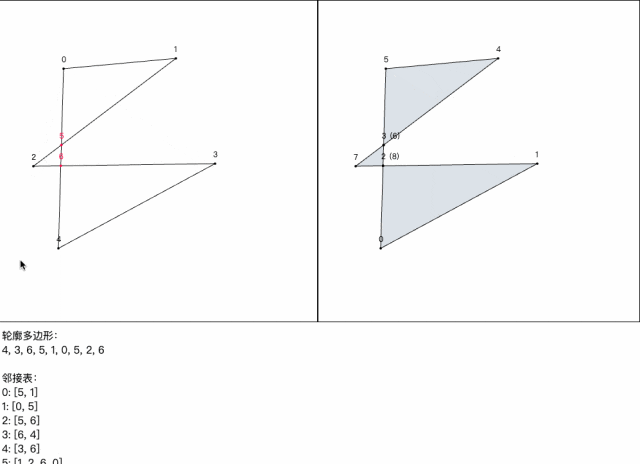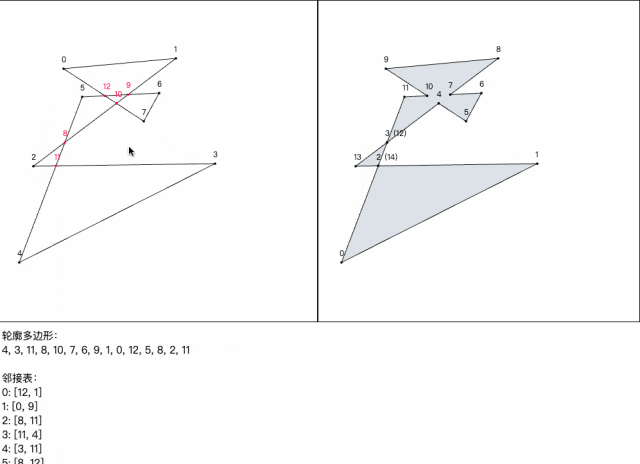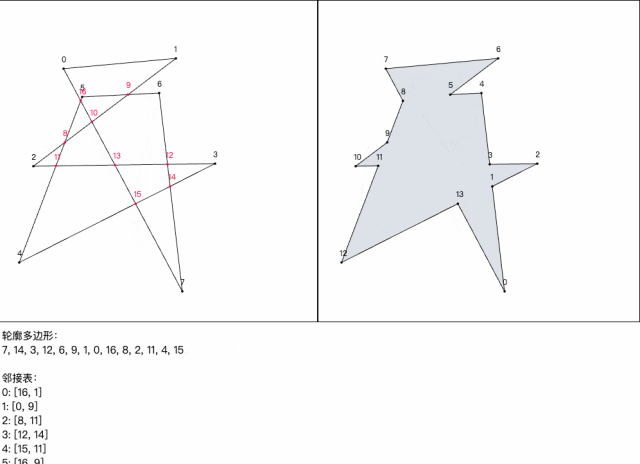
项目地址:
https://github.com/F-star/polygon-alg
Demo 地址:
https://f-star.github.io/polygon-alg/
下面我们看具体实现。
预处理
第一步是预处理。
目标多边形会使用点数组表示,比如:
const points = [{ x: 0, y: 0 },{ x: 6, y: 0 },{ x: 0, y: 10 },{ x: 6, y: 10 },
];
然后我们做去重,如果连续的多个点的位置 "相同",其实就等价于一个,保留一个就好。
不然后面找路径的时候,会出现零向量的计算导致报错。
function dedup(points: Point[]) {const newPoints: Point[] = [];const size = points.length;for (let i = 0; i < size; i++) {const p = points[i];const nextP = points[(i + 1) % size];if (p.x !== nextP.x || p.y !== nextP.y) {newPoints.push(p);}}return newPoints;
}
接着我们需要基于这个点数组,计算邻接表。
邻接表是一种表示图(Graph)的数据结构,记录每个点相邻的点有哪些。
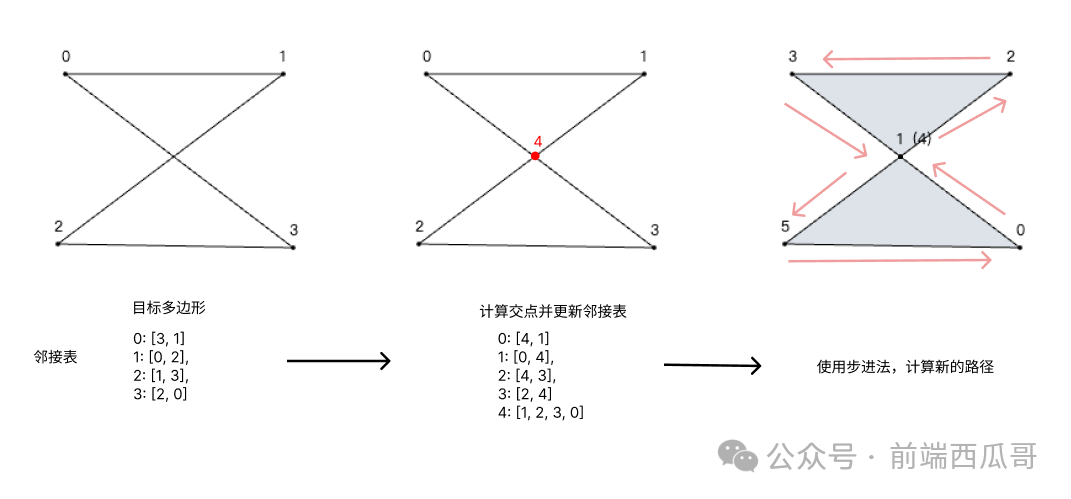
下面我们会以这个 “8” 字形多边形为例,进行讲解。
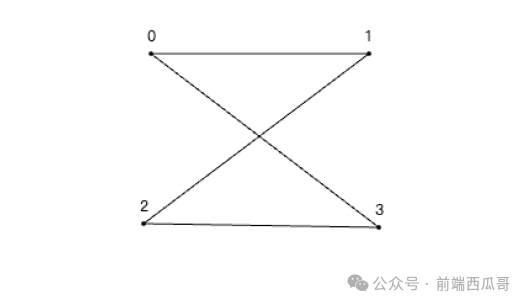
观察图示,可以得邻接表为:
[/* 0 */ [3, 1], // 表示 0 和 3、1 相连/* 1 */ [0, 2],/* 2 */ [1, 3],/* 3 */ [2, 0],
];
求初始邻接表的算法实现为:
// 求多边形的邻接表,size 为多边形点的数量
function getAdjList(size: number) {const adjList: number[][] = [];for (let i = 0; i < size; i++) {const left = i - 1 < 0 ? size - 1 : i - 1;const right = (i + 1) % size;adjList.push([left, right]);}return adjList;
}
需要求解的轮廓线多边形的点不一定是目标多边形上的点,也有可能是交点。
所以我们首先要做的是 求出目标多边形上的所有交点,并更新邻接表,得到一个额外带有交点信息的多边形邻接表。
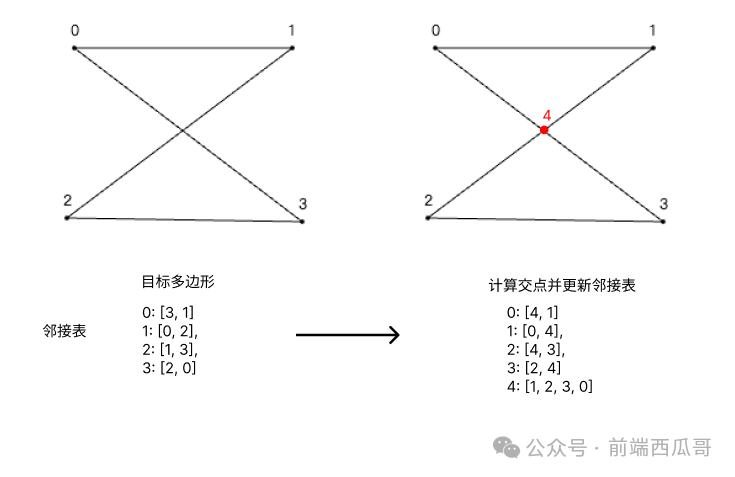
我们来看看具体要怎么实现。
求交点以及更新邻接表
这里需要一个求两线段交点的算法。刚好我写过,思路是解二元一次方程组,请看这篇文章:《解析几何:计算两条线段的交点》
用法为:
getLineSegIntersection({ x: 1, y: 1 }, { x: 4, y: 4 },{ x: 1, y: 4 }, { x: 4, y: 1 }
);
// { x: 2.5, y: 2.5 }
我们需要遍历多边形的所有边,计算其和其他不相邻边的交点。
const size = points.length;for (let i = 0; i < size - 2; i++) {const line1Start = points[i];const line1End = points[i + 1];let j = i + 2;for (; j < size; j++) {const line2EndIdx = (j + 1) % size;if (i === line2EndIdx) {// 相邻点没有计算交点的意义continue;}const line2Start = points[j];const line2End = points[line2EndIdx];const crossPt = getLineSegIntersection(line1Start,line1End,line2Start,line2End);// 找到一个交点if (crossPt) {// ... 更新邻接表// ...}}
}
为记录新的交点在哪四个点之间,我们要维护一个表。
它的 key 代表某条线段,value 为一个有序数组,记录落在该线段上的点,以及它们到线段起点的距离。该数组按距离从小到排序。
// [某条线]: [到线起点的距离, 在 points 中的索引值]
// 如:{ '2-3', [[0, 2], [43, 5], [92, 3]] }
const map = new Map<string, [number, number][]>();
线段 1-2 初始化时,表为
{‘1-2’: [[0, 1], // 点 1,距离起点 0[96, 2], // 点 2,距离起点 96]
}
边 1-2 和 3-0 计算得到一个交点(我们记为点 4)。把交点存到 crossPts 数组中。
接着求交点 4 在 1-2 中距离起点(即点 1)的距离,基于它判断落在 1-2 中哪两个点之间。结果是在点 1 和 点 2 之间,更新这两个点的邻接点数组,将其中的 1 和 2 替换为 5。
1: [0, 2] --> 1: [0, 4]
2: [1, 3] --> 2: [4, 3]
最后是更新 map 表:
{‘1-2’: [[0, 1], // 点 1,距离起点 0[0, 4], // 点 4,距离起点 40[96, 2], // 点 2,距离起点 96]
}
另一条相交边 3-0 同理。
代码实现:
// [某条线]: [到线起点的距离, 在 points 中的索引值]
// 如:{ '2-3', [[0, 2], [43, 5], [92, 3]] }
const map = new Map<string, [number, number][]>();
const crossPts: Point[] = [];
const size = points.length;// ...
if (crossPt) {crossPts.push(crossPt);const crossPtAdjPoints: number[] = [];const crossPtIdx = size + crossPts.length - 1;/************ 计算 line1Dist 并更新 line1 两个点对应的邻接表 ********/{const line1Key = `${i}-${i + 1}`;if (!map.has(line1Key)) {map.set(line1Key, [[0, i],[distance(line1Start, line1End), i + 1],]);}const line1Dists = map.get(line1Key)!;// 计算相对 line1Start 的距离const crossPtDist = distance(line1Start, crossPt);// 看看在哪两个点中间const [_left, _right] = getRange(line1Dists.map((item) => item[0]),crossPtDist);const left = line1Dists[_left][1];const right = line1Dists[_right][1];crossPtAdjPoints.push(left, right);// 更新邻接表const line1StartAdjPoints = adjList[left];replaceIdx(line1StartAdjPoints, left, crossPtIdx);replaceIdx(line1StartAdjPoints, right, crossPtIdx);const line1EndAdjPoints = adjList[right];replaceIdx(line1EndAdjPoints, left, crossPtIdx);replaceIdx(line1EndAdjPoints, right, crossPtIdx);// 更新 map[line1Key] 数组line1Dists.splice(_right, 0, [crossPtDist, crossPtIdx]);}/************ 计算 line2Dist 并更新 line2 两个点对应的邻接表 ********/{const line2Key = `${j}-${line2EndIdx}`;// ...这里和上面一样的,读者感兴趣可以把这两段代码复用为一个方法}// 更新邻接表adjList.push(crossPtAdjPoints);
}
步进法找路径
上面我们得到了带交点的多边形邻接表,必要的点的数据都准备好了,下一步就是一从一个点出发走出一条多边形的路径。
(1)取左下角点作为起点
找顶点(不包括交点)中最靠下的点,如果有多个,取最靠左的。这个点一定是轮廓多边形的一个点。
(2)步进,取角度最小的邻接点为路径的下一个点
计算当前点到上一个点的向量,和当前点到其他邻接点相邻点向量逆时针夹角。找出其中夹角最小的邻接点,作为下一个点,不断步进,直到当前点为路径起点。
对于起点,它没有前一个点,用一个向右向量 (1, 0) 参与计算。
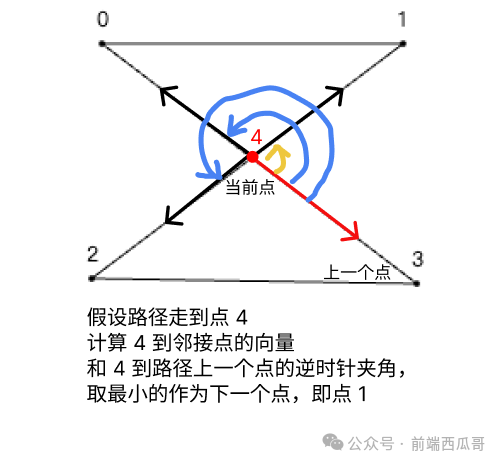
const allPoints = [...points, ...crossPts];// 1. 找到最下边的点,如果有多个 y 相同的点,取最左边的点
let bottomPoint = points[0];
let bottomIndex = 0;
for (let i = 1; i < points.length; i++) {const p = points[i];if (p.y > bottomPoint.y || (p.y === bottomPoint.y && p.x < bottomPoint.x)) {bottomPoint = p;bottomIndex = i;}
}const outlineIndices = [bottomIndex];// 2. 遍历,找逆时针的下一个点
const MAX_LOOP = 9999;
for (let i = 0; i < MAX_LOOP; i++) {const prevIdx = outlineIndices[i - 1];const currIdx = outlineIndices[i];const prevPt = allPoints[prevIdx];const currPt = allPoints[currIdx];const baseVector =i == 0? { x: 1, y: 0 } // 对于起点,它没有前一个点,用向右的向量: {x: prevPt.x - currPt.x,y: prevPt.y - currPt.y,};const adjPtIndices = adjList[outlineIndices[i]];let minRad = Infinity;let minRadIdx = -1;for (const index of adjPtIndices) {if (index === prevIdx) {continue;}const p = allPoints[index];const rad = getVectorRadian(currPt.x, currPt.y, p.x, p.y, baseVector);if (rad < minRad) {minRad = rad;minRadIdx = index;}}if (minRadIdx === outlineIndices[0]) {break; // 回到了起点,结束}outlineIndices.push(minRadIdx);
}
if (outlineIndices.length >= MAX_LOOP) {console.error(`轮廓多边形计算失败,超过最大循环次数 ${MAX_LOOP}`);
}// outlineIndices 为我们需要的轮廓线多边形
这里有个求两向量夹角的方法要实现,这里不具体展开了。
简单来说就是通过点积公式计算夹角,但夹角只在 0 到 180 之间,这里需要再利用叉积的特性判断顺时针还是逆时针,将顺时针的夹角用 360 减去。
结尾
算法的整体思路大概就是这样。
这里有几个优化点。
首先判断大小的场景可进行优化,比如求距离时使用了开方,其实没必要开方。
因为 a^2 < b^2 是可以推导出 a < b 的,所以可直接对比距离的平方,我这里是为了让读者方便理解,故意简化了。对比夹角的大小同理,可改为对比投影加夹角方向。
此外还有一些边缘情况没有测试和处理。
比如多个交点的位置是 “相同” 的,最好做一个合并操作(否则在一些非常特定的场景可能会有问题)。
我是前端西瓜哥,欢迎关注我,学习更多平面解析几何知识。

)




![[深度学习]yolov9+deepsort+pyqt5实现目标追踪](http://pic.xiahunao.cn/[深度学习]yolov9+deepsort+pyqt5实现目标追踪)
)








)


