【数据结构初阶 6】二叉树：堆的基本操作 + 堆排序的实现

文章目录

🌈 Ⅰ 二叉树的顺序结构
🌈 Ⅱ 堆的概念与性质
🌈 Ⅲ 堆的基本操作
- 01. 堆的定义
- 02. 初始化堆
- 03. 堆的销毁
- 04. 堆的插入
- 05. 向上调整堆
- 06. 堆的创建
- 07. 获取堆顶数据
- 08. 堆的删除
- 09. 向下调整堆
- 10. 判断堆空
🌈 Ⅳ 堆的基本应用
- 01. 堆排序的实现
- 02. TOP K 问题

🌈 Ⅰ 二叉树的顺序结构

1. 顺序存储结构概念

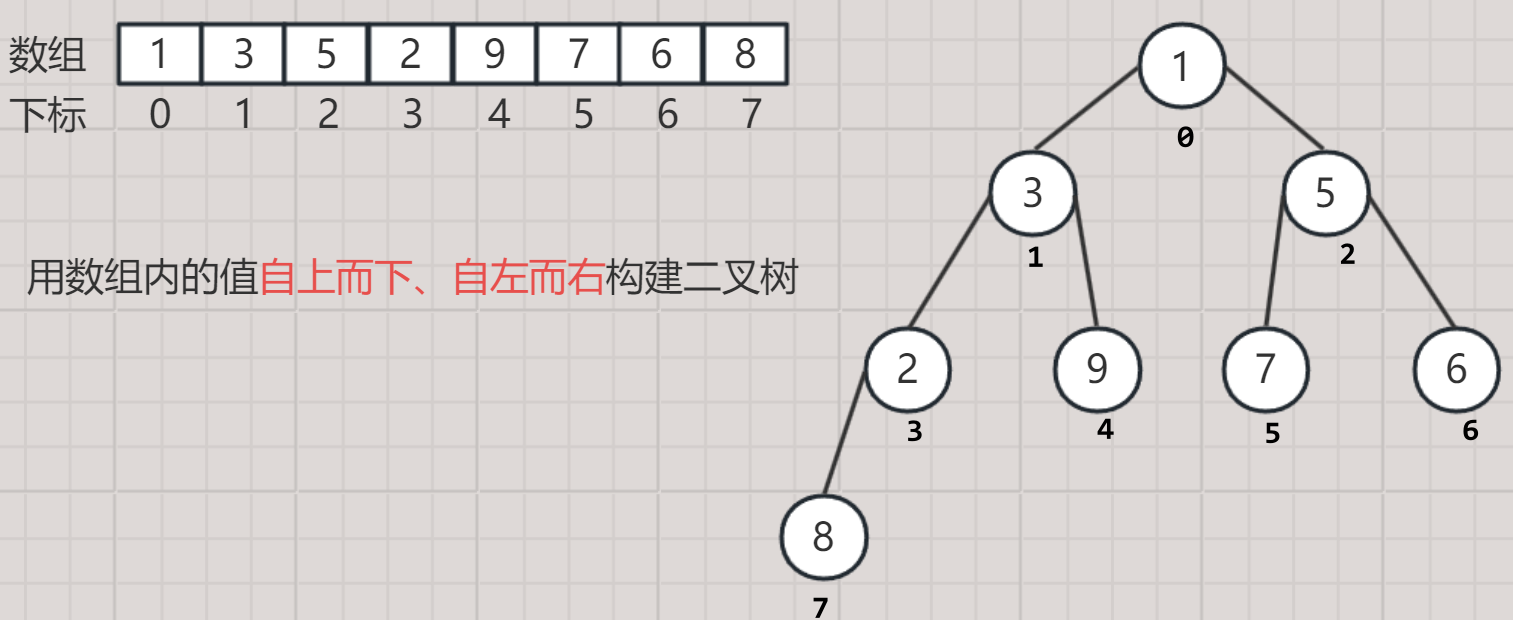
顺序存储结构就是使用数组来存储二叉树的数据。
这种结构下的逻辑结构是二叉树，物理结构是数组。
数组内的值是将二叉树自上而下、自左而右依次存储，反过来数组构建二叉树也是这个顺序。

2. 顺序存储结构优势

使用这种结构可以很容易得出父子结点的下标。

双亲结点下标 = ( 左或右孩子结点下标 - 1 ) / 2
左孩子结点下标 = 双亲结点下标 * 2 + 1
右孩子结点下标 = 双亲结点下标 * 2 + 2

3. 适合顺序存储的二叉树

只有满二叉树或完全二叉树这种能够有效利用数组空间，适合使用顺序存储。

🌈 Ⅱ 堆的概念与性质

1. 堆的概念

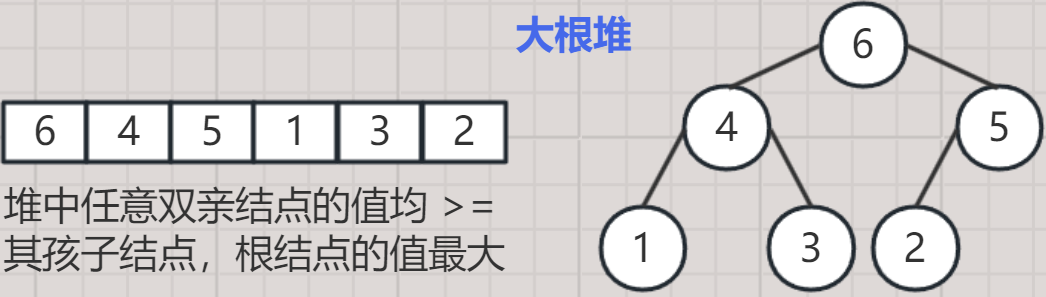
将一组数据构建成一棵完全二叉树，如果根节点的值大于 / 小于左右子树的所有值，则称该完全二叉树为一个堆。
将根节点最大的堆称做大根堆；将根节点最小的堆称为小根堆。

2. 堆的性质

堆总是一棵完全二叉树。
有序数组一定是堆，反之却不一定。
小根堆：堆中所有双亲结点的值总是 <= 其孩子结点，根结点的值最小。
大根堆：堆中所有双亲结点的值总是 >= 其孩子结点，根结点的值最大。

🌈 Ⅲ 堆的基本操作

01. 堆的定义

堆在计算机看来实际就是个数组，但不能只用数组表示堆，还需要记录下每个堆的有效数据个数以及对应堆的容量。
因此就要建立一个堆的结构体来管理每个堆。

typedef int HPDataType;	// 堆中每个结点的数据类型typedef struct Heap		
{int size;			// 记录数组中有效数据个数int capacity;		// 记录开辟的数组空间大小HPDataType* data;	// 为堆空间开辟的数组
}Heap;

注意：因为 size 是用来记录堆中有效数据的个数，因此 size 天生是最后一个有效数据的后一个位置的下标。

02. 初始化堆

void HeapInit(Heap* hp)
{assert(hp);hp->data = NULL;hp->size = hp->capacity = 0;
}

03. 堆的销毁

void HeapDestory(Heap* hp)
{assert(hp);free(hp->data);hp->data = NULL;hp->size = hp->capacity = 0;
}

04. 堆的插入

堆的本质实际上是个数组，因此往堆中插入数据就将数据尾插到数组中。
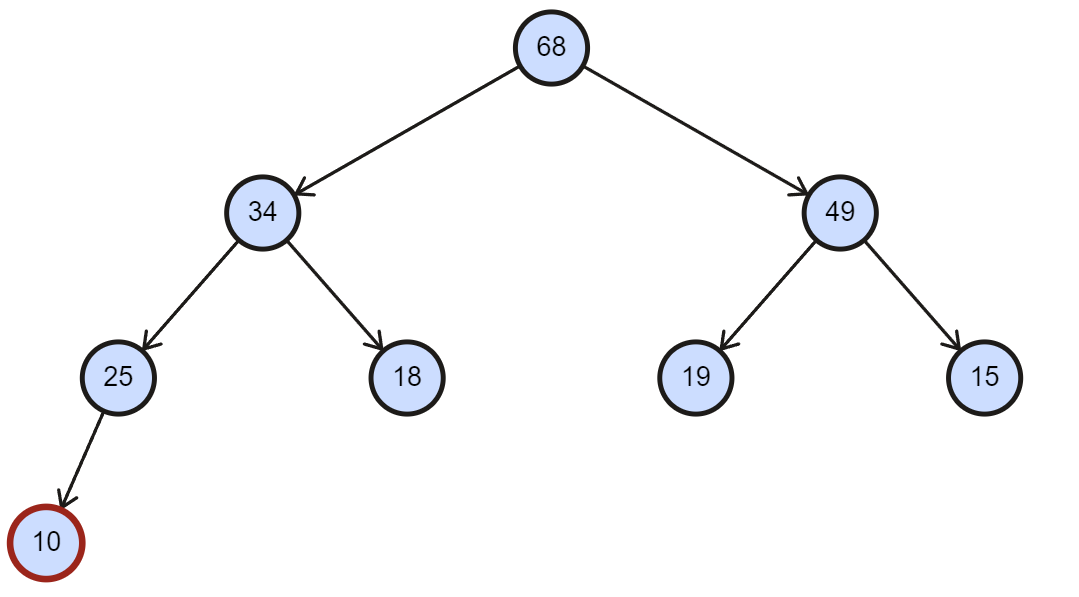
当前有一组数据为 [68, 34, 49, 25, 18, 19, 15] 的数组构成的大根堆，往最后插入一个 10。

void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->capacity == hp->size)		//是否要扩容{int newcapacity = hp->capacity = 0 ? 4 : 2 * hp->capacity;HPDataType* tmp = (HPDataType*)realloc(hp->data, newcapacity * sizeof(HPDataType));assert(tmp);hp->capacity = newcapacity;hp->data = tmp;}hp->data[hp->size++] = x;			//插入新数据AdjustUp(hp->data, hp->size - 1);	//堆向上调整
}

05. 向上调整堆

1. 为何要向上调整堆

插入数据之后可能导致破坏堆的结构，可能要对堆进行调整。
往一个堆中插入不同的值时，需要判断会不会破会堆的结构。
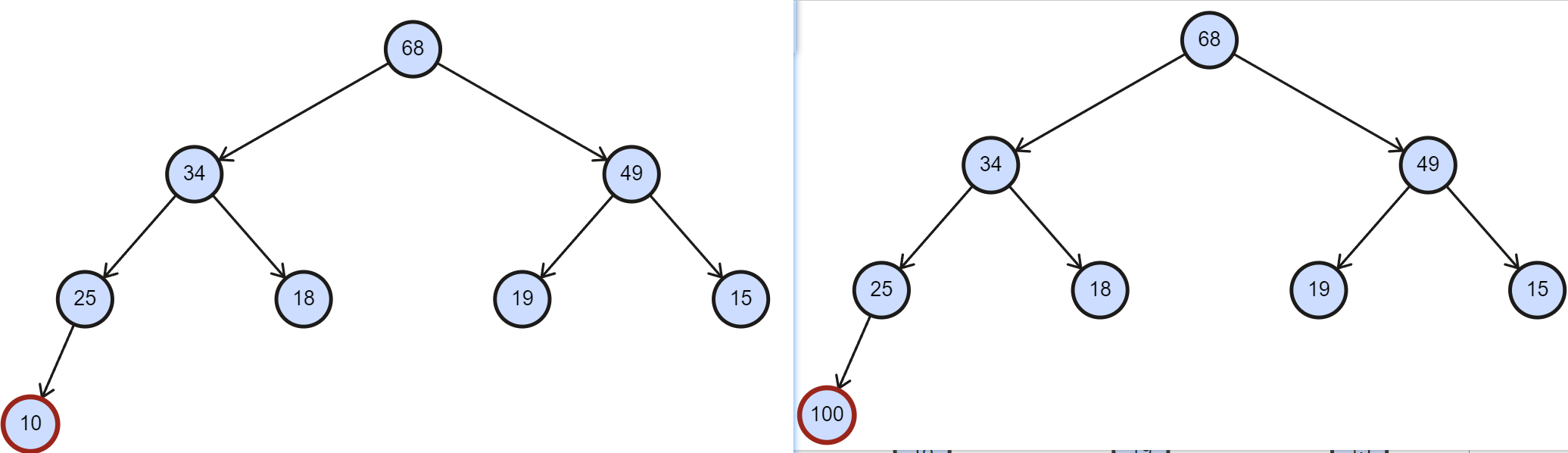
- 下图中，插入了 10 不会破坏大根堆，插入 100 却会。

2. 根据堆的性质判断是否要调堆

小根堆中：只需要判断新插入的数据是否 < 其双亲结点的值，如果是则和其双亲结点交换。
大根堆中：只需要判断新插入的数据是否 > 其双亲结点的值，如果是则和其双亲结点交换。
在交换了之后，新结点可能比它双亲的双亲还小 / 大，要一直交换到符合堆的定义为止。
- 新结点 100 和它的双亲交换之后还是大于其新的双亲，要交换到符合堆定义为止。
如下图所示的将 100 向上调整到它最终位置，即为堆的向上调整。

3. 堆的向上调整实现思路

定义的函数形参 data 是一个存储堆中数据的数组，child 是新插入的结点的下标。
算出新结点的双亲结点，然后与其双亲结点比较，如果不符合大 / 小根堆的定义则交换。
交换了之后原来双亲结点的位置就变为了新结点的位置，再算出该结点新的双亲结点去比较。
当将新结点向上调整到符合大 / 小根堆的定义时停止调整，最坏情况新结点会被调成根结点。

4. 堆的向上调整代码实现

该代码适用于调成大 / 小根堆。

void AdjustUp(HPDataType* data, int child)		// 向上调整堆
{int parent = (child - 1) / 2;				// 算出新结点的双亲结点while (child > 0)							// 最坏情况新结点会被调成根结点{// if (data[child] < data[parent])		// 按照 小根堆 定义向上调整if (data[child] > data[parent])			// 按照 大根堆 定义向上调整{swap(&data[child], &data[parent]);	// 交换双亲和孩子结点的数据child = parent;						// 原双亲结点的位置给了新结点parent = (parent - 1) / 2;			// 求新结点双亲的双亲的位置}else									// 结点被调到符合 大/小 根堆{break;								}}
}

06. 堆的创建

实现思路

将一组数据从第一个开始依次进堆，每放一个数据进堆就调用一次向上调整算法。
- 当前有一组数据，将它们依次插入进堆，然后调用向上调整算法。

代码实现

int main()
{int test[] = {85,9,1,7,6,7,5,45,13,54};size_t size = sizeof(test) / sizeof(test[0]);Heap hp;HeapInit(&hp);// 将 test 数组内的值依次插入进堆for (int i = 0; i < size; i++){HeapPush(&hp, test[i]);}return 0;
}

07. 获取堆顶数据

数组的 0 号位置就是堆顶元素，直接返回该位置的值即可。

HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->size > 0);	// 堆中有元素可被获取return hp->data[0];		// 堆中结点的值不一定是 int 类型
}

08. 堆的删除

堆的删除规定删除根结点的数据，即删除堆顶结点。

实现思路

将堆顶元素和堆尾元素交换，然后将堆中有效数据个数 -1 即可实现删除。

代码实现

void HeapPop(Heap* hp)
{assert(hp);assert(hp->size > 0);							// 堆中有元素swap(&hp->data[0], &hp->data[hp->size - 1]);	// 堆顶和堆尾互换hp->size--;										// 删除最后一个元素AdjustDown(hp->data, hp->size, 0);				// 将堆顶元素向下调整
}

09. 向下调整堆

1. 为何要向下调整堆

某些情况下，堆中的某一个非叶子结点可能要比其孩子结点大 / 小，不符合小 / 大根堆的定义。
- 如上图：将 9 换到根结点之后明显就破坏了大根堆的结构，要将其向下调整到合适位置。

2. 向下调整实现思路

比较要下沉的结点 k 的左右孩子的值，找出值较大 / 小的那个孩子出来。
如果是大根堆，就用最大孩子和 k 互换；如果是小根堆，就用最小孩子和 k 互换。
重复上述步骤，直到将 k 调到它应在的位置即可。

3. 向下调整代码实现

按照小根堆的定义向下调整

void AdjustDown(HPDataType* data, int size, int parent)
{int child = parent * 2 + 1;	// 假设是结点的左孩子比较小while (child < size)		// 不能超过数组的范围{// 如果右孩子 < 左孩子，则最小孩子结点换成右孩子if (child + 1 < size && data[child + 1] < data[child]){child++;}//最小孩子结点 < 其双亲结点则要交换if (data[child] < data[parent]){swap(&data[child], &data[parent]);child = child * 2 + 1;parent = parent * 2 + 1;}else{break;}}
}

按照大根堆的定义向下调整，将两个 if 里用于比较左右孩子大小的 < 换成 > 即可。
- 第一个 if：将 data[child + 1] < data[child] 换成 data[child + 1] > data[child]
- 第二个 if：将 data[child] < data[parent] 换成 data[child] > data[parent]

void AdjustDown(HPDataType* data, int size, int parent)
{int child = parent * 2 + 1;	// 假设是结点的左孩子比较大while (child < size)		// 不能超过数组的范围{// 如果右孩子 > 左孩子，则最大孩子结点换成右孩子if (child + 1 < size && data[child + 1] > data[child]){child++;}//最大孩子结点 > 其双亲结点则要交换if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = child * 2 + 1;parent = parent * 2 + 1;}else{break;}}
}

10. 判断堆空

判断堆中有效数据的个数是否为 0 即可。

int HeapEmpty(Heap* hp)
{assert(hp);return 0 == hp->size;
}

🌈 Ⅳ 堆的基本应用

01. 堆排序的实现

排序思路

事先声明：排升序用大根堆，排降序用小根堆 (默认为升序)

将待排序的 n 个数据使用向下调整造成一个大根堆，此时堆顶就是整个数组的最大值。
将堆顶和堆尾互换，此时堆尾的数就变成了最大值，剩余的待排序数组元素个数为 n - 1 个。
将剩余的 n - 1 个数调整回大根堆，将新的大根堆的新的堆顶和新的堆尾互换。
重复执行上述步骤，即可得到有序数组。

举个例子

当前有数据为 [ 8, 9, 4, 74, 12, 15, 6 ] 现对其进行升序排序，要先构成大根堆。

代码实现

data 指向原数组空间，n 表示要排序的数据个数。

// 排成升序
void HeapSort(int* data, int n)
{int i = 0;int end = n - 1;// 从最后一个非叶子结点开始依次往前向下调整构建大根堆// n - 1 是最后一个结点的下标，(n - 1 - 1) / 2 是最后一个结点的夫结点下标// 也就是最后一个非叶子结点for (i = (n - 1 - 1) / 2; i >= 0; i--){// 要使用建大堆的向下调整算法AdjustDown(data, n, i);}// 0 和 end 夹着的是待排序数据，end 是待排序数据的个数// 每次都选出一个最大的数放到 end 处，然后待排序数据个数 end - 1while (end > 0){swap(&data[0], &data[end]);	// 互换堆顶和堆尾的数据AdjustDown(data, end, 0);	// 从根位置 (0) 开始的向下调整end--;						// 缩小待排序数据区间，且个数 - 1}
}

02. TOP K 问题

问题概述

在 n 个数中找出最大 / 最小的前 k 个数 (前提：n 远大于 k)

实现思路

用这 n 个数的前 k 个数来构建一个堆，这个堆就只有 k 个数。
- 求前 k 个最大的元素，就建小根堆。
- 求前 k 个最小的元素，就建大根堆。
用剩余的 n - k 个元素依次与堆顶元素比较。
- 求前 k 个最大的元素，就用比小根堆顶大的数和其互换，然后向下调整堆。
- 求前 k 个最小的元素，就用比大根堆顶小的数和其互换，然后向下调整堆。

举个栗子

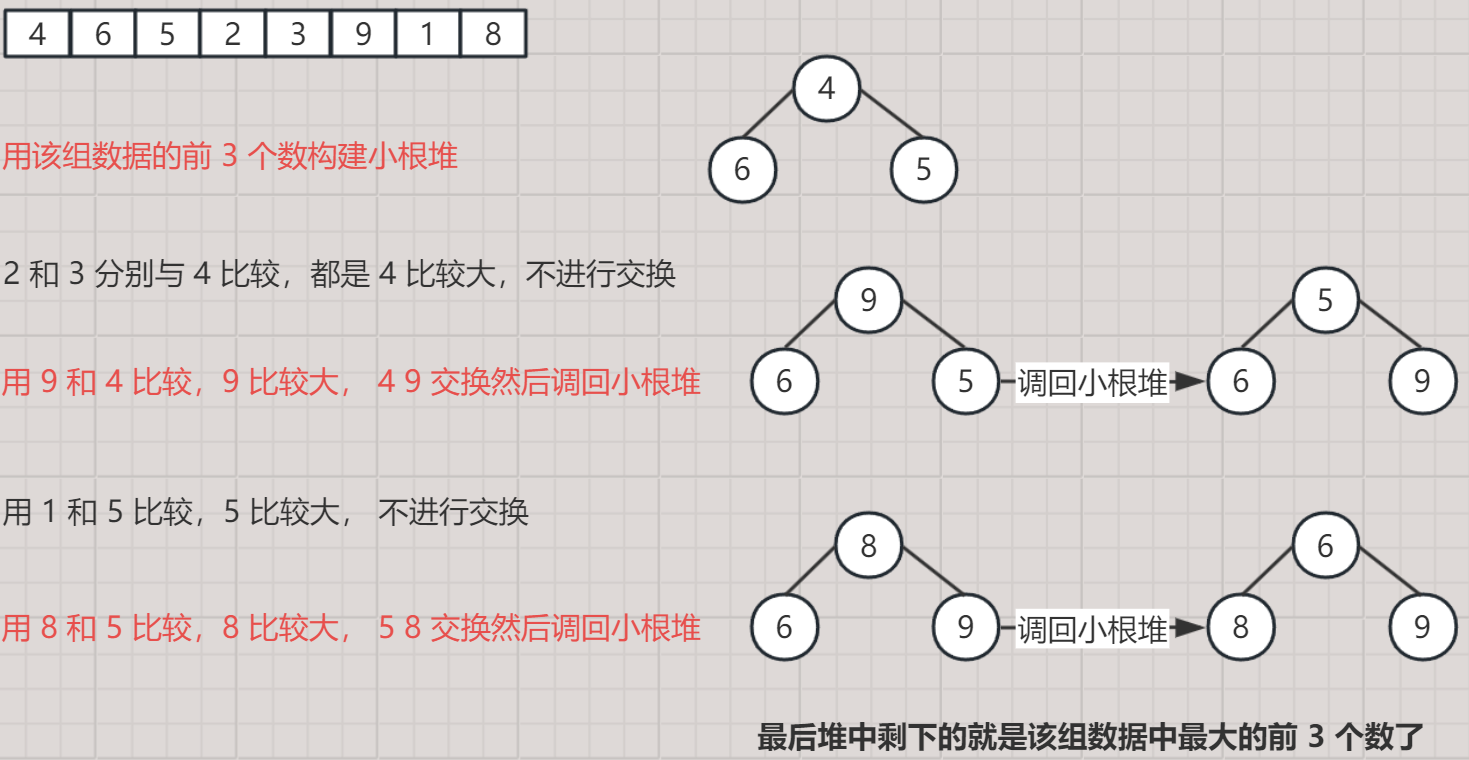
当前有如下一组数据，现求其最大的前 3 个数
- [ 4, 6, 5, 2, 3, 7, 9, 1, 8 ]
建成小堆能将后面比堆顶小的数全部挡在外面，最后堆中剩下的 3 个值就是最大的那三个。

代码实现

void TopK(int* data, int n, int k)
{int i = 0;int j = 0;HPDataType* MinHeap = (HPDataType*)malloc(sizeof(HPDataType) * k);assert(MinHeap);for (i = 0; i < k; i++)				// 将前 k 个数先插入进堆中{MinHeap[i] = data[i];}for (i = (k - 2) / 2; i >= 0; i--)	// 将这 k 个数的堆向下调整成小根堆{AdjustDown(MinHeap, k, i);}for(j = k; j < n; j++)				// 将 k 之后的数据依次和堆顶比较{if (MinHeap[0] < data[j])		// 后续数据大于堆顶则和堆顶互换后调整{MinHeap[0] = data[j];AdjustDown(MinHeap, k, 0);}}
}