目录
1.Cache的原理
2.Cache的性能
3.Cache和主存的映射方式
(1)全相联映射
(2)直接映射
(3)组相联映射
4.替换算法
(1)随机算法(RAND)
(2)先进先出算法(FIFO)
(3)近期最少使用(LRU)
(4)最近不经常使用(LFU)
5.Cache写策略
(1)写命中
•写回法
•全写法
(2)写不命中
•写分配法
•非写分配法
补充:
1.Cache的原理
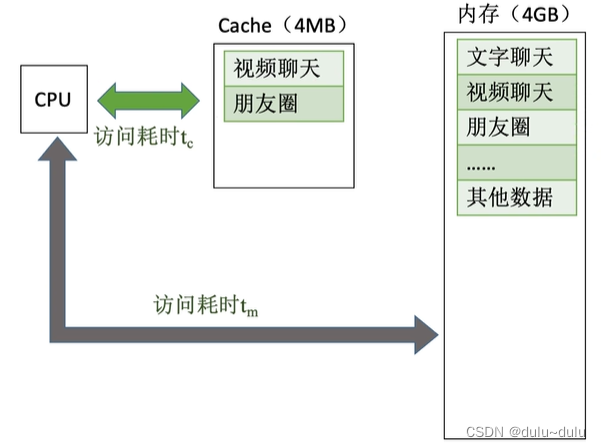
Cache被继承在CPU内部,用SRAM实现,速度快,集成度低(在芯片大小不能很大的情况下,Cache被允许的存储空间非常小),成本高
基于局部性原理,不难想到,可以把CPU目前访问的地址“周围”的部分数据复制到cache中,当CPU想访问这些数据时,直接到Cache中寻找即可,提高了CPU的运行速度。
对于局部性原理的说明:
如下图所示,二维的数组会在内存中被顺序存放,若现在访问的是a[0][0]数组,那么与其相邻的数组可能很快会被访问,这就是空间局部性
空间局部性:在最近的未来要用到的信息(指令和数据),很可能与现在正在使用的信息在存储空间上是邻近的
时间局部性:在最近的未来要用到的信息,很可能是现在正在使用的信息,例如循环结构的指令代码。
若把程序A改为程序B,即按列访问,那么其访问二维数组的顺序为a[0][0],a[1][0],a[2][0]
可以发现,程序B空间局部性更差一些。
2.Cache的性能
CPU先访问Cache,若Cache未命中再访问主存,设为CPU访问一次Cache所需时间,
为CPU访问一次主存所需时间。若CPU想要访问的信息已在Cache中,那么称为CPU命中,命中率为H,那么缺失(未命中)率M=1-H
那么系统的平均访问时间t为:
若CPU同时到Cache和主存中找需要的数据,若在Cache中命中,若Cache命中,则立即停止访问主存,那么访问的时间为,若Cache未命中,由于是同时查找,那么访问的时间为
,那么总公式为:
例如:
假设Cache的速度是主存的5倍,且Cache的命中率为95%),则采用cache后,存储器性能提高多少(设Cache和主存同时被访问,若cache命中则中断访问主存)?
若Cache和主存同时访问,命中时访问时间为t,未命中时访问时间为5t
平均访问时间为 0.95xt + 0.05x5t = 1.2t故性能为原来的 5t/1.2t
4.17倍
若先访问Cache再访问主存,命中时访问时间为t,未命中时访问时间为t+5t
平均访问时间为T
=0.95xt + 0.05x6t = 1.25t
故性能为原来的5t/1.25t = 4倍
基于局部性原理,不难想到,可以把CPU目前访问的地址“周围”的部分数据放到Cache中。如何界定“周围”?
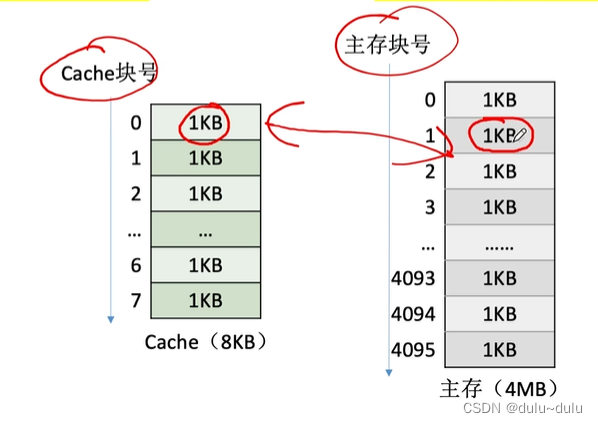
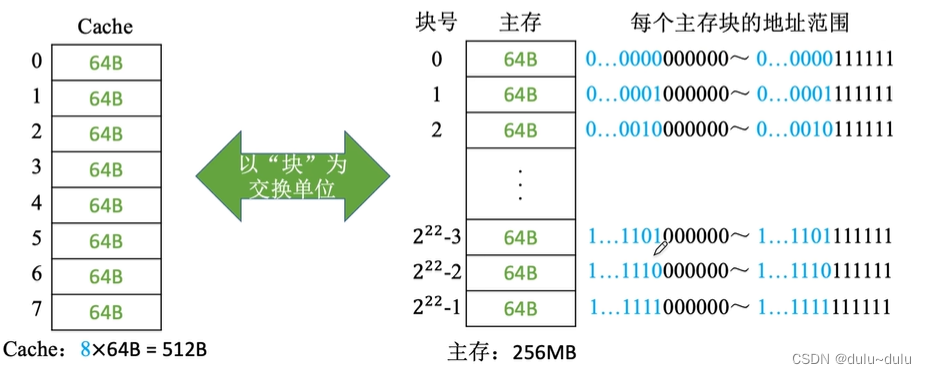
可以将主存的存储空间“分块”,如:每 1KB为一块。主存与Cache之间以“块”为单位进行数据交换
在CPU访问某个内存数据时,可以通过其地址信息判断他属于哪一个块,并且把这一块复制到Cache中
如图所示,主存容量为4MB(2^22),每一块为1K(2^10),那么整个主存被分为2^12=4096块
所以主存的地址共22位,结构如下:
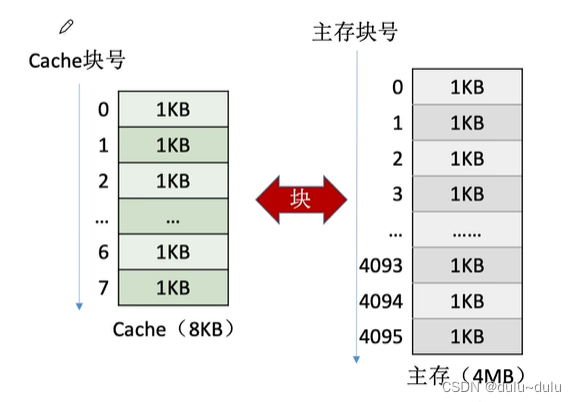
同理,我们将Cache分为大小相同的块,那么主存与Cache就能进行以“块”为单位的数据交换
注:操作系统中,通常将主存中的“一个块”也称为”一个页/页面/页框”,Cache中的“块”也称为“行”
3.Cache和主存的映射方式
CPU如何区分Cache和主存的数据块的对应关系?
CPU先访问Cache,再访问内存,并将内存相应的块数据复制到Cache中(不是将其从内存中删除) ,即每次被访问的主存块一定会被立即调入Cache,那么如何记录主存块与Cache块的映射关系呢?
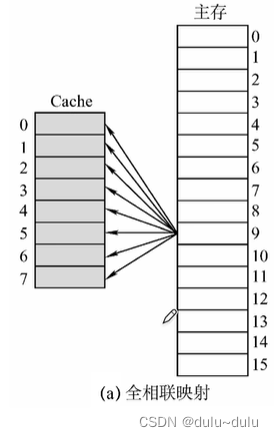
(1)全相联映射
主存块可以放在Cache的任意位置
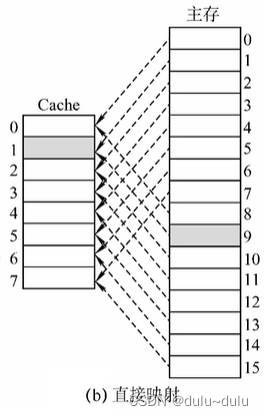
(2)直接映射
每个主存块只能放到一个特定的位置:Cache块号=主存块号%Cache总块数
例如主存块号为1,9的内存块都会被放到Cache块号为1的位置。
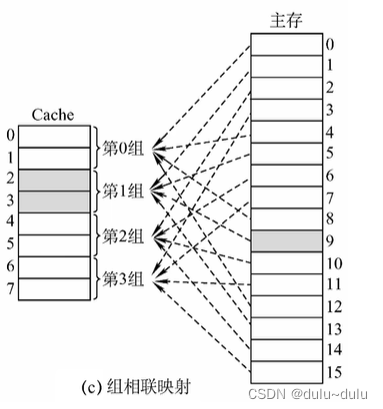
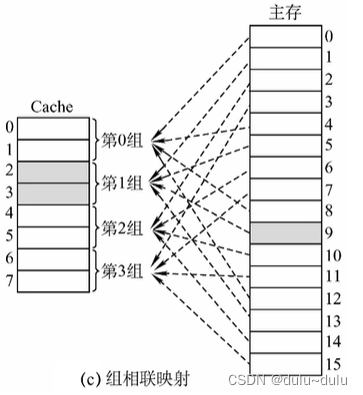
(3)组相联映射
将Cache的各个块进行分组,每个分组的总块数相同,每个主存块可放到特定分组中的任意一个位置:组号=主存块号%分组数
例如下图中Cache被分为4个分组,那么对于内存块号为1的内存块就是1%4=1,那么1号内存块就会被放在Cache中第1组的任意空闲位置。
我们回到最初的问题:CPU如何区分Cache和主存的数据块的对应关系呢?
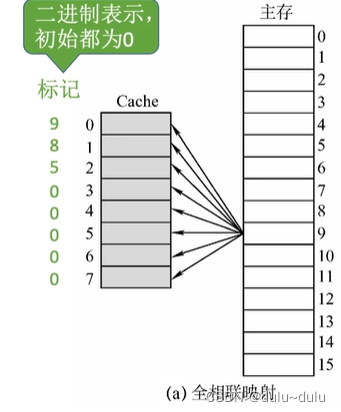
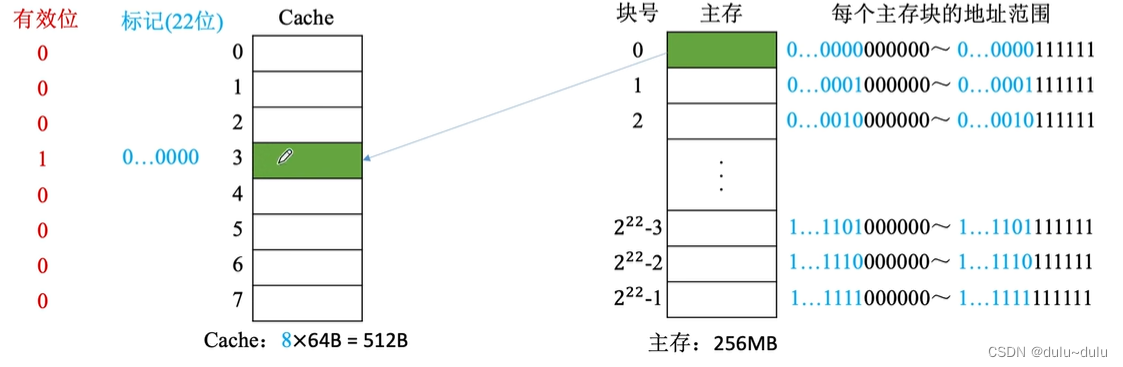
可以给每个cache块增加一个“标记”记录对应的主存块号,例如0号Cache块的标记为9,则表示0号Cache块的数据是9号内存块的副本
若2进制表示,初始都为0,没有数据的则记为0,但是0也可以表示为是主存号为0的内存块的副本,所以光有标记不行,还需要增加有效位
有效位的1表示有效,0表示无效,如下图所示,只有7号Cache块标记为0,有效位为1,表示7号Cache块存储的是0号内存块的副本,其余标记为0的Cache块,则表示没有数据
对于全相联映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行(即Cache块,与主存快的大小相等),行长为64B。
256M=2^28主存的地址,共28位,
按照如上结构,给定主存地址如下所示:
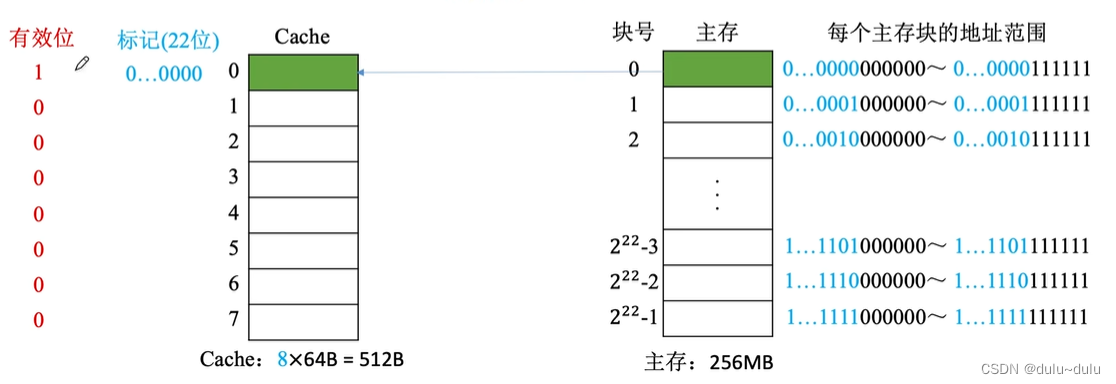
全相联映射的过程,全相联映射中,主存块可以放到Cache中的任意一个位置,如下图所示,主存块映射到3号Cache块,首先会将其有效位置1,接着标记其映射的是主存的哪一位置,即标记主存块号(22位)
若CPU需要访问主存地址1.....1101001110:
①CPU会将主存地址的前22位,对比Cache中所有块的标记;
②若标记匹配且有效位=1,则Cache命中,在Cache中访问块内地址为001110的单元
③若未命中或有效位=0,则正常访问主存
优点:Cache存储空间利用充分命中率高;
缺点:查找“标记”最慢,有可能需要对比所有行的标记
对于直接映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行,行长为64B。
直接映射,主存块在Cache中的位置=主存块号%Cache总块数例如,对于0号内存块,只能放到0%8=0,即0号Cache块,将有效位改为1,同时标记为0...0000(22位)
若想将8号内存块调入Cache,8%8=0,则需要将之前存放的数据覆盖,同时要把标记改为8号主存块的块号0...01000
所以,如果采用直接映射的方式,虽然其他地方有空闲的Cache块,但是8号主存块不能使用
相比于全相联映射,直接映射灵活性低,空间利用率也不充分
是否能优化标记呢?
对于上图Cache块数为8,主存块号%2^3,相当于留下主存块号最后3位二进制数,表示主存块在Cache中的位置,也就是说某一主存块能够存放在0号 Cache,那么这个主存块的块号的末尾三位一定是000
我们已经知道主存块放在Cache中的位置,就没必要记录末尾3位了,将主存块号的其余位作为标记即可(标记保留19位即可,即块号的前19位)
总结:
若Cache总块数=2^n,则主存块号末尾n位直接反映它在Cache中的位置,将主存块号的其余位作为标记即可
基于这种方式,CPU如何访问主存地址:
若CPU访问主存地址0...01000 001110:
①根据主存块号的后3位确定Cache行
②若主存块号的前19位与Cache标记匹配且有效位=1,则Cache命中,在Cache块中访问块内地址为001110的单元。
③若未命中或有效位=0,则正常访问主存
优点:对于任意一个地址,只需对比一个“标记”,速度最快;
缺点:由于某个主存块只能放到Cache中的固定位置,Cache存储空间利用不充分,命中率低
对于组相联映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行,行诊为64B。
组相联映射,所属分组=主存块号%分组数假设Cache采用2路组相联映射---2块为1组,分四组
分为4组,所属分组=主存块号%分组数=主存块号%2^2,相当于只保留了主存块号的末尾2位来表示所属分组的组号,既然主存块出现在Cache中的同一组,那么说明主存块号末尾2位一定相同,所以标记就没有必要记录这两位了,所以对于这题的标记,只需要取主存块号前20位即可
总结:
CPU访问主存地址:1....1101001110
① 根据主存块号的后2位确定所属分组号
② 若主存块号的前20位与分组内的某个标记匹配且有效位=1,则Cache命中,在Cache中访问块内地址为 001110 的单元。
③若未命中或有效位=0,则正常访问主存
优点:另外两种方式的折中,综合效果较好
注:n路组相联映射----每n个Cache行为一组
4.替换算法
Cache很小,主存很大,而每次被访问的主存块,一定会被立即调入Cache,如果Cache满了怎么办?
(1)对于全相联映射
对于这种方式,每一个主存块,可能被放到Cache中的任何块中,所以只有Cache完全满了才需要替换需要在全局选择替换哪一块
(2)对于直接映射
对于这种方式,某一主存块会被放到Cache中的指定位置,所以如果对应位置非空,则毫无选择地直接替换
(3)对于组相联映射
对于这一方式,某一主存块会被放到固定分组中的任意位置,分组内满了才需要替换,需要在分组内选择替换哪一块
所以替换算法只会被应用到全相联映射与组相联映射中,对于直接映射,无需考虑替换算法,这里以全相联映射为例,讲解以下替换算法:
(1)随机算法(RAND)
随机算法(RAND,Random)----若Cache已满,则随机选择一块替换
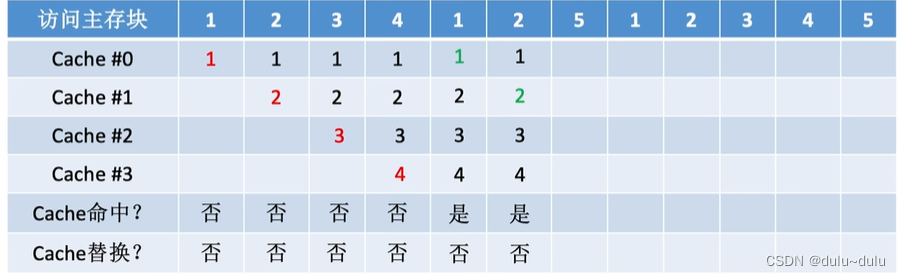
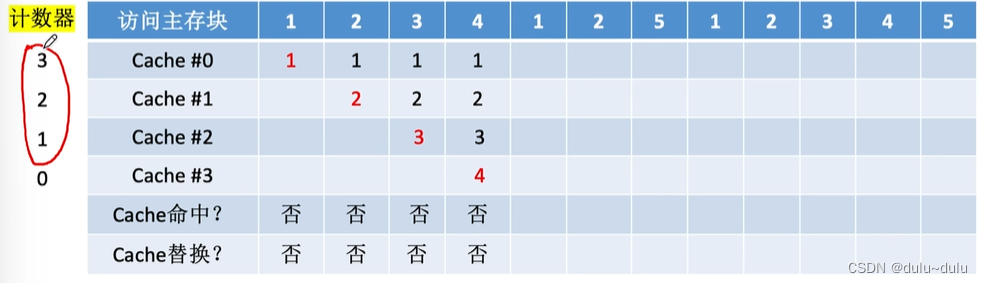
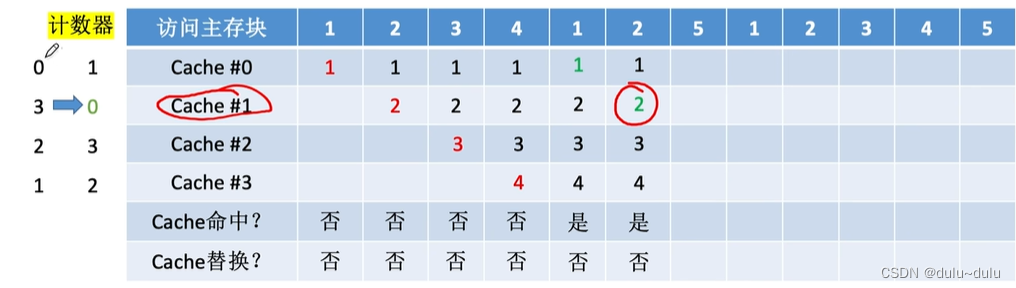
设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5,1, 2,3,4,5}
如图所示,每访问一个主存块,都需要将其从主存调入Cache,由于前4次访问,Cache都未被装满,所以不需要进行Cache替换

由于1,2号主存块已经在Cache中,所以Cache命中
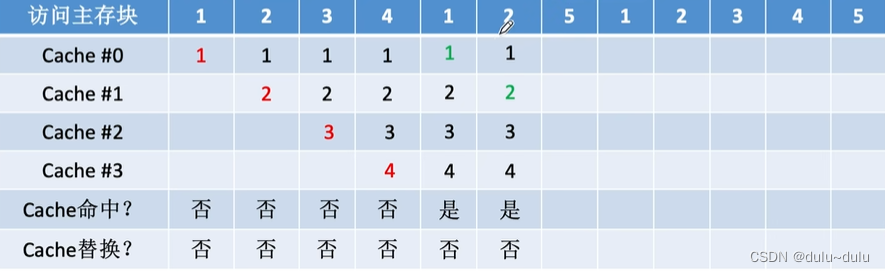
现在访问5号主存块,就需要立即将5号主存块调入Cache,根据随机算法的规则,则随机选择一个Cache块替换,其他同理:
随机算法----实现简单,但完全没考虑局部性原理,命中率低,实际效果很不稳定
(2)先进先出算法(FIFO)
先进先出算法(FIFO,First In First Out)--若Cache已满,则替换最先被调入Cache 的块
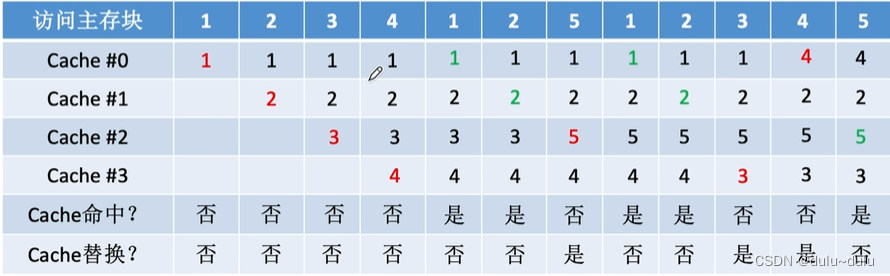
设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5, 1, 2, 3, 4, 5}
前面与随机算法同理:
接下来访问5号主存块,由于5号主存块没有在Cache中,所以5号主存块会被调入Cache,根据先进先出的规则,由于最先被调入的是1号主存块,所以1号主存块先被淘汰,将5号主存块放入1号主存块原来放的Cache中:
现在在Cache中,最先调入Cache的是2号主存块,所以淘汰2号主存块,将1号主存块放入到2号主存块原来放的Cache中,其他以此类推:
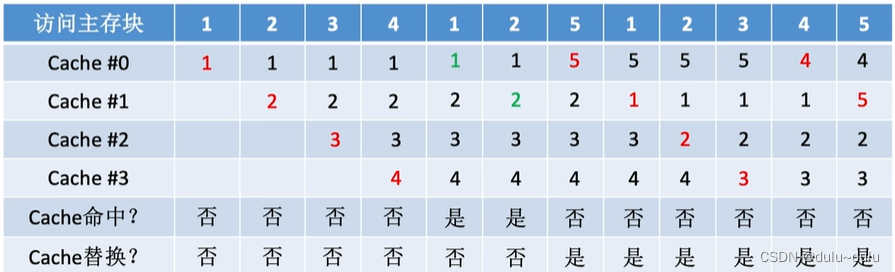
先进先出算法----实现简单,最开始按#0#1#2#3(Cache行号递增的方式)放入Cache,之后轮流替换#0#1#2#3
FIFO依然没考虑局部性原理,最先被调入Cache的块也有可能是被频繁访问的,同时先进先出算法会出现抖动现象:频繁的换入换出现象(刚被替换的块很快又被调入)
(3)近期最少使用(LRU)
近期最少使用算法(LRU,Least Recently Used)----为每一个Cache块设置一个"计数器",用于记录每个Cache块已经有多久没被访问了。当Cache满后替换“计数器”最大的
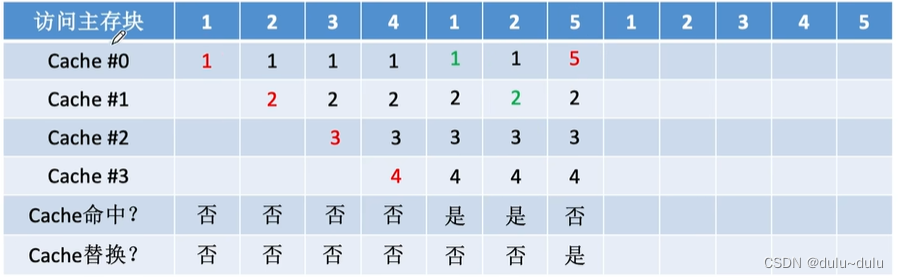
如下图所示,接下来需要将5号内存块调入Cache,那么从5这个位置往前看,依次为2,1,4,3,所以最久未被访问的是3号内存块,替换3号内存块,调入5号内存块

所以若需要将某一内存块调入Cache,就从这一内存块往前看,替换最久未被访问的内存块
若使用近期最少使用算法,每个Cache行不仅需要记录标记和有效位,还必须记录"计数器"
①命中时,所命中的行的计数器清零,比其低的计数器加1,其余不变;
②未命中且还有空闲行时,新装入的行的计数器置0,其余非空闲行全加1;
③未命中且无空闲行时,计数值最大的行的信息块被淘汰,新装行的块的计数器置0,其余全加1。
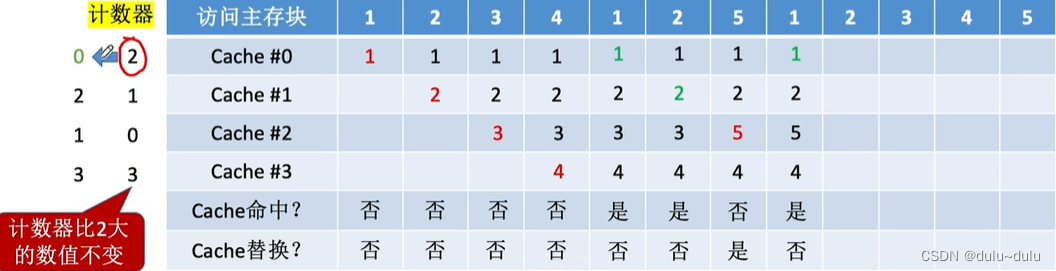
例如,刚开始1号主存块被调入Cache中,没有命中,并且依然有空闲行,所以1号主存块被调入0号Cache中,那么将0号Cache行的计数器置0,因为其他行也空闲,所以不需要加1;
同理,2号主存块调入到1号Cache中,那么将2号Cache的计数器置0,并且将0号Cache加1,依次类推:
接下来访问1号内存块,由于Cache命中,那么会把命中的行计数器清零,比其更低的计数器加1,其余不变
2号内存块同理:
接下来5号内存块会替换"计数值最大"的行,新装入行的块计数器置0,其余全部加1
接下来访问1号内存块,Cache命中,所以把命中的行的计数器清零,比其低的计数器加1,其余不变
在这里我们同样可以把3+1=4,但是这是没有必要的,因为设置计数器是想通过判断值的大小,选择要替换的内存块,要替换"计数器"最大的,所以就算不加+1,3也是最大的
注:由于Cache填满前计数的起点是不同步的,接下来填满后,若要替换,也是一次替换一个内存块,所以一定不会有相同的计数
计数器比2大的数值不变的好处有以下两个:
①当只有4个Cache行时,计数器的值只可能出现0,1,2,3,Cache块的总数=2^n,则计数器只需n位。且Cache装满后所有计数器的值一定不重复
②若以下图中,CPU一直访问内存块1,如果不设置这一机制,则计数器一直+1,可能导致计数器溢出
其他同理,最终得到:
LRU算法----基于"局部性原理",近期被访问过的主存块,在不久的将来也很有可能被再次访问,因此淘汰最久没被访问过的块是合理的。LRU算法的实际运行效果优秀,Cache命中率高。
但若被频繁访问的主存块数量>Cache行的数量,则有可能发生“抖动”,如:{1,2,3,4,5,1,2,3,4,5,1,2...}
(4)最近不经常使用(LFU)
最不经常使用算法(LFU,Least Frequently Used )----为每一个Cache块设置一个“计数器”,用于记
录每个Cache块被访问过几次。当Cache满后替换“计数器”最小的
① 新调入的块计数器=0,之后每被访问一次计数器+1。需要替换时,选择计数器最小的一行
② 接下来访问5号主存块,需要替换"计数器"最小的内存块,若有多个计数器最小的行,可按行号递增或FIFO策略进行选择,例如可以优先淘汰行号较小的块或淘汰先进的内存块,所以这里替换2号Cache行中的内存块

这里按照优先淘汰行号较小的块的规则,最终得到:
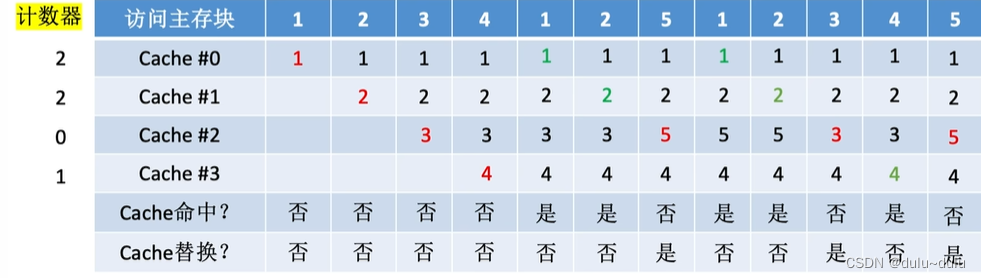
采用这种算法的话,计数器的取值范围:0~很大的值,那么每个Cache行所对应的计数器,就需要使用较长的位数表示
同时,对于LFU算法---曾经被经常访问的主存块在未来不一定会用到(例如某段时间频繁使用微信视频聊天相关的块,此时相关计数器会增加到很大,若之后不再需要视频聊天,但相关Cache块的计数器已经很大了,所以相关内存块在Cache中的数据副本在短时间内不会被淘汰),并没有很好地遵循局部性原理(最不经常使用算法可能会记录下全局的访问频率),因此实际运行效果不如LRU
5.Cache写策略
CPU修改了Cache中的数据副本,如何确保主存中数据母本的一致性?
(1)写命中
•写回法
写回法(write-back)----当CPU对Cache写命中时,只修改Cache的内容,而不立即写入主存,只有当此块被换出(淘汰)时才写回主存
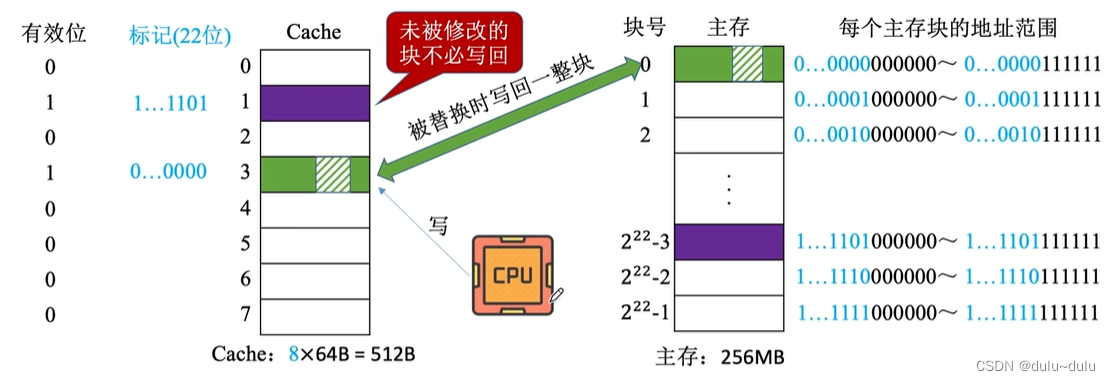
为了让硬件能够区分哪个Cache块被修改过,哪个没有被修改过,需要为每个Cache行增加一个脏位,当一个Cache行的数据块被修改,需要将这一Cache行对应的脏位置1 ,这样当我们淘汰某一Cache行时,就可以判断这一Cache行是否需要被写入主存,而写回主存的什么位置,则可以通过标记判断
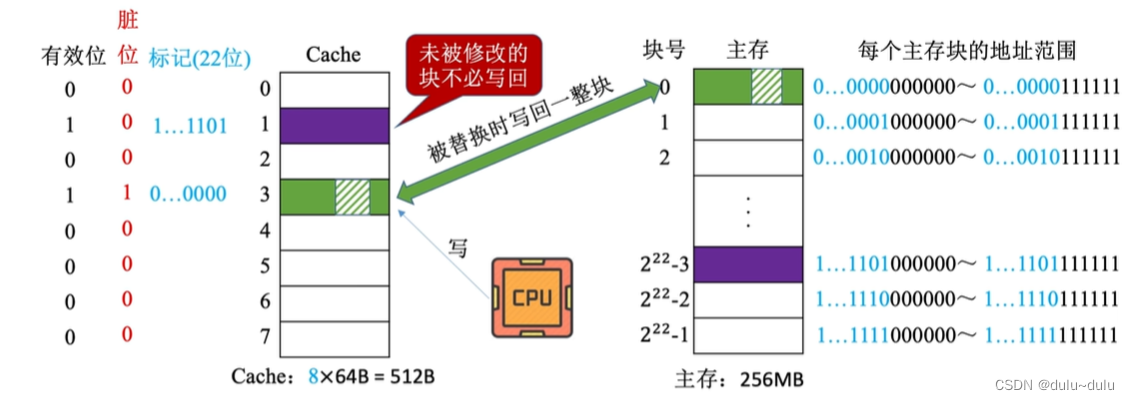
这种方式减少了访存次数,但存在数据不一致的隐患。
•全写法
全写法(写直通法,write-through)----当CPU对Cache写命中时,必须把数据同时写入Cache和主存,一般使用写缓冲(write buffer)
当Cache行中的数据被淘汰时,也不需要写回主存中,因为数据随时都是保持一致的
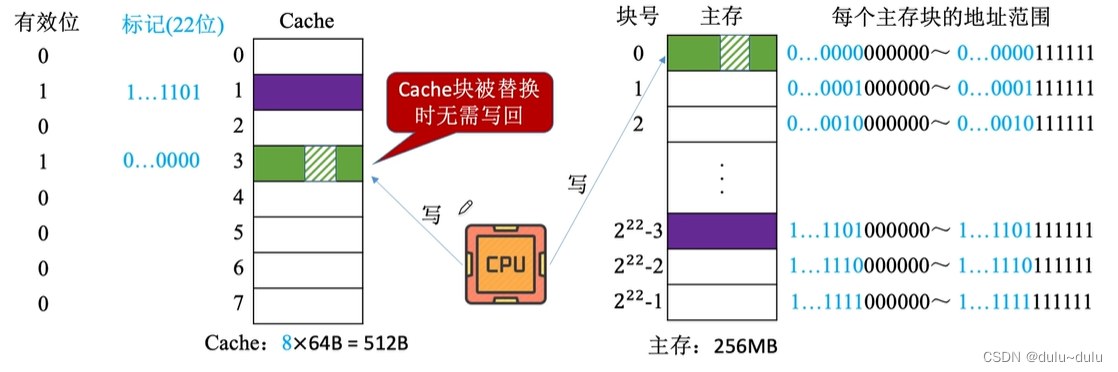
采用这种方法,CPU每次进行写操作时,除了访问Cache,也需要访问主存,访存次数增加,速度变慢,通常增加写缓存(write buffer),写缓存是用SRAM制造的,对写缓冲的读写会比较快
当CPU对某一地址的数据进行写操作,并且这一地址命中时,CPU首先会向Cache中写入这些数据,另外CPU也会向写缓冲中写入相应的数据,由于写缓存是由SRAM实现的,所以写入写缓冲要比写入主存更快

接下来CPU就可以做其他事了,在这期间,写缓冲会在专门的控制电路控制下逐一写回
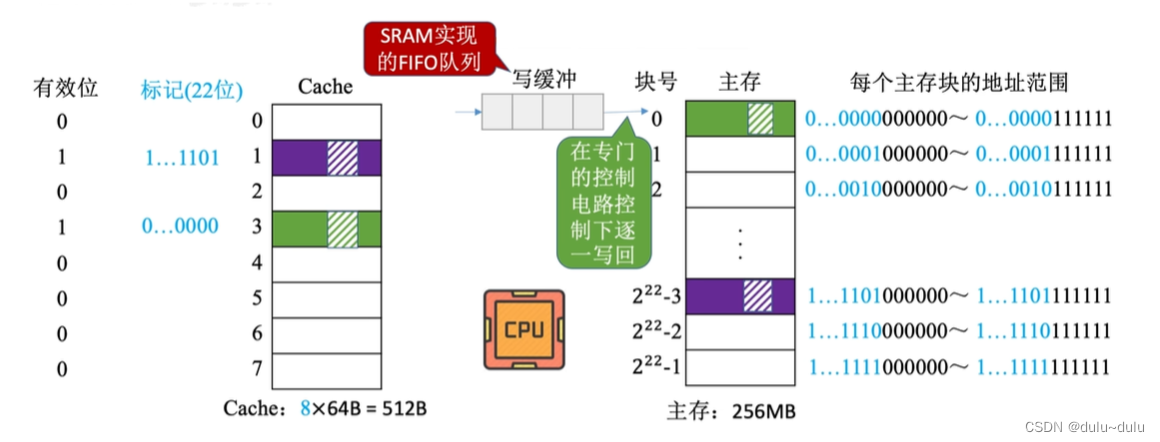
使用写缓冲,CPU写的速度很快,若操作不频繁,则效果很好。若写操作很频繁,可能会因为写缓冲饱和而发生阻塞
(2)写不命中
•写分配法
写分配法(write-allocate)---当CPU对Cache写不命中时,把主存中的块调入Cache,在Cache中修改。(也就是主存的数据不动,CPU只是修改了Cache中的副本) 通常搭配写回法(也就是Cache块被淘汰后,才把一整块的数据同步回主存)使用。
•非写分配法
非写分配法(not-write-allocate)---当CPU对Cache写不命中时只写入主存,不调入Cache。
搭配全写法(当CPU对Cache写命中时,必须把数据同时写入Cache和主存)使用。
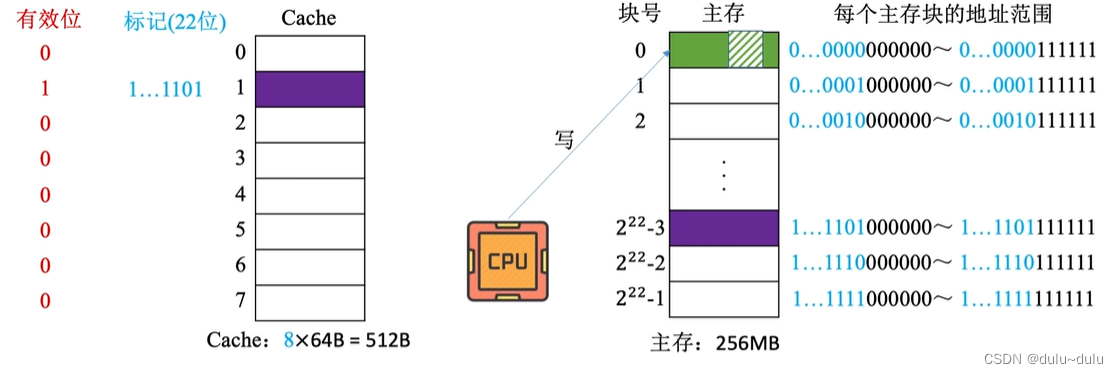
用这种方法,只有CPU进行"读"操作未命中时,才会把相应主存块调入Cache,而如果是"写"操作未命中时,只写入主存,不调入Cache
补充:
现在计算机常采用多级Cache
离CPU越近的速度越快,容量越小,离CPU越远的速度越慢,容量越大
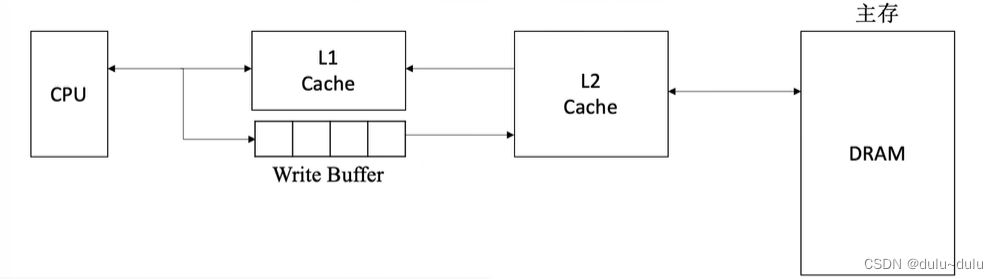
对于上图,L2 Cache保存的是一小部分主存数据的副本,而对于更高级的Cache,则保存的是更低一级Cache的一部分数据的副本,所以Cache之间也存在数据一致性的问题
① 各级Cache之间常采用"全写法+非写分配法"
② Cache--主存之间常采用"写回法+写分配法"



















)


)
)
 「精选篇」)










