简介:
KMP算法是一种改进的字符串匹配算法,其中,KMP算法的运用核心是利用匹配失败后的信息,最大进度的减少模式串与目标串的匹配次数以达到快速匹配的效果。算法与暴力求解的改进在于每当一趟匹配过程中出现的字符比较不相等时,指向目标串的指针不在回到"原点",而是利用已经得到的”部分匹配“的结果将模式串向右移动最大且和目标串已匹配的距离后进行比较,总的来说就是目标串不回退,模式串回退,直到结束为止。
KMP实现如图:
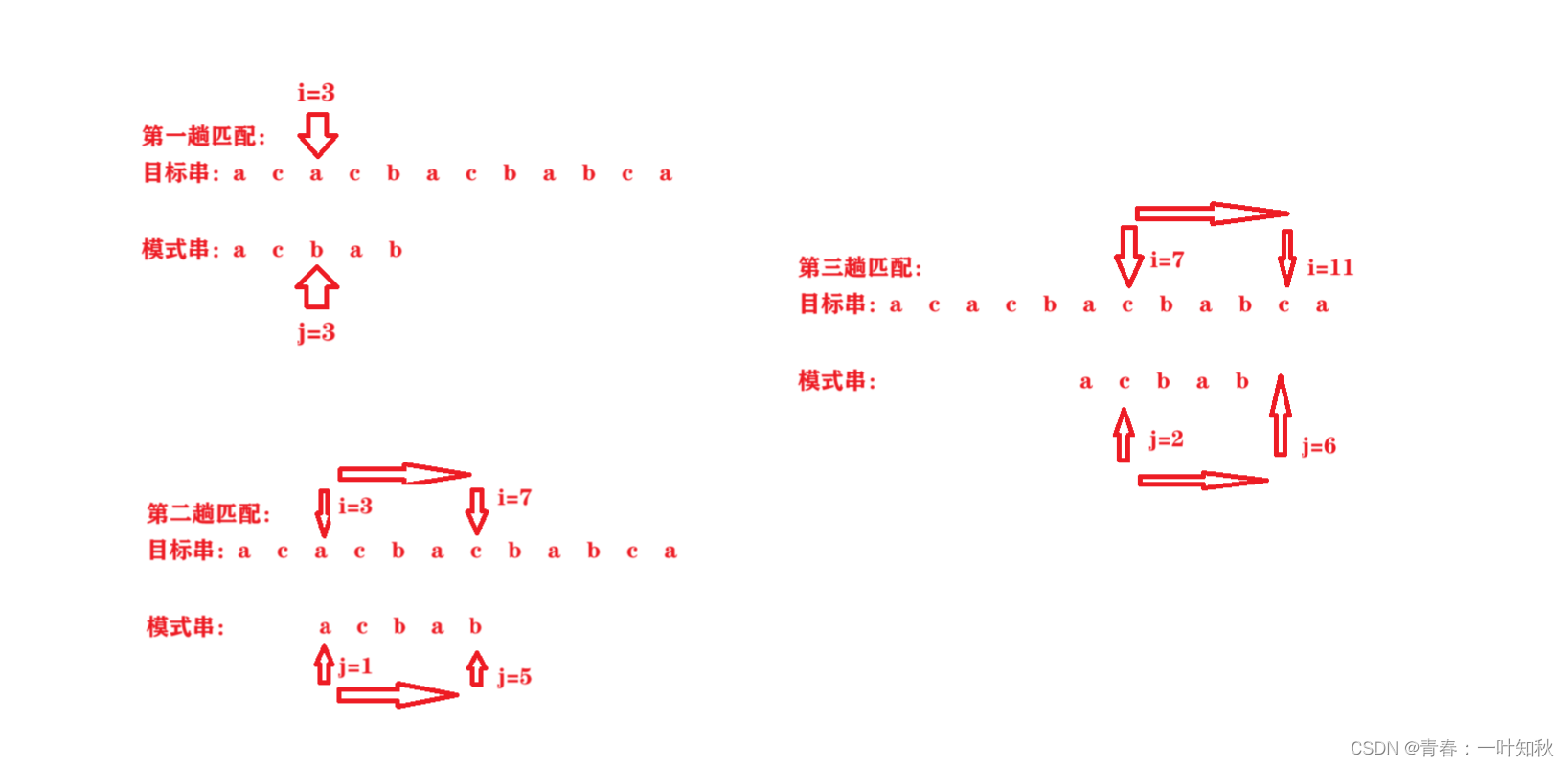
在图中,第一次比较不成功时,i= 3,j = 3,此时,i指针不变,需要将模式串向右移动两个字符的位置,继续进行i = 3,j = 1的下一趟比较;第二趟匹配中,前四个字符比较成功,但i = 7, j = 5时比较失败,此时将模式串向右移动3个字符的位置,继续进行i = 7,j = 2的下一趟比较,直至比较成功。
注意,在整套算法体系中,指向目标串的指针i不会退,因此,一旦模式串在某个位置匹配失败后就要回退到某个位置与目标串继续进行匹配。
模式匹配:
然而,在此,我们可发现,KMP算法中难点就在于模式串在匹配失败后要回退的位置。
目标串的每个元素都要进行模式匹配,因此,当模式串的每个元素都有一个回退某个具体位置的指标,我们用next整型数组进行存储,即next[j] = k(j模式串的具体位置,k 为回退到模式串的具体位置)。
其中,k的值是这样规定的:
1,规则:找到匹配成功部分的两个相等的真子串(注意:不包含本身,因为本身还要进行匹配),一个以下标0开始,另一个以j - 1下标结尾,即模式串的头部和尾部(原因可思考一下)。
2,不管什么数据next[0] = -1;next[1] = 0;在这里,我们以下标来开始,而说到的第几个是从1开始。
下面我们运用以上原理来求模式串的next数组:

以上的定位数组next的定位一定要根据模式串与目标串前后匹配成功的最大次数来定,而具体的匹配是根据模式串的前面和目标串的某个可以与之匹配的最大次数。
到这里,我们手动求解定位数组next问题不大,那么,接下来要怎么用代码来求解呢?首先,我们先来观察已知条件,在求解next[i + 1]中,我们已知next[i] = k;如果我们能够通过next[i]的值,再根据数学转换得到next[i + 1]的值,那么就能够实现整个数组的内容。
首先,已知数组next[i] = k成立,具体的实现next数组我用图形的形式跟大家来演示:

接下来我用C代码的形式来演示一遍定位数组的求解:
//next代表定位数组,a代表模式串,lena代表模式串的长度
void Next(int* next, char* a, int lena)
{next[0] = -1;next[1] = 0;int j = 2, k = 0;while (j < lena) {if (k == -1 || a[k] == a[j - 1]) {next[j] = k + 1;j++;k++;}else{k = next[k];}}
}其中,定位数组算法的时间复杂度效率为O(lena)
具体运用代码如下:
int KMP(char* str, int strlen, char* a, int alen, int* next)
{assert(strlen || alen);int i = 0, j = 0;while (i < strlen && j < alen) {//匹配成功,进行下一步if (j == -1 || str[i] == a[j]) {i++;j++;}//当不满足匹配时,进行回退,直到匹配成功为止else {j = next[j];}}//模式匹配成功if (j == alen) {return i - j + 1;}//模式匹配失败else {return -1;}
}补:部分书籍KMP高效匹配可能有些不同,但基本思路都相同,此算法的效率很高,时间复杂度为O(alen + strlen).
















—Matlab+Yalmip两阶段鲁棒优化通用编程指南(下))


