1、B站视频链接：B14 BFS 八数码难题_哔哩哔哩_bilibili

题目链接：八数码难题 - 洛谷

#include <bits/stdc++.h>
using namespace std;
char c;
string str;
unordered_map<string,int> d;//记录步数
queue<string> q;
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};int bfs(string str){q.push(str);string end="123804765";while(q.size()){auto s=q.front();q.pop();if(s==end)return d[s];int k=s.find('0');int x=k/3,y=k%3;//一维变二维，映射到九宫格对应坐标上for(int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if(a<0||a>=3||b<0||b>=3)continue;int dis=d[s];//记录步数swap(s[k],s[a*3+b]);//交换，乘3加余数if(!d.count(s))d[s]=dis+1,q.push(s);//新布局，步数加一 swap(s[k],s[a*3+b]);//还原继续探照其它的方向 } }
}
int main(){for(int i=0;i<9;i++){cin>>c;str+=c;}cout<<bfs(str);return 0;
} 

2、B站视频链接：B15 BFS 抓住那头牛_哔哩哔哩_bilibili

题目链接：[USACO07OPEN] Catch That Cow S - 洛谷 

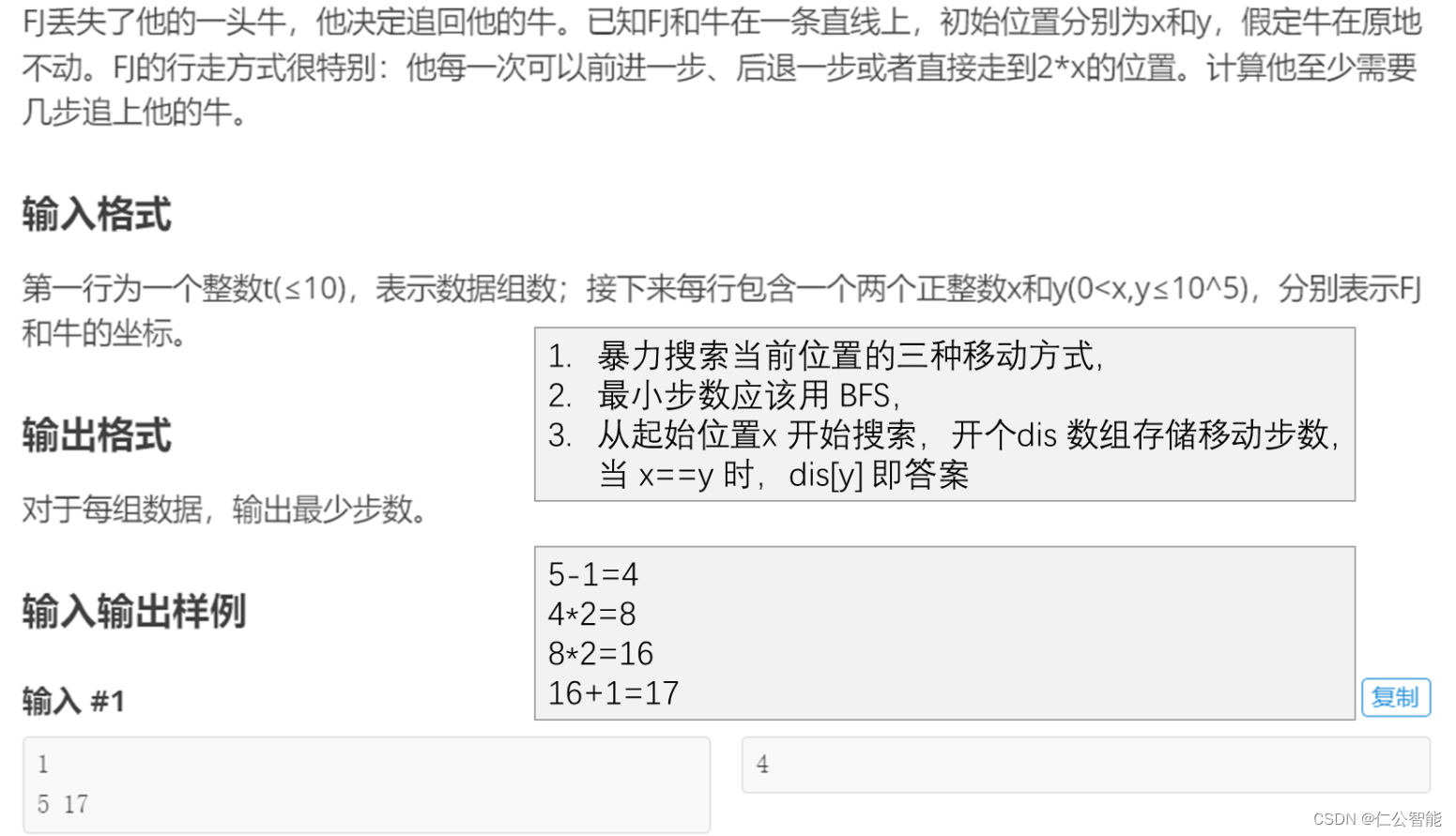
#include <bits/stdc++.h>
using namespace std;const int N=100010;
int x,y,dis[N];//记录步数 void bfs(){memset(dis,-1,sizeof dis);//初始化步数dis[x]=0;queue<int> q;q.push(x);//人的位置入队while(q.size()){int x=q.front();q.pop();if(x+1<N&&dis[x+1]==-1){//前进一步，剪枝判重 dis[x+1]=dis[x]+1;//步数加一q.push(x+1);//更新人的位置入队 }if(x-1>0&&dis[x-1]==-1){//后退一步 dis[x-1]=dis[x]+1;q.push(x-1);}if(x*2<N&&dis[2*x]==-1){//走到2*x dis[2*x]=dis[x]+1;q.push(2*x);}if(x==y){//抓住了牛 printf("%d\n",dis[y]);//抓住牛需要的步数 return;}} 
}
int main(){int t;cin>>t;while(t--){cin>>x>>y,bfs();}return 0;
}

3、B站视频链接：B16 BFS 魔板_哔哩哔哩_bilibili

题目链接：[USACO3.2] 魔板 Magic Squares - 洛谷

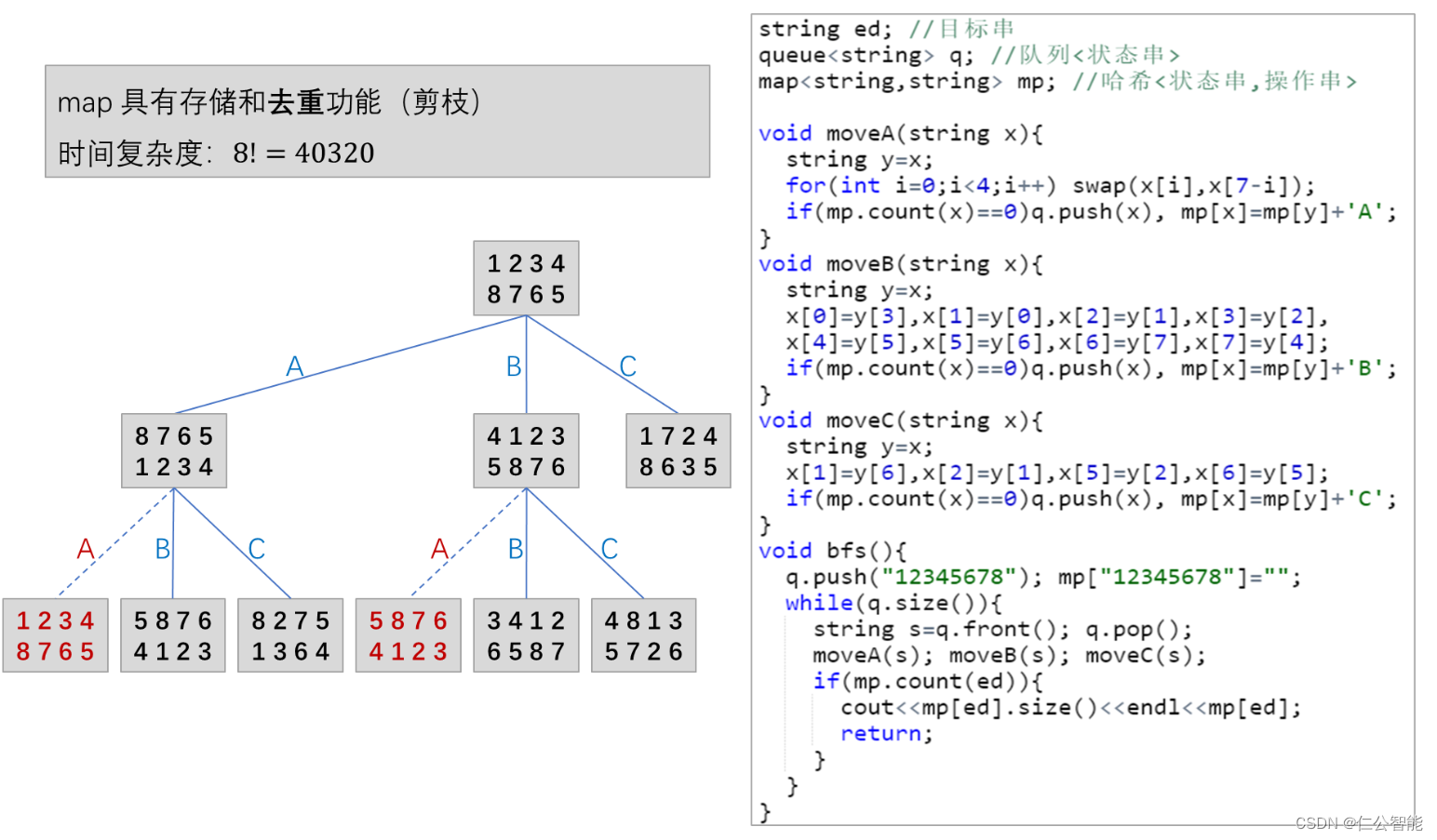
#include <bits/stdc++.h>
using namespace std;
string ed;//目标串（别用end取名，会报错）
queue<string> q;//队列<状态串>
map<string,string> mp;//哈希<状态串，操作串>void moveA(string x){string y=x;for(int i=0;i<4;i++)swap(x[i],x[7-i]);if(mp.count(x)==0)q.push(x),mp[x]=mp[y]+'A';
}
void moveB(string x){string y=x;x[0]=y[3],x[1]=y[0],x[2]=y[1],x[3]=y[2],//暴力一一对应 x[4]=y[5],x[5]=y[6],x[6]=y[7],x[7]=y[4];if(mp.count(x)==0)q.push(x),mp[x]=mp[y]+'B';
}
void moveC(string x){string y=x;x[1]=y[6],x[2]=y[1],x[5]=y[2],x[6]=y[5];if(mp.count(x)==0)q.push(x), mp[x]=mp[y]+'C';
}
void bfs(){q.push("12345678");mp["12345678"]="";//无操作while(q.size()){string s=q.front();q.pop();moveA(s);moveB(s);moveC(s);if(mp.count(ed)){cout<<mp[ed].size()<<endl<<mp[ed];return ;}}
}
int main(){char c;for(int i=0;i<8;i++){cin>>c,ed+=c;}bfs();return 0;
}