数学建模：BP神经网络（含python实现）

原理

BP 神经网络，也称为多层感知机（Multilayer Perceptron，MLP），是一种常见的神经网络模型，用于解决各种机器学习问题，包括分类和回归。BP 代表“反向传播”（Backpropagation），这是该模型训练的关键算法。
BP 神经网络由多个神经元组成，通常分为输入层、隐藏层和输出层。每个神经元都与前一层的每个神经元相连，并且具有权重，用于调整信号的传递和计算。BP 神经网络的原理基于前向传播和反向传播两个关键步骤。
前向传播是在前向传播过程中，输入信号从输入层传递到隐藏层和输出层，每个神经元将其输入与权重相乘并应用激活函数来产生输出。这个过程一直持续到达输出层，生成网络的预测结果。输入层到隐藏层公式: $z_j=\sum_{i=1}^{n}w_{ji}^{(1)}x_i$ $\alpha_j=f(z_j)$ 输入层到隐藏层公式： $z_k=\sum_{j=1}^{m}w_{ki}^{(2)}\alpha_j$ $\alpha_k=f(z_k)$ 其中， $z_j$ 和 $z_k$ 分别表示隐藏层和输出层神经元的加权输入， $\alpha_j$ 和 $\alpha_k$ 表示它们的激活输出，𝑤是权重，𝑥是自变量，𝑓是激活函数。
反向传播是在反向传播过程中，网络的输出与实际目标进行比较，以计算误差。然后，误差通过网络反向传播，根据链式规则，将误差分配给每个神经元，并根据误差调整权重，以减小误差。这个过程重复进行多次，直到误差收敛到满意的水平或达到预定的训练轮次。其公式如下： $\Delta w_{kj}^{(2)}=-\eta \frac{\partial E}{\partial w_{kj}^{(2)}}$ $\Delta w_{ji}^{(1)}=-\eta \frac{\partial E}{\partial w_{ji}^{(1)}}$ 其中，其中，𝜂是学习率，∂𝐸，∂𝑤表示误差关于权重的偏导数。误差计算中通常使用均方误差（Mean Squared Error，MSE）作为误差函数： $E=\frac12\sum_{k=1}^p(t_k-\alpha_k)^2$ 其中， $t_k$ 是目标输入， $\alpha_k$ 是网络的实际输出。
BP神经网络结构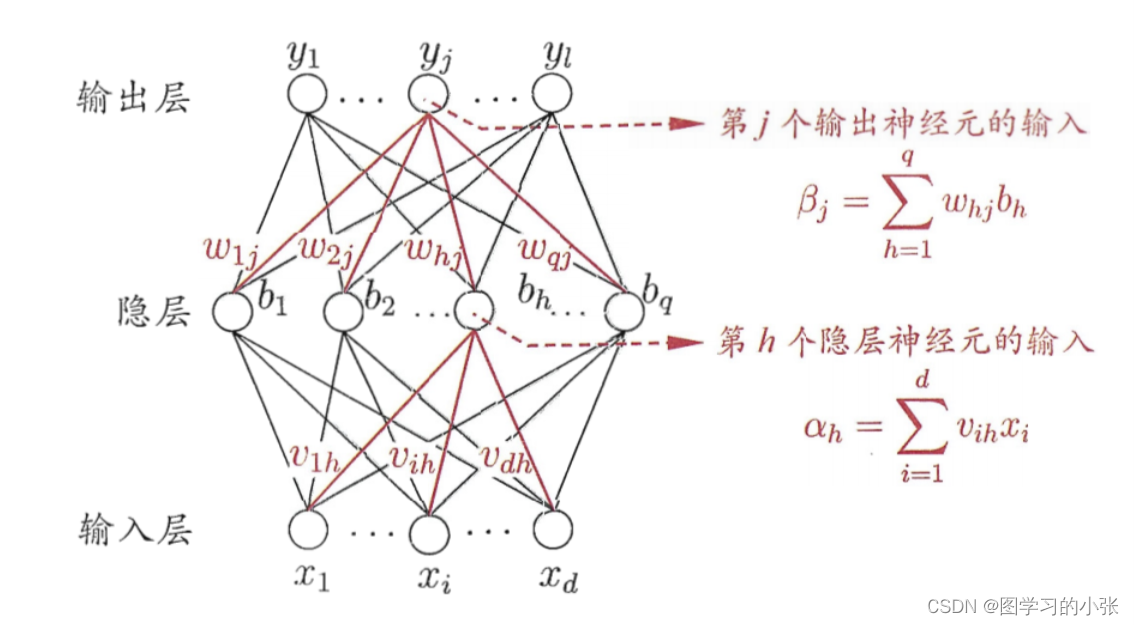：在这里插入图片描述

代码

多层感知机实际上就是多层全连接网络构成的网络，一个示例代码：

import tensorflow as tf
from tensorflow import keras# 定义模型
model = keras.Sequential([keras.layers.Dense(64, activation='relu', input_shape=(X.shape[1],)),keras.layers.Dense(32, activation='sigmoid'),keras.layers.Dense(1, activation='sigmoid')
])
# model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# model.fit(X_train, Y_train, epochs=100, batch_size=32, validation_split=0.05)
# odel = keras.Sequential([
#     keras.layers.Dense(128, activation='relu', input_shape=(X.shape[1],)),
#     keras.layers.Dense(64, activation='sigmoid'),
#     keras.layers.Dense(32, activation='relu'),
#     keras.layers.Dense(16, activation='sigmoid'),
#     keras.layers.Dense(8, activation='relu'),
#     keras.layers.Dense(1, activation='sigmoid')
# ])model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# 模型训练
history=model.fit(X_train, Y_train, epochs=60, batch_size=32, validation_split=0.5)

在这里插入图片描述

# 模型评估
test_loss, test_accuracy = model.evaluate(X_test, Y_test)
print(f'Test accuracy: {test_accuracy}')
# 使用表1的所有行进行水肿概率的预测
# all_predictions = model.predict(X2)
# all_predictions