1. 要求
设计一款信道与信息率失真函数计算系统,要求如下:
- 系统能够通过输入的转移概率矩阵计算对称以及非对称离散无记忆信道的信道容量
- 系统能够通过输入的概率分布以及失真矩阵来计算与信息率失真函数有关的相关参数,例如Dmin,R(Dmin),Dmax,R(Dmax),并且能够给出相应的转移概率矩阵
- 系统通过多个窗体组合,通过总菜单点击不同选项会进入到相应的计算中
- 窗体中应该包括MenuStrip控件,通过控件中的选项进行不同的操作
2. 过程
1.首先进行窗体的设计,根据要求需要一个菜单窗口以及三个计算分别对应的窗口,为了使得系统更加完整再添加一个登录窗口,所以一共需要5个窗口。
先通过登录窗口登录,其中密码在输入时设置为不可见的:

图1 登录窗体
登录后需要进入菜单界面,其设计如下:
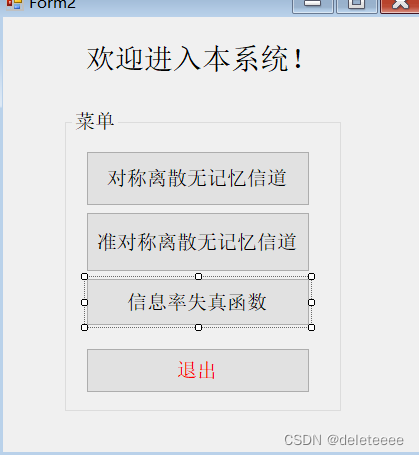
图2 菜单窗体
通过菜单中的按钮进入不同系统,接下来分别是对三个计算系统的设计:
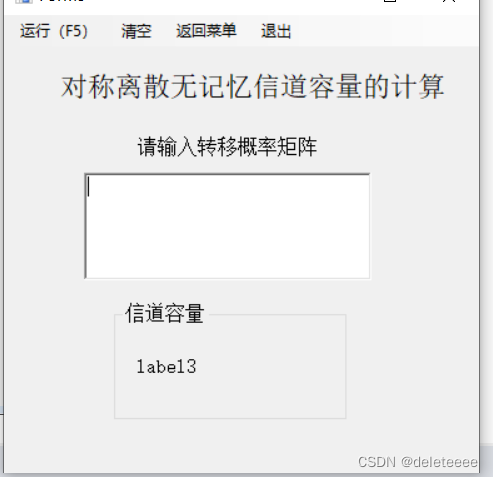
图3 对称离散无记忆信道
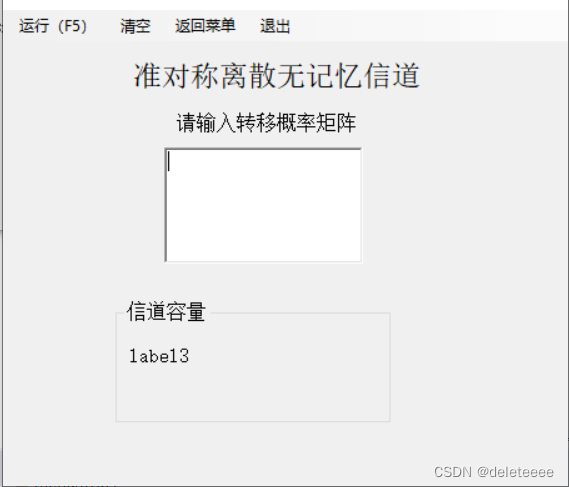
图4 准对称离散无记忆信道
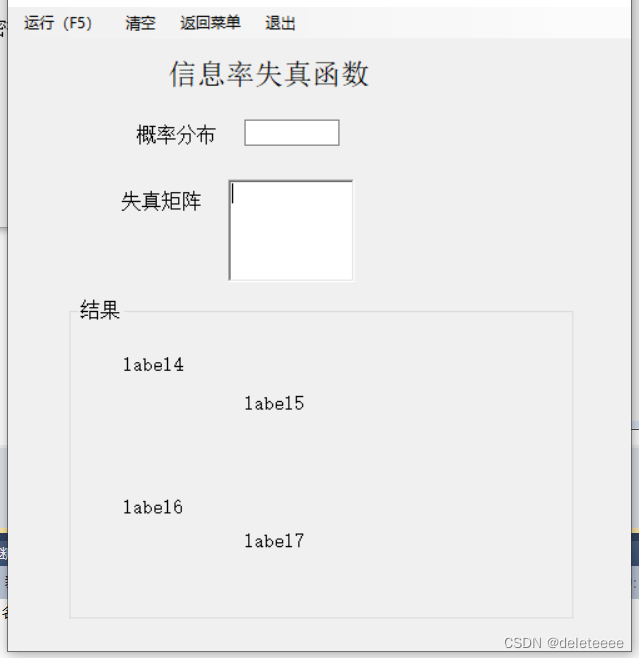
图5 信息率失真函数
以上三个计算窗体中都包含输入与输出,矩阵输入都使用RichTextBox控件,信息率失真函数中多了一个概率分布的输入,使用TextBox控件实现即可。除此之外,它们的MenuStrip控件中都包含有运行、清空、返回菜单、退出共四个选项,其中运行选项可以直接通过快捷键F5来实现。
2.窗体都已经设计完毕,接下来是对相关的按钮或者是选项中的事件进行代码编写。以下只给出准离散信道和信息率失真函数的相关代码及说明。
准离散信道:
private void 运行F5ToolStripMenuItem_Click(object sender, EventArgs e){int a = richTextBox1.Lines.Length; //行数double h = 0; //H(Y|ai)char[] sp = new char[3] { ' ', '\t', '\n' };string[] str1 = new string[100];str1 = richTextBox1.Text.Split(sp);int b = str1.Length / a; //列数string[,] str2 = new string[a, b];double[] tmp = new double[b]; //每一列的和string[,] tp = new string[b, a];double m = 0;//不止一列的子矩阵的行元素求和double z = 0;//只有一列的子矩阵行元素之和乘以列元素之和的对数再求和for (int i = 0; i < a; i++){for (int j = 0; j < b; j++){str2[i, j] = str1[i * b + j];}}for (int i = 0; i < b; i++){tmp[i] = 0;for (int j = 0; j < a; j++){tmp[i] += Convert.ToDouble(str2[j, i]);}if (tmp[i] == tmp[0]){m += Convert.ToDouble(str2[0, i]);}if (tmp[i] != tmp[0]){z += Convert.ToDouble(str2[0, i]) * Math.Log(tmp[i], 2);}}for (int i = 0; i < b; i++){double p = Convert.ToDouble(str2[0, i]);h += p * Math.Log(p, 2);}double C = Math.Log(a, 2) + h - m * Math.Log(tmp[0], 2) - z;//信道容量label3.Text=Convert.ToString(C);}
信息率失真函数:
private void 运行ToolStripMenuItem_Click(object sender, EventArgs e){int a = richTextBox1.Lines.Length;string[] s =textBox1.Text.Split(' ');char[] sp = new char[3] { ' ', '\t', '\n' };string[] str1 = new string[100];str1 = richTextBox1.Text.Split(sp);int b = str1.Length /a;double h = 0;//H(X)double[,] d = new double[a, b];//失真矩阵string[,] pmin = new string[a, b];//Dmin时的转移概率矩阵string[,] pmax = new string[a, b];//Dmax时的转移概率矩阵double[] p=new double[s.Length];//输入概率double[] D=new double[b];//满足R(D)=0中D的值for (int i = 0; i < p.Length; i++){p[i] = Convert.ToDouble(s[i]);h +=-p[i]*Math.Log(p[i],2);}for (int i = 0; i < a; i++){for (int j = 0; j < b; j++){d[i, j] = Convert.ToDouble(str1[i * b + j]);pmax[i, j] = "0";pmin[i, j] = "0";}}for (int i = 0; i < b; i++){D[i] = 0;for (int j = 0; j < a; j++){D[i] += p[j] * d[j, i];}}double min = D[0];//所有满足R(D)=0中D的最小值,即Dmaxfor (int i = 0; i < b; i++)if (D[i] < min)min = D[i];for (int i = 0; i < a; i++){for (int j = 0; j < b; j++){if (d[i, j] == 0)pmin[i, j] = "1";}}for (int i = 0; i < b; i++){if (D[i] == min){for (int j = 0; j < a; j++)pmax[j, i] = "1";break;}}label4.Text = "Dmin=0,R(Dmin)="+Convert.ToString(h)+",转移概率矩阵为";label5.Text="";label6.Text="Dmax="+Convert.ToString(min)+",R(Dmax)=0,转移概率矩阵为";label7.Text="";for (int i = 0; i < a; i++){for (int j = 0; j < b; j++){label5.Text += pmin[i, j]+' ';label7.Text += pmax[i, j]+' ';}label5.Text += '\n';label7.Text += '\n';}}3.以上实验步骤都完成后,再将每一个窗口中的选项一一实现,其中返回菜单的选项直接再将菜单的窗口调用出来即可如下图3.1所示,注意要使用Show()函数才能够对打开的窗口进行操作。最后再每点击按钮打开一个新窗体的时候要自动关闭旧窗体。

至此,实验整体设计结束。
3. 测试
接下来开始对系统进行测试:
登录后进入菜单界面:
图6 菜单界面
点击对称离散无记忆信道进入测试,输入后按下F5运行:

图7 对称离散无记忆信道测试
通过验证,其结果完全正确
此时再点击清空选项发现所有数据都已经清空,可以重新输入。再点击返回菜单选项,系统将会返回菜单。注:以下其它两个计算系统的测试中将不再重复该部分功能的测试。
测试准对称离散无记忆信道:

图8 准对称离散无记忆信道测试1

图9 准对称离散无记忆信道测试2
经过验证,两种测试的结果都是正确的,该部分没有问题。
测试信息率失真函数:
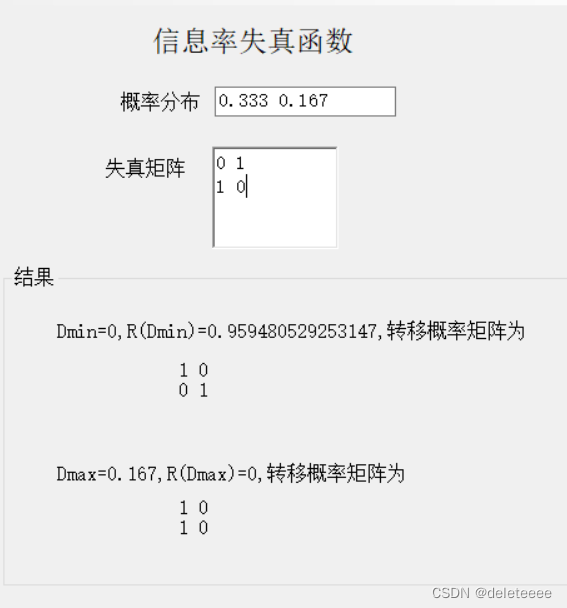
图10 信息率失真函数测试1

图11 信息率失真函数测试2

图12 信息率失真函数测试3
依次对上述测试结果进行验证后得知均为正确结果,但是同时也发现,Dmax时的转移概率矩阵可能并不唯一,本程序只给出其中第一个满足条件的结果。
测试完毕,所有要求均已经实现。
4. 总结
在对称和准对称离散无记忆信道的实验中,我只是给出了它们的信道容量,没有进一步给出它们更多的相关属性,而在信息率失真函数的实验中,我给出的结果是Dmin与Dmax两个状态的相应属性,而没有对R(D)这个函数作进一步分析,例如还可以增加R(D)函数的曲线图,然后通过改变参数来进一步增加对比实验进行深入分析。信道容量和信息率失真函数都可以为通信所服务,引入信道容量能够为信道编码服务,提高通信的可靠性,而引入信息率失真函数可以为信源的压缩编码服务,提高通信的有效性。





)
-k8s存储对象Persistent Volume Claim)




)







