前言：如题，我在已知一个平面L和物体A，我希望得到镜像后的物体B的位置和旋转。

效果：

推导：

首先我们需要知道物体的对称坐标A'，我们现在能已知A坐标以及平面L的法线，如果我们能得到B的坐标，我们可以根据中点公式C=1/2(a+b)，反推得到对称点A'，所以我们现在需要求出B点的坐标。

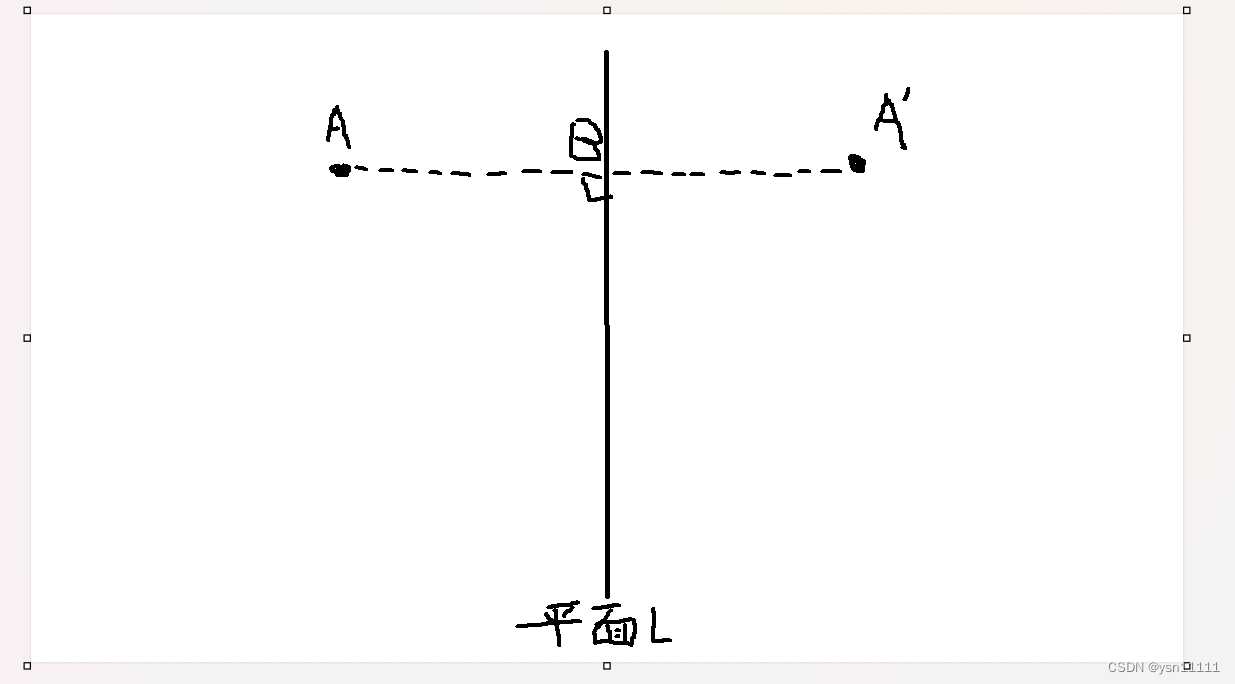
常规数学上的思路：根据平面L=ax+by+cz+d(a,b,c,d都是已知)，法向量是(a,b,c)，并且已知A点的坐标，我们用点向式去表示直线AB，我们能得知方向向量就是平面L的法向量，再已知过点A，我们就能知道直线AB，然后联立求直线和平面L的交点就能知道B点。

但在Unity里面，我们得不到平面的公式，只能得知平面的法向量以及平面上的某一点。所以我们可以通过点乘去得到想要的坐标。比如下面S假设是L的单位法向量，C是平面上的任意一点，我们可以借助Vector3.Dot求出AB的长度，再乘以单位法向量知道AB向量，最终得到B点的坐标。

求出对称后的坐标，还需要求对称后的旋转，我们只要确定两个轴的朝向就能确定旋转。数学上的常规思路比较复杂，有兴趣可以查查，这里就不在赘述。在Unity里面我们知道物体的局部坐标系，比如A的Z轴，如果求出反射向量Z' ，那么物体A’的Z轴指向的其实就是反射向量Z'，这句话很关键。然后我们同理求出A’的y轴的指向就能最终确定A'的旋转。

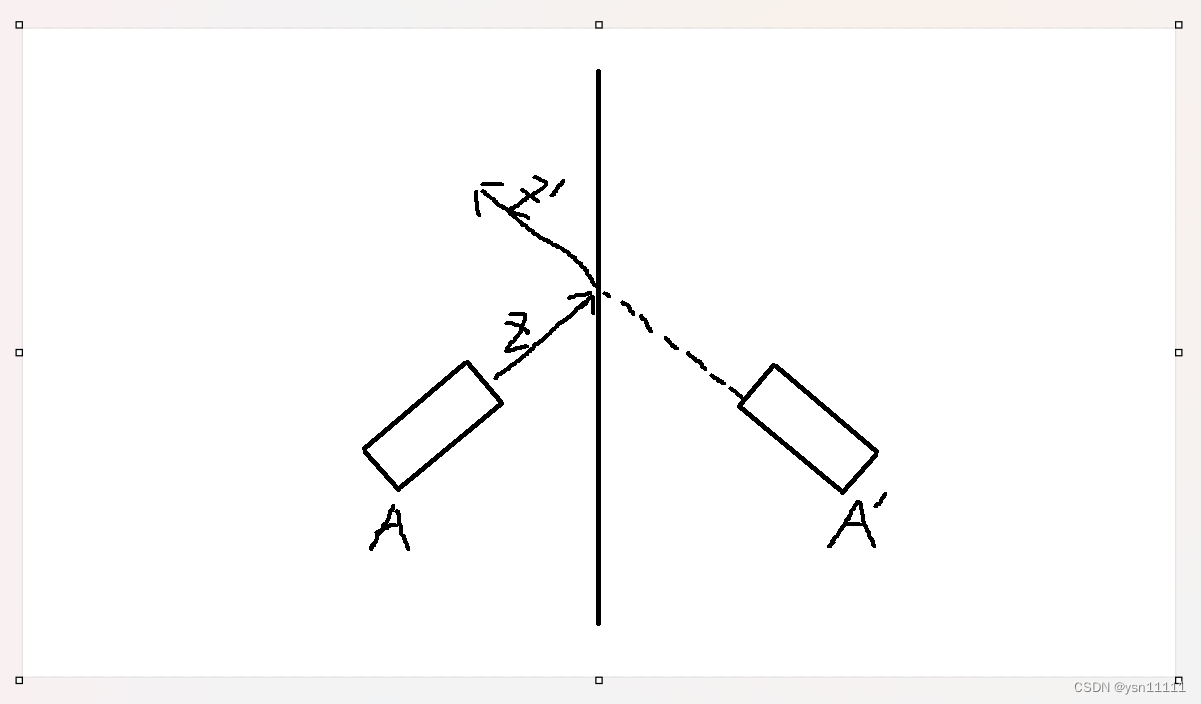
代码：

public class Test : MonoBehaviour
{//目标物public GameObject target1;//镜像物体public GameObject target2;//平面public GameObject panel;private void Update(){//求中心点Vector3 centerPos =ProjectPointOntoPlane(target1.transform.position, panel.transform.position, panel.transform.up);//求镜像坐标点target2.transform.position = 2 * centerPos - target1.transform.position;//求镜像旋转target2.transform.rotation = ProjectReflectRt(target1.transform, panel.transform.up);}// 计算点在平面上的投影坐标(目标点，平面上一点，平面的单位法向量)private Vector3 ProjectPointOntoPlane(Vector3 point, Vector3 planePoint, Vector3 planeNormal){// 计算投影向量Vector3 projectionVector = point - planePoint;float distance = Vector3.Dot(projectionVector, planeNormal);return point - distance * planeNormal;}//计算对称后的旋转private Quaternion ProjectReflectRt(Transform target,Vector3 planeNormal){Vector3 up = target.transform.up;Vector3 forward = target.transform.forward;Vector3 symmetricUp = Vector3.Reflect(up, planeNormal).normalized;Vector3 symmetricForward = Vector3.Reflect(forward, planeNormal).normalized;return Quaternion.LookRotation(symmetricForward, symmetricUp);}
}