文章目录
- ICP匹配方法(Point to Point)
- PL-ICP匹配方法(Point to Line)
- 基于优化的匹配方法(Optimization-based Method)
- 优化方法的求解
- 地图双线性插值
- 拉格朗日插值法——一维线性插值
- 相关方法(Correlation-based Method)
- 帧间匹配似然场
- 算法流程
- 位姿搜索
- 分枝定界算法
- 引用
在激光SLAM中,前端配准(Frontend Registration)是实现定位和地图构建的关键步骤之一。它的作用是将当前帧的激光扫描数据与先前帧(或参考帧)的激光扫描数据进行配准,以获取它们之间的相对位姿变换。
通过前端配准,激光SLAM系统可以实现对机器人在环境中的位置和姿态的估计,以及构建准确的地图。前端配准的准确性对于后续的位姿图优化、环路闭合和地图更新等步骤具有重要影响,因此它是激光SLAM中的关键组成部分。
- 前端配准在视觉内叫做Tracking或者帧间匹配,对激光SLAM是有非常大的影响的
- 帧间匹配不一定说的是前后两帧进行匹配,也可以是任意帧之间进行匹配
- 是一个Map—>Scan的过程,一个Scan和一个Map去匹配的过程
ICP匹配方法(Point to Point)
基本目的: 两个点云进行配准
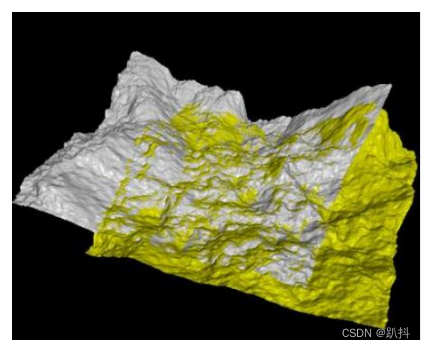
数学描述:

设xi和pi是匹配的,即两个点云中的点打向的是物理空间中的同一个点。因此,我们需要找到R和t,使得两个匹配点的距离最小:
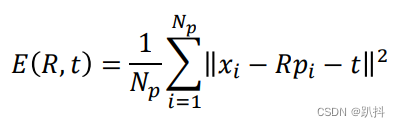
已知对应点的求解方法(解析解):
ux表示点云集合X的几何中心(基准位姿/平均位姿),up表示点云集合P的几何中心(基准位姿/平均位姿),随后把每个点云都移动到平均位姿来。
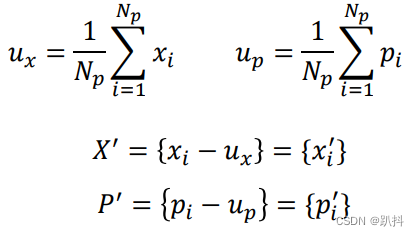
对W进行SVD分解:
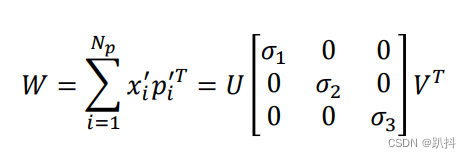
则ICP的解为:
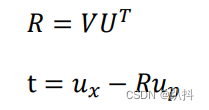
效果如下:
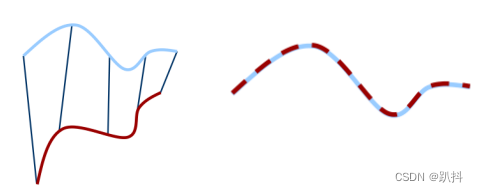
已知对应点的求解方法——证明:


未知对应点的求解方法:

PL-ICP匹配方法(Point to Line)
PL-ICP 实际就是point-to-line ICP,是点到线的ICP方法。相比于传统的ICP方法,即点到点的匹配方法,PL-ICP的流程其实和ICP的流程是一样的,不同的地方在于ICP是找最近邻的一点,以点与点之间的距离作为误差,而PL-ICP是找到最近邻的两点,两点连线,是以点到线的距离作为误差。
ICP的匹配算法的缺点:
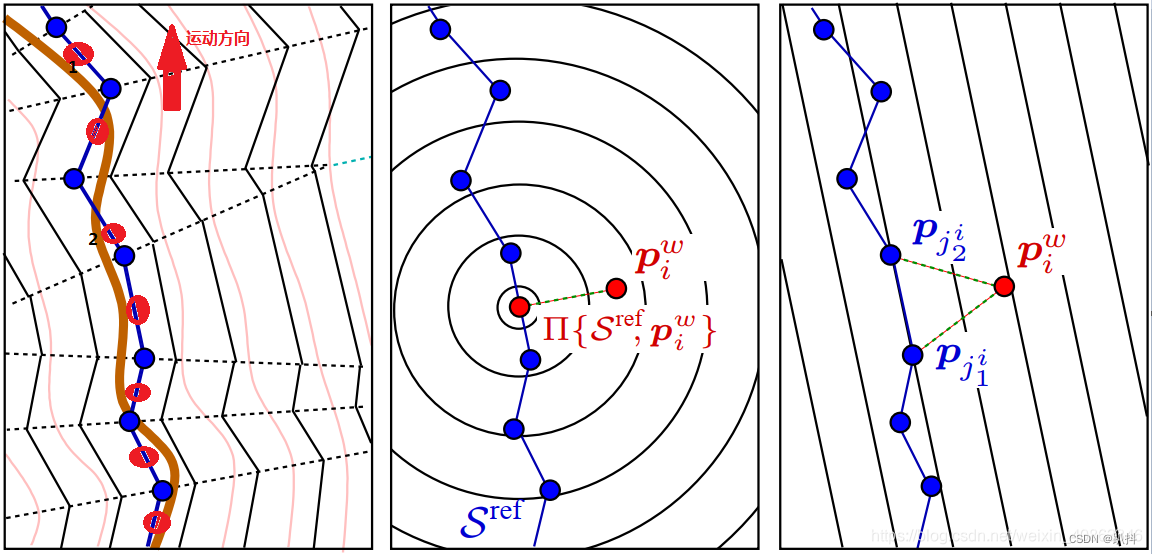
假设棕色那条线是实际场景中的墙,蓝色是t时刻的扫描点,红色的点是t+1时刻的扫描点,如果按照ICP的思想,t+1时刻的1点会匹配到t时刻的靠上的点(因为欧式距离更短),但是1点的正确匹配点应该是靠下的点,所以这个匹配就是错误的,所引起的额外的匹配误差是由于ICP本身的算法引起的。因为匹配算法强制的认为他们是空间中的同一个点,但是对于激光雷达,前后两帧的激光数据很有可能是打到不同的物体或者说是同一物体的不同部位(类似ICP在点云配准中,前后是匹配的),所以这是ICP算法的缺点。
PL-ICP算法的原理:
室内环境通常是结构化环境,即譬如墙壁等有众多规则的曲面,而激光数据实际是对实际环境中曲面的离散采样,因此,最好的误差尺度就是点到实际曲面的距离。我们目前通过传感器已经知晓激光点云数据,实际的重点就是对环境中曲面的恢复。PL-ICP 采用分段线性的方式近似替代曲面,从而获得激光点到实际曲面的距离。
所以最好的方法就是计算离最近邻两点组成的直线的距离,如下图:
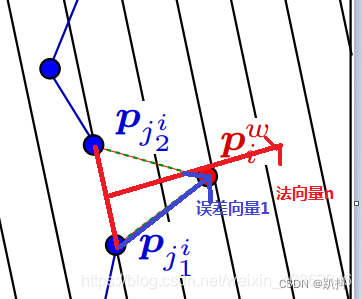
数学描述:

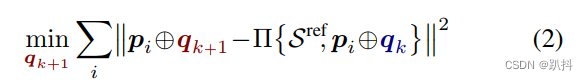
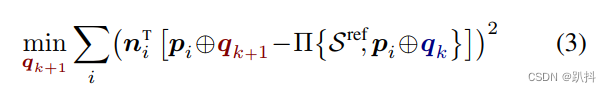
如(2)式,是ICP算法的目标函数数学表达式;(3)式PLICP算法的目标函数表达式,比ICP多了一个直线的法向量。
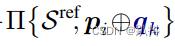 可以看做是t时刻的参考帧,
可以看做是t时刻的参考帧, 看做是k+1时刻经过R和t变化到t时刻的当前帧,这两个之间的差值是一个向量。那么ICP的算法求的就是误差向量1的模的平方,而PL-ICP算法就是秋误差向量1在法向量ni上的投影(也就是到直线的距离)。目标函数就是求所有这些距离和的最小值,从而得到R和t。
看做是k+1时刻经过R和t变化到t时刻的当前帧,这两个之间的差值是一个向量。那么ICP的算法求的就是误差向量1的模的平方,而PL-ICP算法就是秋误差向量1在法向量ni上的投影(也就是到直线的距离)。目标函数就是求所有这些距离和的最小值,从而得到R和t。
算法流程:

跟ICP的区别:

基于优化的匹配方法(Optimization-based Method)
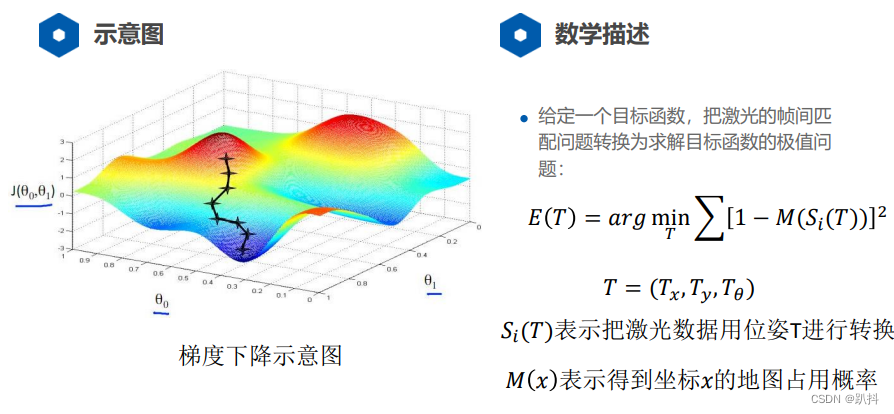
优化方法的求解

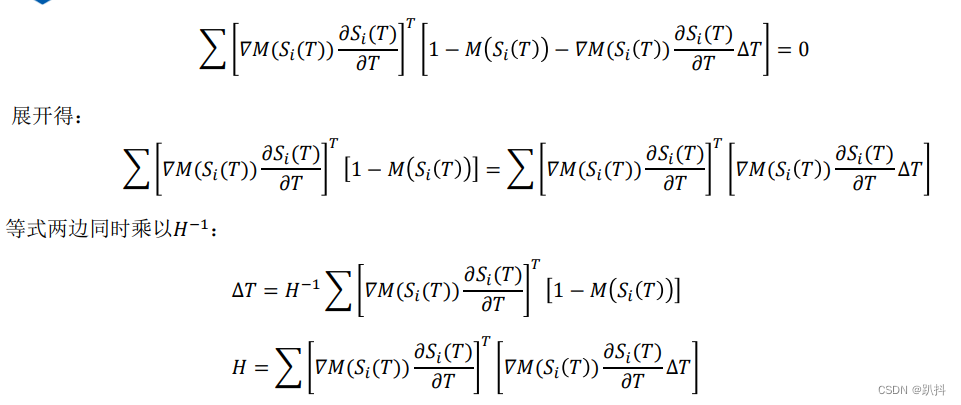

地图双线性插值
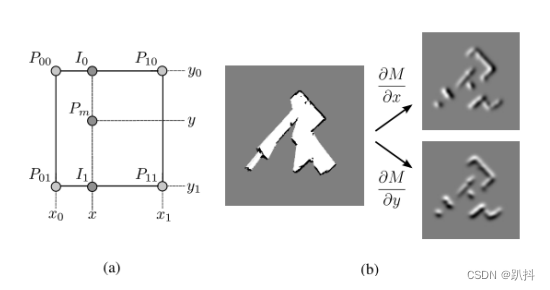
拉格朗日插值法——一维线性插值
插值的定义:

拉格朗日插值方法:
实现上述插值的一种方法,主要特点为把插值多项式表示成基函数的线性组合:
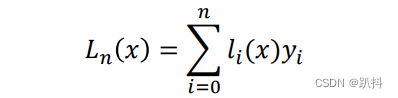
基函数li(x)满足以下条件:
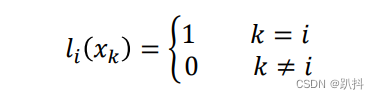
由于Ln(x)存在且唯一,所以只需要表示出Ln(x)的其中一种形式即可,因为各形式之间等价,表示的都是Ln(x)。
拉格朗日插值方法——基函数构造:

拉格朗日插值方法——双线性插值:
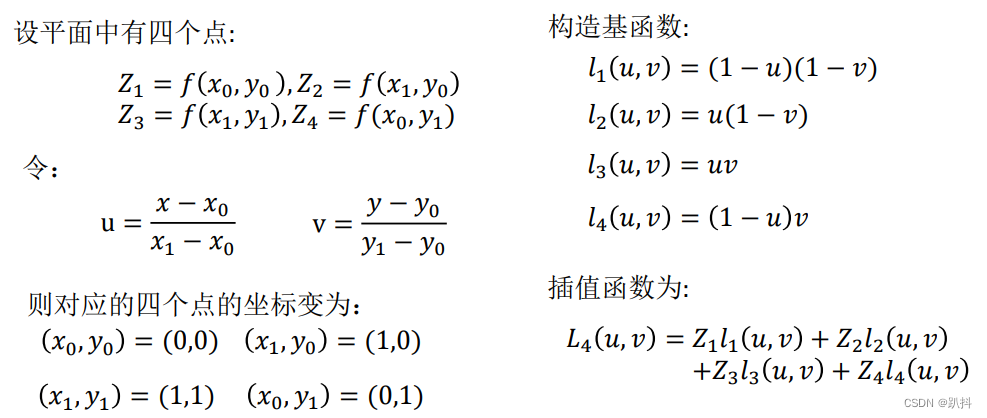
地图插值:
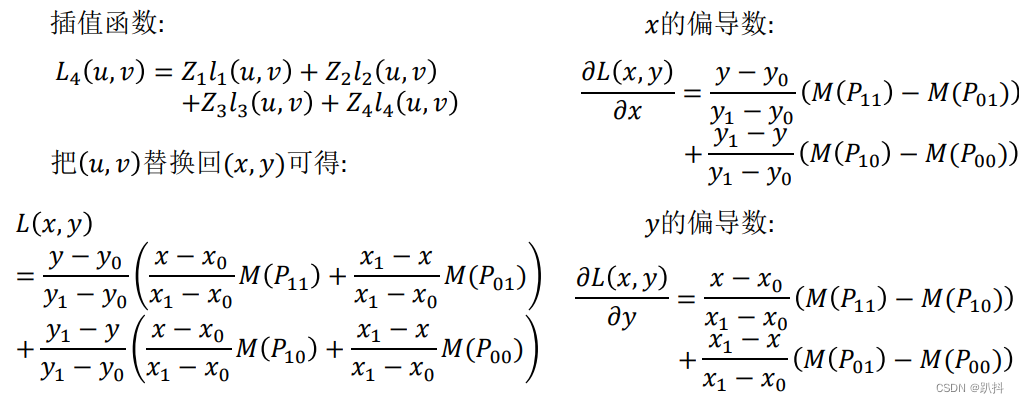
相关方法(Correlation-based Method)
帧间匹配似然场
- 高度非凸,存在很多的局部极值
- 对初值非常敏感
- 进行暴力匹配,排除初值影响
- 通过加速策略,降低计算量
- 计算位姿匹配方差

算法流程
- 构建似然场
- 在指定的搜索空间内进行暴力搜索,计算每一个位姿的得分
- 根据步骤2中位姿的最高得分,计算本次位姿匹配的方差

位姿搜索

分枝定界算法
- 常用的树形搜索剪枝算法
- 求解整数规划问题
- 解的数量为有限个
- 把最优解求解问题转换为树形搜索问题,根节点表示整个解空间,叶子节点表示具体的解,中间的节点表示解空间的某一部分子空间
分枝: 即根节点表示整个解空间空间,深度为1的节点表示解空间的子空间,深度为2的节点表示深度1空间的子空间,这样层层划分,直到划分到真实解,也就是叶子节点为止。
定界: 对于搜索树种的每一个节点,确定以该节点为根节点的子树的界。对于最小值问题,确定下界;对于最大值问题,确定上界。(SLAM中为上界)

分枝定界在相关方法的加速作用:


引用
点云配准方法–PLICP



)




课后练习答案(十四)(1))



![帮管家 CRM init 信息泄露漏洞复现 [附POC]](http://pic.xiahunao.cn/帮管家 CRM init 信息泄露漏洞复现 [附POC])






)