算法思想

从集合角度来分析DP问题
例如求最值、求个数

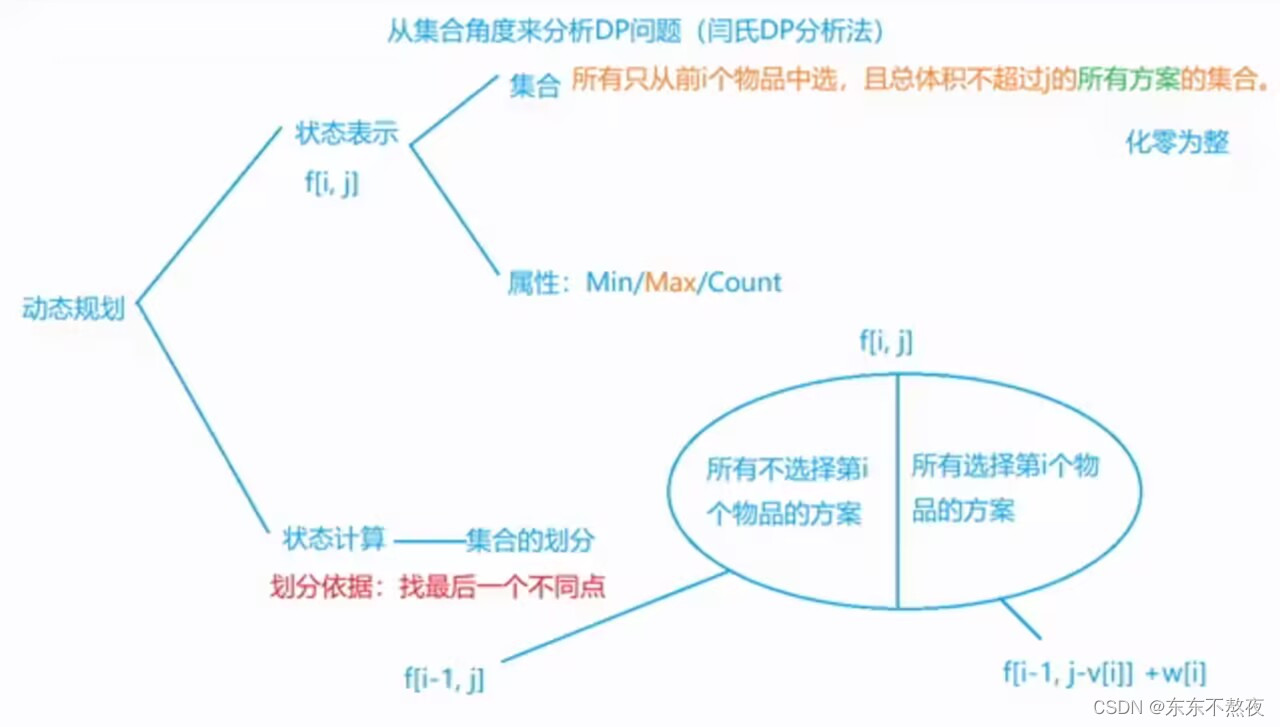
例题

1、01背包问题

题目信息

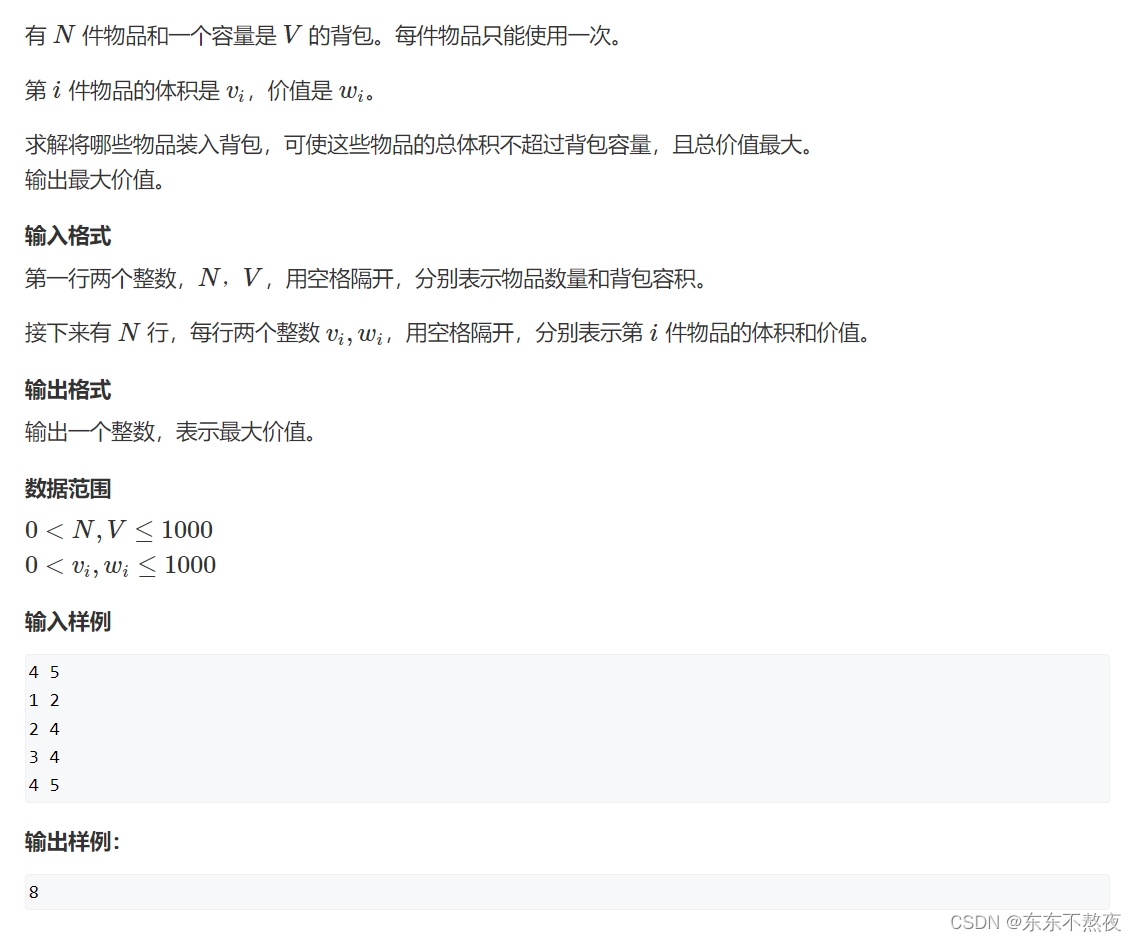
思路

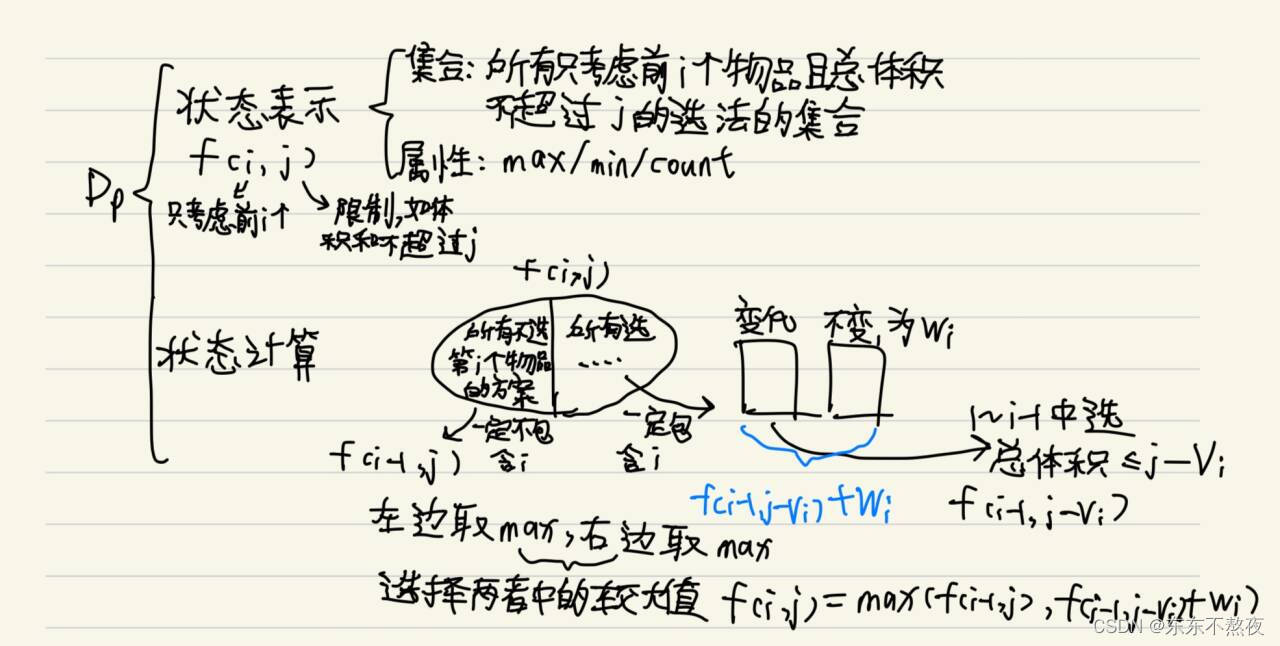
题解

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define maxsize 1010
using namespace std;int n,m;
int v[maxsize],w[maxsize];
int f[maxsize][maxsize];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];   //左半边的子集if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;return 0;
}

2、摘花生

题目信息

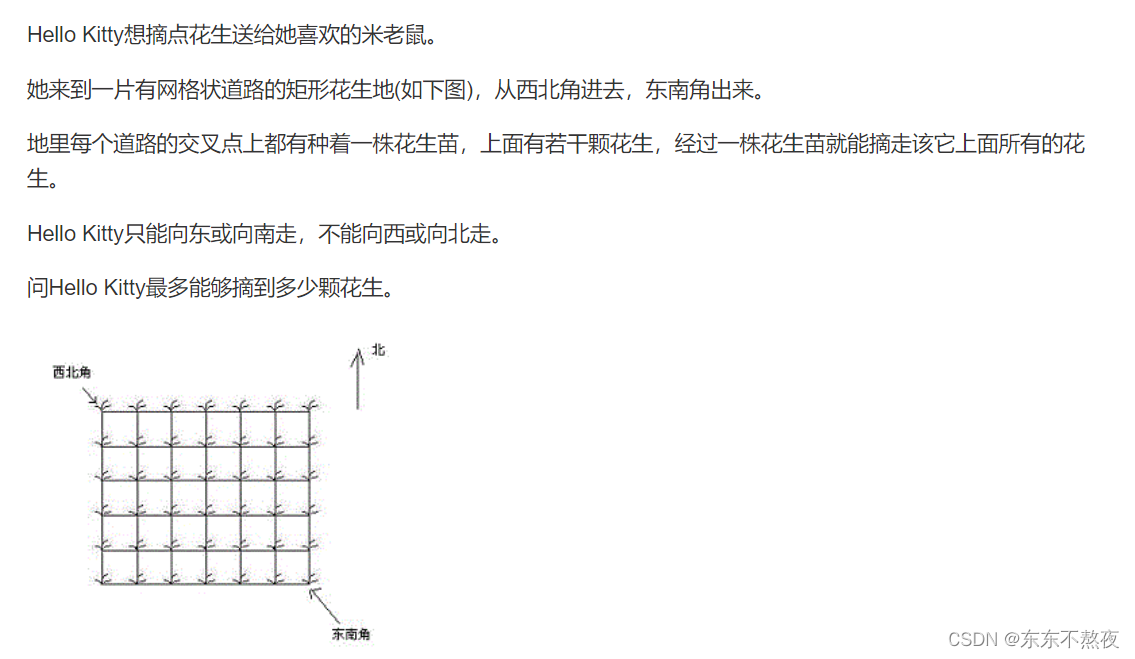
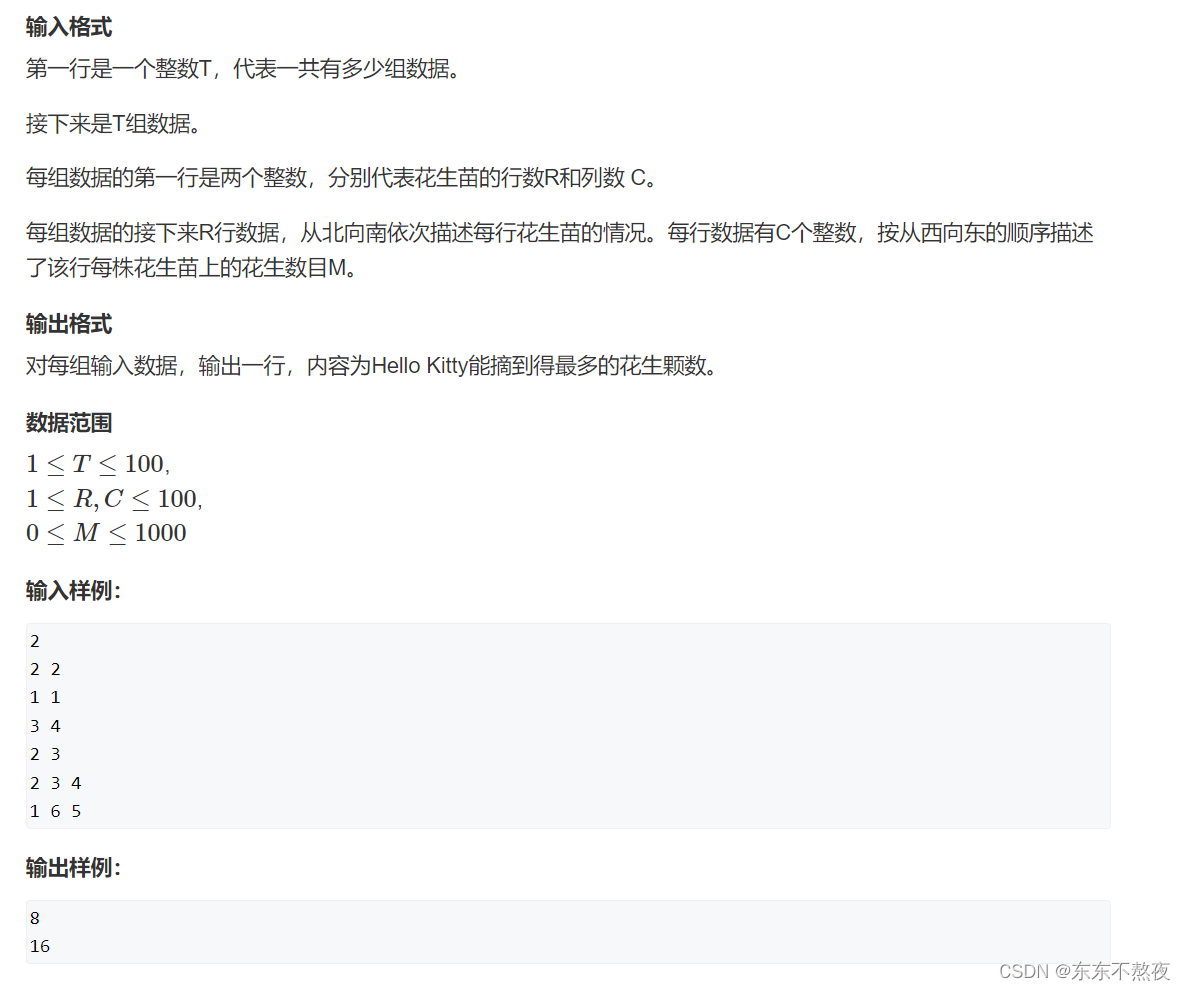
思路

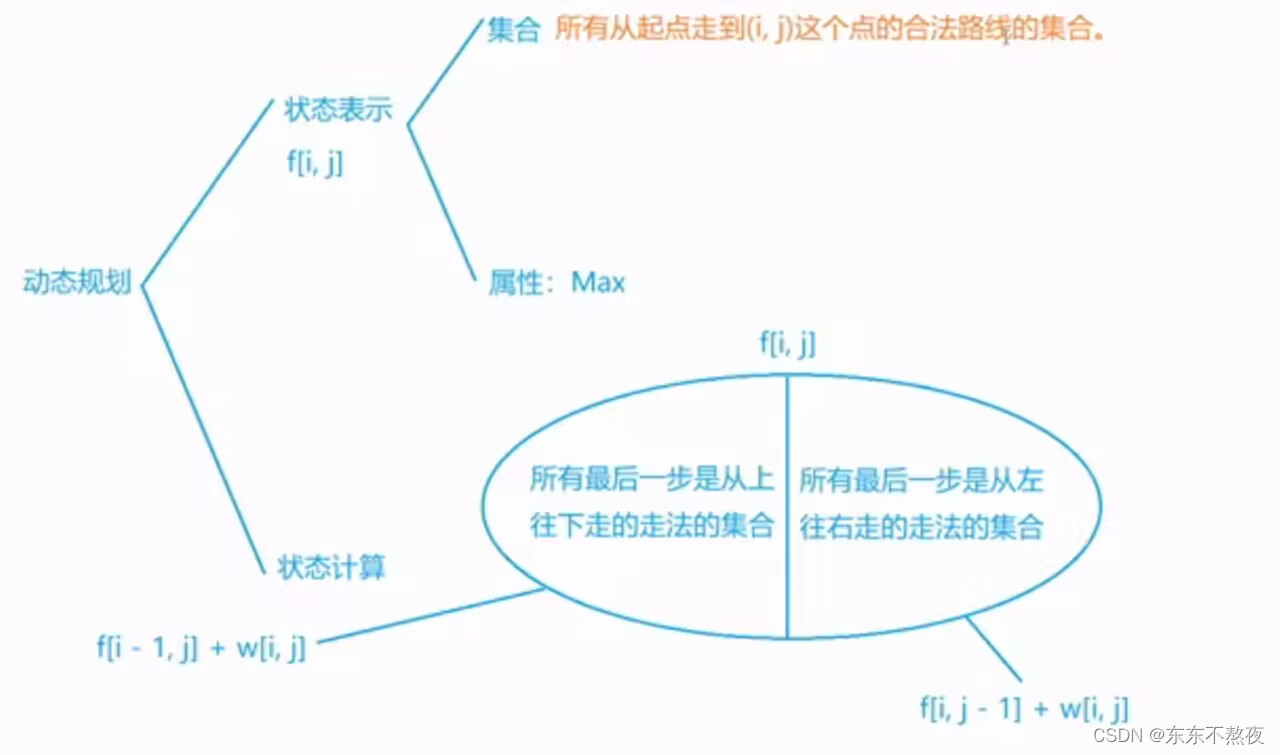
题解

#include <bits/stdc++.h>
#define int long long 
#define endl '\n'
#define maxsize 110
using namespace std;int t;
int w[maxsize][maxsize],f[maxsize][maxsize];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>t;for(int i=1;i<=t;i++){int a,b;cin>>a>>b;for(int x=1;x<=a;x++){for(int y=1;y<=b;y++){cin>>w[x][y];}}for(int x=1;x<=a;x++){for(int y=1;y<=b;y++){f[x][y]=max(f[x-1][y],f[x][y-1])+w[x][y];}}cout<<f[a][b]<<endl;}return 0;
}

3、最长上升子序列

题目信息

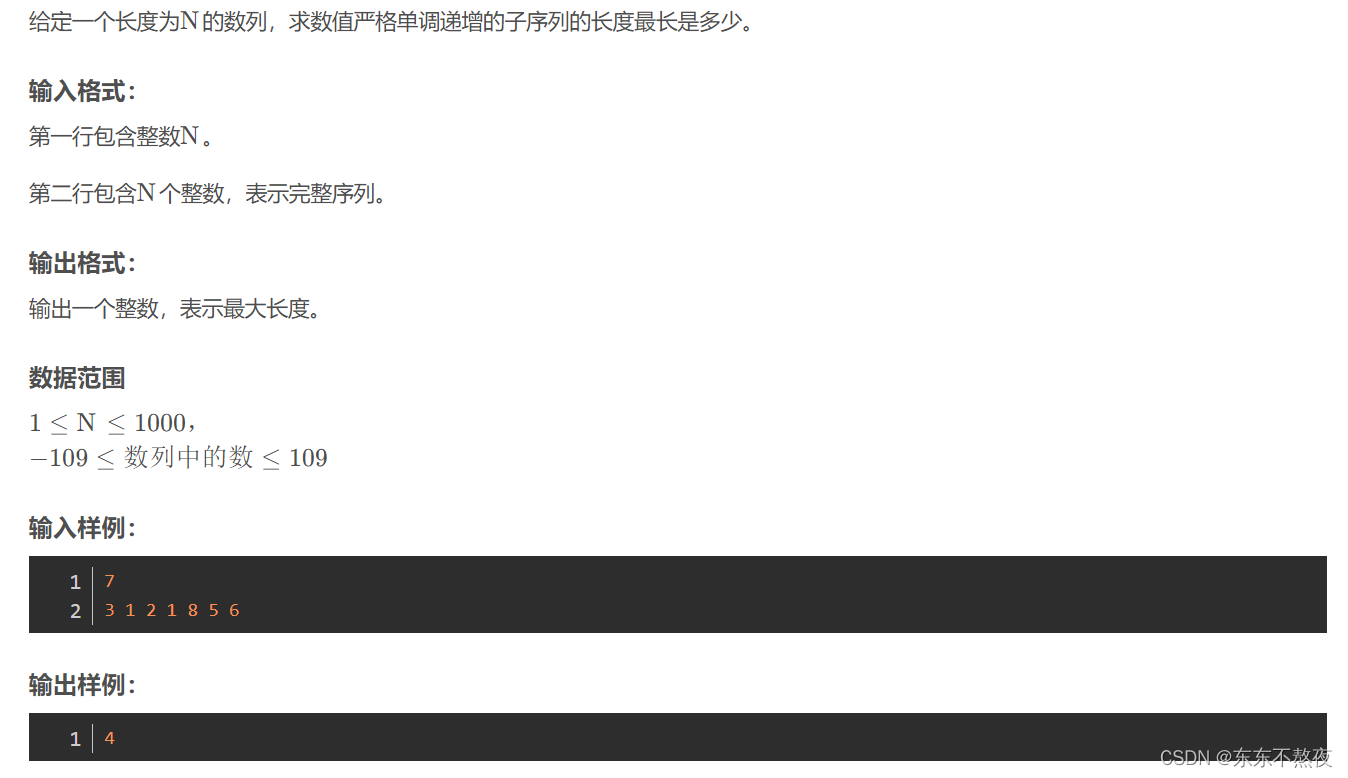
思路

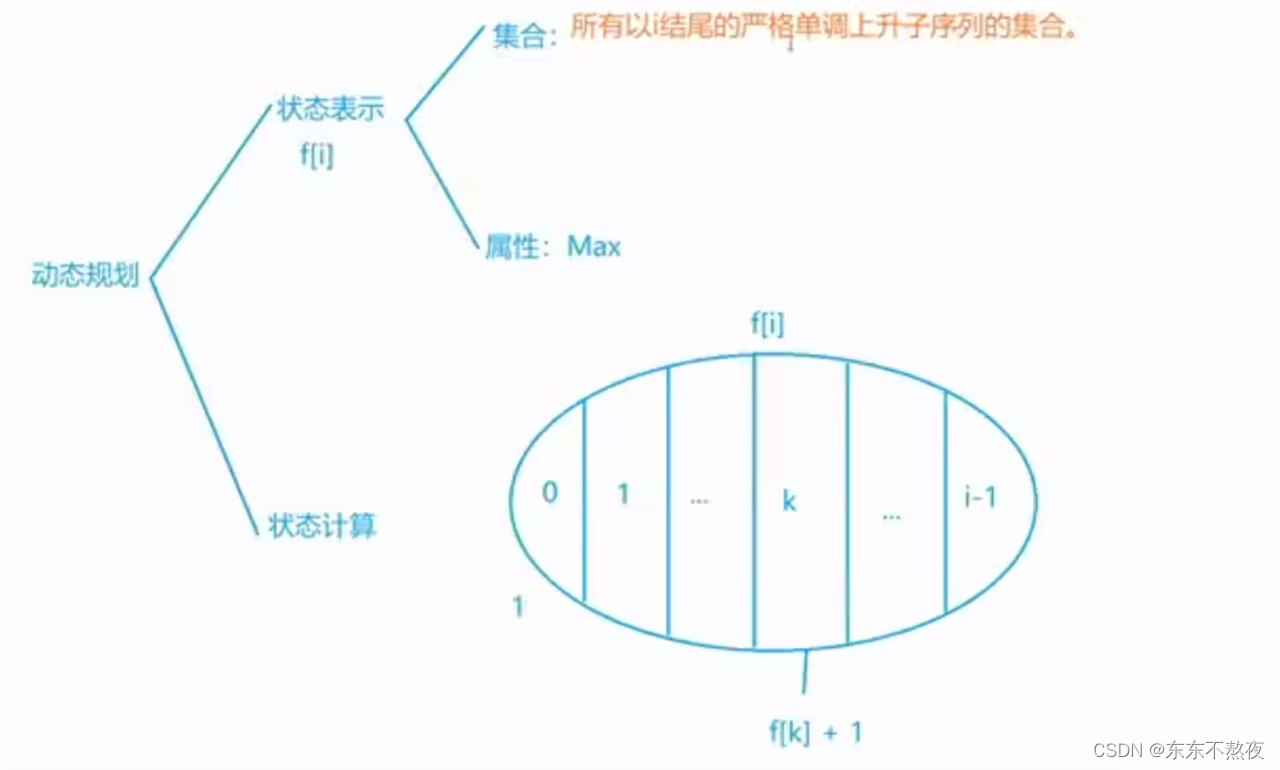
博主看到有一篇博客中的思路易于理解，复制如下：

	我们都知道，动态规划的一个特点就是当前解可以由上一个阶段的解推出， 由此，把我们要求的问题简化成一个更小的子问题。子问题具有相同的求解方式，只不过是规模小了而已。最长上升子序列就符合这一特性。我们要求n个数的最长上升子序列，可以求前n-1个数的最长上升子序列，再跟第n个数进行判断。求前n-1个数的最长上升子序列，可以通过求前n-2个数的最长上升子序列……直到求前1个数的最长上升子序列，此时LIS当然为1。让我们举个例子：求 2 7 1 5 6 4 3 8 9 的最长上升子序列。我们定义d(i) (i∈[1,n])来表示前 i 个数以A[ i ]结尾的最长上升子序列长度。前1个数 d(1)=1 子序列为2；前2个数 7前面有2小于7 d(2)=d(1)+1=2 子序列为2 7前3个数 在1前面没有比1更小的，1自身组成长度为1的子序列 d(3)=1 子序列为1前4个数 5前面有2小于5 d(4)=d(1)+1=2 子序列为2 5前5个数 6前面有2 5小于6 d(5)=d(4)+1=3 子序列为2 5 6前6个数 4前面有2小于4 d(6)=d(1)+1=2 子序列为2 4前7个数 3前面有2小于3 d(3)=d(1)+1=2 子序列为2 3前8个数 8前面有2 5 6小于8 d(8)=d(5)+1=4 子序列为2 5 6 8前9个数 9前面有2 5 6 8小于9 d(9)=d(8)+1=5 子序列为2 5 6 8 9d(i)=max{d(1),d(2),……,d(i)} 我们可以看出这9个数的LIS为d(9)=5总结一下，d(i) 就是找以A[ i ]结尾的，在A[ i ]之前的最长上升子序列+1，即前 i 个数的 LIS 长度 + 1。当A[ i ]之前没有比A[ i ]更小的数时，d(i) = 1。所有的d(i)里面最大的那个就是最长上升子序列。其实说的通俗点，就是每次都向前找比它小的数和比它大的数的位置，将第一个比它大的替换掉，这样操作虽然LIS序列的具体数字可能会变，但是很明显LIS长度还是不变的，因为只是把数替换掉了，并没有改变增加或者减少长度。但是我们通过这种方式是无法求出最长上升子序列具体是什么的，这点和最长公共子序列不同。原文链接：https://blog.csdn.net/lxt_Lucia/article/details/81206439

题解

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define maxsize 1010
using namespace std;int n;
int a[maxsize];
int f[maxsize];   //用来存储到f(i)最长子序列的个数signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<=n;i++) cin>>a[i];int res=0;for(int i=1;i<=n;i++){f[i]=1;for(int j=1;j<i;j++){if(a[i]>a[j]){f[i]=max(f[i],f[j]+1);}}res=max(res,f[i]);}cout<<res<<endl;return 0;
}

题目练习

1、地宫取宝

题目信息

思路

题解

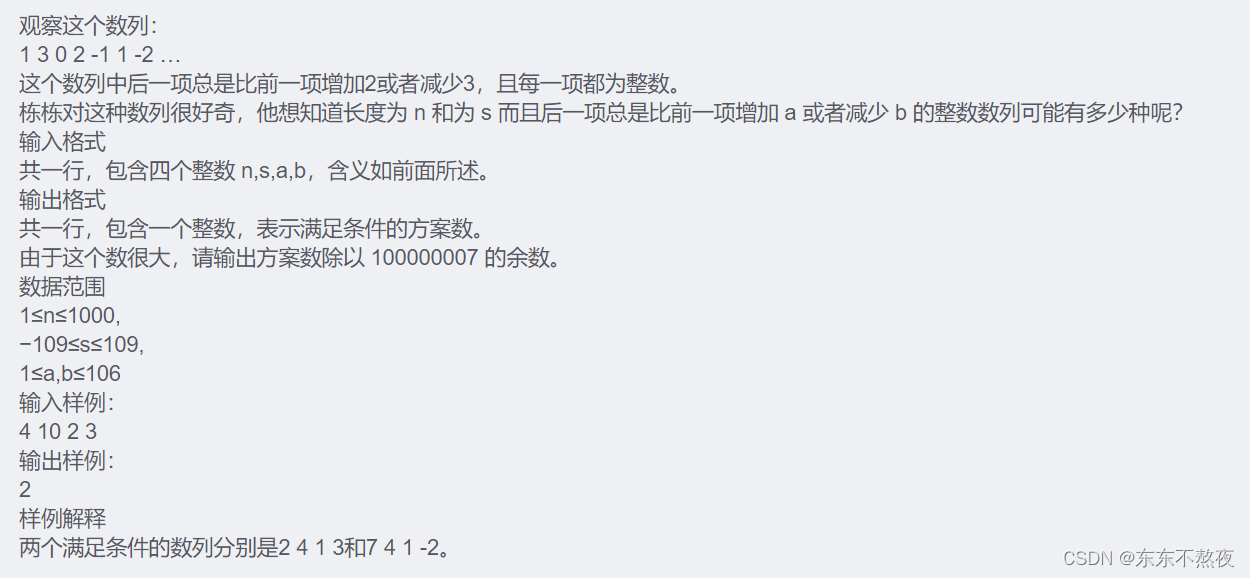
2、波动数列

题目信息

思路

题解