"The harder the conflict, the more glorious the triumph."
- Thomas Paine

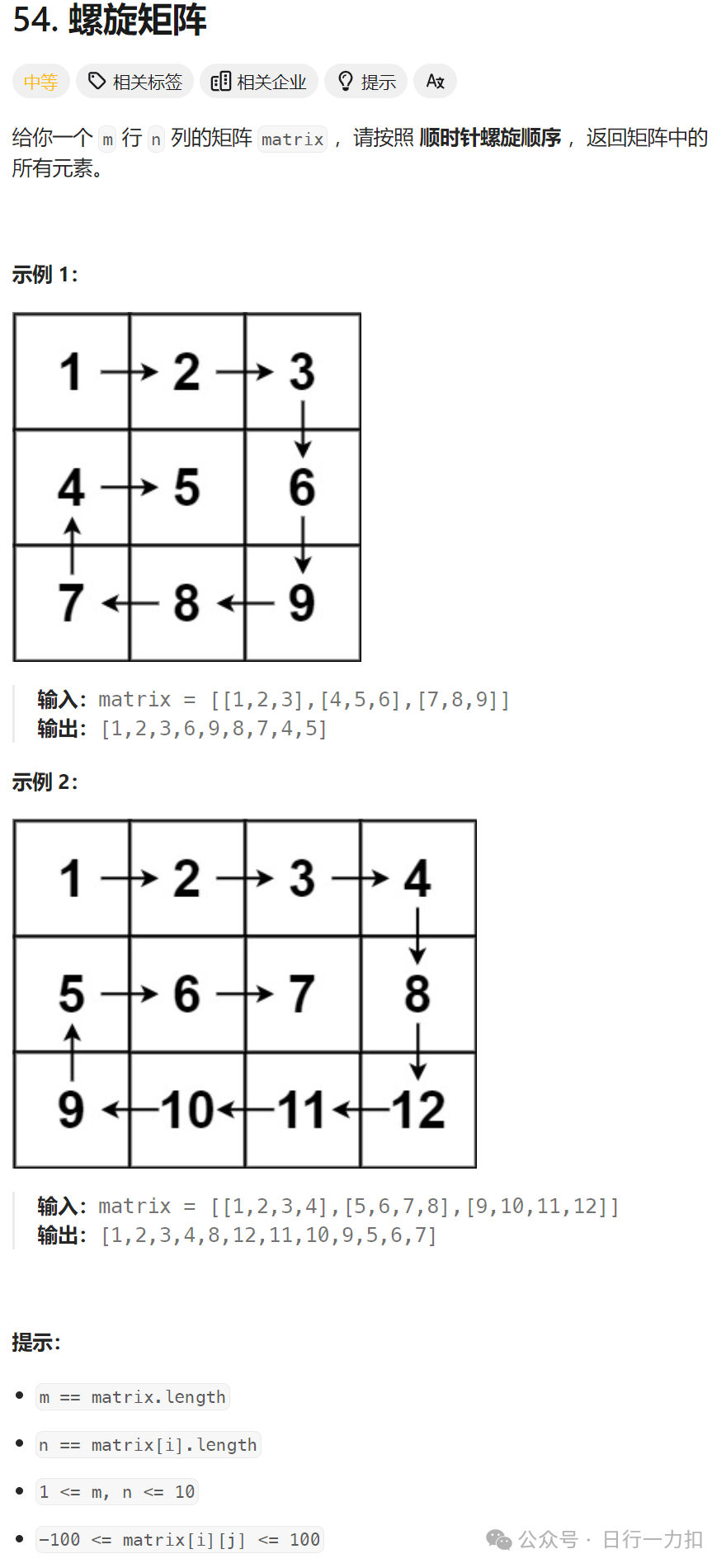
1. 题目描述
2. 题目分析与解析
2.1 思路一
看到题目,先仔细观察矩阵,题目要求我们给出顺时针遍历的结果即可,我们根据矩阵可以看出,首先遍历的是向右的行,然后是向下的列,在之后是向左的行,最后是向上的列,以此循环。那么我们按照普通人看见一个这样的矩阵和题目的要求,他会怎么做?那就是尝试按照题目要求的顺序,不断走下去把结果列出即可。
而这个过程人在尝试的遍历的获取结果的时候,是不是还得注意边界的问题,即什么时候需要转弯,什么时候停止(虽然一个人在真正完成任务时可能并没有意识到考虑了这些因素,那只是因为还不够复杂,当更加复杂的矩阵呈现在人面前,人就会尝试找到这两个问题的答案,然后按照其规则移动)?实际上这就是人的一种算法,而计算机想要模拟人的这种解决问题的方式就需要解决人需要解决的问题:
-
什么时候需要转弯?
-
什么时候停止?
不管怎么样对于一个矩阵A=【n, m】,最先走的肯定是第一行,然后当走到A【0,m - 1】时,就需要转弯了,这时候就是不断变大行也就是从A【1,m - 1】到A【n - 1, m - 1】,然后继续转弯,从A【n - 1, m - 2】到 A【n - 1, 0】,再转弯,从A【n - 2, 0】到A【1,0】,这样就完成了第一次循环。
可以发现,转弯的条件就是:
当遍历行时,当列到达边界就需要转弯
当遍历列时,当行达到边界就需要转弯
同时需要注意,在每遍历完一行或者一列时,边界也是需要不断收缩的
现在再回过头再看看:(边界是【0,0】【n - 1,m - 1】表示左上角和右下角的元素下标)
-
开始的边界是【0,0】【n - 1,m - 1】,最先走的肯定是第一行,然后当走到A【0,m - 1】时,就需要转弯了,此时需要收缩边界变为【1,0】【n - 1,m - 1】

-
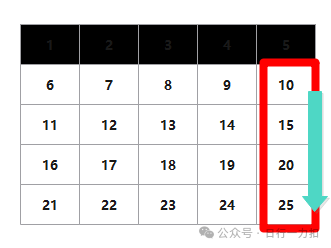
开始的边界是【1,0】【n - 1,m - 1】,不断变大行也就是从A【1,m - 1】到A【n - 1, m - 1】,然后继续转弯,此时需要收缩边界变为【1,0】【n - 1, m - 2】
-
开始的边界是【1,0】【n - 1,m - 2】,不断变小列也就是从A【n - 1, m - 2】到A【n - 1, 0】,然后继续转弯,此时需要收缩边界变为【1,0】【n - 2, m - 2】

-
开始的边界是【1,0】【n - 2, m - 2】,不断变大行也就是从A【n - 2,0】到A【1, 0】,然后继续转弯,此时需要收缩边界变为【1,1】【n - 2, m - 2】

可以看出,当遍历行时,到达终点需要收缩行,当遍历列时,达到终点需要收缩列。
所以我们是不是就可以这样一层一层的遍历,直到边界收缩到一个元素,也就是左上角边界等于右下角边界停止?
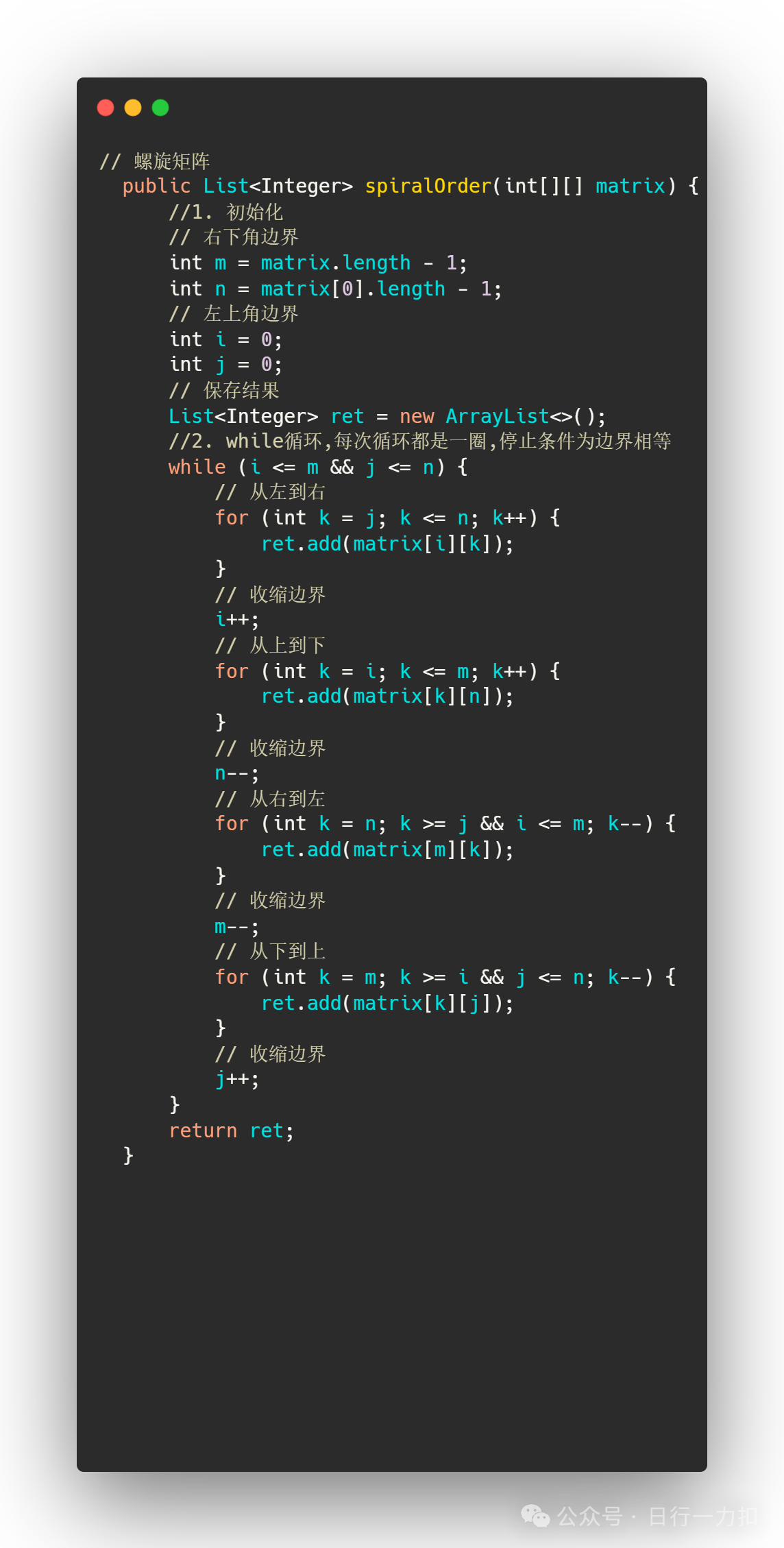
代码思路:
-
初始化边界,【0,0】和【行数 - 1,列数 - 1】
-
while循环,停止条件为边界相等
-
走每一个边,走完一个边需要收缩边界并且转弯,并且在走该边之前要先判断是否以及越界
3. 代码实现
4. 相关复杂度分析
时间复杂度分析
-
总的时间复杂度为 O(m*n),其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度分析
-
额外空间:除了存储结果的列表外,代码没有使用额外的数据结构,除了输出数组以外,空间复杂度是常数O(1)。









)



)

)
)
)
)
