文章目录
- II. SYSTEM MODEL AND PROBLEM FORMULATION
- C. Problem Formulation
- III. PROPOSED ALGORITHM
- A. Alternating Optimization
- B. Solution for Problem (P2-m)
- APPENDIX
II. SYSTEM MODEL AND PROBLEM FORMULATION
C. Problem Formulation
为了揭示支持 MA 的MIMO通信的基本容量限制,我们假设在发送端和接收端都有完美的CSI。MIMO信道容量由下式给出
C = max Q : Tr ( Q ) ≤ P , Q ⪰ 0 log 2 det ( I M + 1 σ 2 H ( r ~ ) Q H ( r ~ ) H ) \begin{equation*}C=\max\limits_{\boldsymbol{Q}:\text{Tr}(\boldsymbol{Q})\leq \mathrm{P},\boldsymbol{Q}\succeq \boldsymbol{0}}\log_{2}\det\left(\boldsymbol{I}_{M}+\frac{1}{\sigma^{2}}\boldsymbol{H}(\tilde{\boldsymbol{r}})\boldsymbol{QH}(\tilde{\boldsymbol{r}})^{H}\right)\tag {5}\end{equation*} C=Q:Tr(Q)≤P,Q⪰0maxlog2det(IM+σ21H(r~)QH(r~)H)(5)
我们的目标是通过联合优化MA位置 r ~ \tilde{\boldsymbol{r}} r~ 和发射协方差矩阵 Q \boldsymbol{Q} Q 来最大化MA- MIMO信道的容量,同时要遵守MA-位置的最小距离约束和发射机的和功率约束。因此,该优化问题被表述为
( P 1 ) max r ~ , Q log 2 det ( I M + 1 σ 2 H ( r ~ ) Q H ( r ~ ) H ) s . t . r ~ ∈ C , ∥ r k − r l ∥ 2 ≥ D , k , l = 1 , 2 , … , M , k ≠ l , Tr ( Q ) ≤ P , Q ⪰ 0 . \begin{align*}(\mathrm{P}1) \max\limits_{\tilde{\boldsymbol{r}},\boldsymbol{Q}} &\quad \log_{2}\det\left(\boldsymbol{I}_{M}+\frac{1}{\sigma^{2}}\boldsymbol{H}(\tilde{\boldsymbol{r}})\boldsymbol{QH}(\tilde{\boldsymbol{r}})^{H}\right)\tag{6a}\\ \mathrm{s}.\mathrm{t}. &\quad \tilde{\boldsymbol{r}}\in \mathcal{C},\tag{6b}\\ &\quad \Vert \boldsymbol{r}_{k}-\boldsymbol{r}_{l} \Vert_{2}\geq D, k, l=1,2, \ldots, M,\ k\neq l,\tag{6c}\\ &\quad \text{Tr} (\boldsymbol{Q})\leq \mathrm{P}, \tag{6d}\\ &\quad \boldsymbol{Q}\succeq \boldsymbol{0}. \tag{6e}\end{align*} (P1)r~,Qmaxs.t.log2det(IM+σ21H(r~)QH(r~)H)r~∈C,∥rk−rl∥2≥D,k,l=1,2,…,M, k=l,Tr(Q)≤P,Q⪰0.(6a)(6b)(6c)(6d)(6e)
注意,问题(P1)是一个非凸优化问题,因为目标函数在上是非凹的,关于MA位置 r ~ \tilde{\boldsymbol{r}} r~, (6c)中的最小距离约束是非凸的。此外,在(P1)的目标函数中,传输协方差矩阵 Q \boldsymbol{Q} Q 与 r ~ \tilde{\boldsymbol{r}} r~ 相耦合,这使得(P1)具有解决的挑战性。
log-determinant 是很容易证明是凹函数,详细的证明过程可以参考这个网站。但是 H ( r ~ ) \boldsymbol{H}(\tilde{\boldsymbol{r}}) H(r~) 是无法确定的。因此无法确定凹凸性。
III. PROPOSED ALGORITHM
A. Alternating Optimization
- Optimization of Q \boldsymbol{Q} Q with given { r m } m = 1 M \{\boldsymbol{r}_{m}\}_{m=1}^{M} {rm}m=1M
注意,在给定 H ( r ~ ) \boldsymbol{H}(\tilde{\boldsymbol{r}}) H(r~) 的情况下,(P1)是 Q \boldsymbol{Q} Q 上的一个凸优化问题,最优解由本征模传输(eigenmode transmission)给出。
- Optimization of r m \boldsymbol{r}_{m} rm with given Q \boldsymbol{Q} Q and { r k , k ≠ m } k = 1 M \{\boldsymbol{r}_{k},k\neq m\}_{k=1}^{M} {rk,k=m}k=1M
f ( r ~ ) ≜ log 2 det ( I M + 1 σ 2 H ( r ~ ) Q H ( r ~ ) H ) = log 2 det ( I M + 1 σ 2 W ( r ~ ) W ( r ~ ) H ) = ( a ) log 2 det ( I N + 1 σ 2 W ( r ~ ) H W ( r ~ ) ) = log 2 det ( I N + 1 σ 2 ∑ m = 1 M w ( r m ) w ( r m ) H ) , ≜ \begin{align*}f(\tilde{\boldsymbol{r}}) & {{ } \triangleq} \log_{2}\det\left(\boldsymbol{I}_{M}+\frac{1}{\sigma^{2}} \boldsymbol{H}(\tilde{\boldsymbol{r}})\boldsymbol{QH}(\tilde{\boldsymbol{r}})^{H}\right) \tag{9}\\ & = \log_{2}\det\left(\boldsymbol{I}_{M}+\frac{1}{\sigma^{2}}\boldsymbol{W}(\tilde{\boldsymbol{r}})\boldsymbol{W}(\tilde{\boldsymbol{r}})^{H}\right)\\ & \overset{(\mathrm{a})}{=} \log_{2}\det\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}}\boldsymbol{W}(\tilde{\boldsymbol{r}})^{H}\boldsymbol{W}(\tilde{\boldsymbol{r}})\right)\\ & = \log_{2}\det\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}} \sum\limits_{m=1}^{M}\boldsymbol{w}(\boldsymbol{r}_{m})\boldsymbol{w}(\boldsymbol{r}_{m})^{H}\right),\end{align*}\triangleq f(r~)≜log2det(IM+σ21H(r~)QH(r~)H)=log2det(IM+σ21W(r~)W(r~)H)=(a)log2det(IN+σ21W(r~)HW(r~))=log2det(IN+σ21m=1∑Mw(rm)w(rm)H),(9)≜
这一步非常聪明,将信道容量分解为和每个 w ( r m ) \boldsymbol{w}(\boldsymbol{r}_{m}) w(rm) 之间的关系。
其中(a)标记的等式成立,因为对于 A ∈ C p × q \boldsymbol{A}\in \mathbb{C}^{p\times q} A∈Cp×q 和 B ∈ C q × p \boldsymbol{B}\in \mathbb{C}^{q\times p} B∈Cq×p, det ( I p + A B ) = det ( I q + B A ) \det(\boldsymbol{I}_{p}+ \boldsymbol{AB})=\det(\boldsymbol{I}_{q}+\boldsymbol{BA}) det(Ip+AB)=det(Iq+BA)。请注意,(9)所示(P1)的等效目标函数以显式形式解耦了所有M MAs的位置变量,即 { r m } m = 1 M \{\boldsymbol{r}_{m}\}_{m=1}^{M} {rm}m=1M,这便于后续对 r m \boldsymbol{r}_{m} rm 进行优化。
从 W ( r ~ ) H \boldsymbol{W}(\tilde{\boldsymbol{r}})^{H} W(r~)H 中去除 w ( r m ) \boldsymbol{w}(\boldsymbol{r}_{m}) w(rm),并用 W m H \boldsymbol{W}_{m}^{H} WmH 表示剩余的 N × ( M − 1 ) N\times (M-1) N×(M−1) 子矩阵 W m H = [ w ( r 1 ) , w ( r 2 ) , … , w ( r m − 1 ) , w ( r m + 1 ) , … , w ( r M ) ] \boldsymbol{W}_{m}^{H} = [\boldsymbol{w}(\boldsymbol{r}_{1}),\boldsymbol{w}(\boldsymbol{r}_{2}),\ldots,\boldsymbol{w}(\boldsymbol{r}_{m-1}),\boldsymbol{w}(\boldsymbol{r}_{m+1}),\ldots,\boldsymbol{w}(\boldsymbol{r}_{M})] WmH=[w(r1),w(r2),…,w(rm−1),w(rm+1),…,w(rM)]。这样,(P1)在(9)中的目标函数可以重写为[11]
f ˉ ( r m ) = log 2 det ( I N + 1 σ 2 ( W m H W m + w ( r m ) w ( r m ) H ) ) = ( b 1 ) log 2 det ( I N + 1 σ 2 ( I N + 1 σ 2 W m H W m ) − 1 w ( r m ) w ( r m ) H ) + log 2 det ( I N + 1 σ 2 W m H W m ) = ( b 2 ) log 2 ( 1 + 1 σ 2 w ( r m ) H ( I N + 1 σ 2 W m H W m ) − 1 w ( r m ) ) + log 2 det ( I N + 1 σ 2 W m H W m ) , \begin{align*}&\bar{f}(\boldsymbol{r}_{m})= \log_{2}\det\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}}\left(W_{m}^{H}\boldsymbol{W}_{m}+\boldsymbol{w}(\boldsymbol{r}_{m})\boldsymbol{w}(\boldsymbol{r}_{m})^{H}\right)\right)\\ &\overset{(\mathrm{b}_{1})}{=} \log_{2}\det\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}}\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}}\boldsymbol{W}_{m}^{H}\boldsymbol{W}_{m}\right)^{-1}\boldsymbol{w}(\boldsymbol{r}_{m})\boldsymbol{w}(\boldsymbol{r}_{m})^{H}\right)\\ &\qquad+ \log_{2}\det\left(I_{N}+\frac{1}{\sigma^{2}}\boldsymbol{W}_{m}^{H}\boldsymbol{W}_{m}\right)\\ &\overset{(b_{2})}{=} \log_{2}\left(1+\frac{1}{\sigma^{2}}\boldsymbol{w}(\boldsymbol{r}_{m})^{H}\left(I_{N}+\frac{1}{\sigma^{2}}\boldsymbol{W}_{m}^{H}\boldsymbol{W}_{m}\right)^{-1}\boldsymbol{w}(\boldsymbol{r}_{m})\right)\\ &\qquad+ \log_{2}\det\left(\boldsymbol{I}_{N}+\frac{1}{\sigma^{2}}\boldsymbol{W}_{m}^{H}\boldsymbol{W}_{m}\right), \tag{10}\end{align*} fˉ(rm)=log2det(IN+σ21(WmHWm+w(rm)w(rm)H))=(b1)log2det(IN+σ21(IN+σ21WmHWm)−1w(rm)w(rm)H)+log2det(IN+σ21WmHWm)=(b2)log2(1+σ21w(rm)H(IN+σ21WmHWm)−1w(rm))+log2det(IN+σ21WmHWm),(10)
这一步也是非常的巧妙,将不相关的 W m H \boldsymbol{W}_{m}^{H} WmH 全都提取了出来。
因此,优化 r m \boldsymbol{r}_{m} rm 的子问题可以表示为 ( P 2 − m ) max r m f ( r m ) H B m f ( r m ) s . t . r m ∈ C , ∥ r m − r k ∥ 2 ≥ D , k = 1 , 2 , … , M , k ≠ m . \begin{align*}(\mathrm{P}2-\mathrm{m}) \max_{\boldsymbol{r}_{m}}\ & \boldsymbol{f}(\boldsymbol{{r}}_{m})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m})\tag{12a}\\ \mathrm{s}.\mathrm{t}.\quad & \boldsymbol{r}_{m}\in \mathcal{C}, \tag{12b}\\ & \Vert \boldsymbol{r}_{m}-\boldsymbol{r}_{k} \Vert_{2}\geq D, k=1,2, \ldots, M,\quad k\neq m.\tag{12c}\end{align*} (P2−m)rmmax s.t.f(rm)HBmf(rm)rm∈C,∥rm−rk∥2≥D,k=1,2,…,M,k=m.(12a)(12b)(12c)
B. Solution for Problem (P2-m)
回想一下,任何凸函数在任意点上的一阶泰勒展开都是全局下界。在SCA的第 i i i 次迭代中,给定局部点边缘,我们得到 f ( r m ) H B m f ( r m ) \boldsymbol{f}(\boldsymbol{r}_{m})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m}) f(rm)HBmf(rm) 的下界为[12]
g ( r m ) = f ( r m ) H B m f ( r m ) ≥ f ( r m i ) H B m f ( r m i ) + 2 Re { f ( r m i ) H B m ( f ( r m ) − f ( r m i ) ) } = 2 Re { f ( r m i ) H B m f ( r m ) } ⏟ g ˉ ( r m ) − f ( r m i ) H B m f ( r m ) ⏟ constant , \begin{align*}g(\boldsymbol{r}_{m}) & =\boldsymbol{f}(\boldsymbol{r}_{m})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m})\tag{13}\\ & \geq \boldsymbol{f}(\boldsymbol{r}_{m}^{i})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m}^{i})+\\ &\quad 2\text{Re}\{\boldsymbol{f}(\boldsymbol{r}_{m}^{i})^{H}\boldsymbol{B}_{m}(\boldsymbol{f}(\boldsymbol{r}_{m})-\boldsymbol{f}(\boldsymbol{r}_{m}^{i}))\}\\ & =2\underbrace{\text{Re}\{\boldsymbol{f}(\boldsymbol{r}_{m}^{i})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m})\}}_{\bar{g}(\boldsymbol{r}_{m})}-\underbrace{\boldsymbol{f}(\boldsymbol{r}_{m}^{i})^{H}\boldsymbol{B}_{m}\boldsymbol{f}(\boldsymbol{r}_{m})}_{\text{constant}},\end{align*} g(rm)=f(rm)HBmf(rm)≥f(rmi)HBmf(rmi)+2Re{f(rmi)HBm(f(rm)−f(rmi))}=2gˉ(rm) Re{f(rmi)HBmf(rm)}−constant f(rmi)HBmf(rm),(13)
虽然 g ˉ ( r m ) \bar{g}(\boldsymbol{r}_{m}) gˉ(rm) 是 f ( r m ) \boldsymbol{f}(\boldsymbol{r}_{m}) f(rm) 上的线性函数,但在 r m \boldsymbol{r}_{m} rm 上仍然不是凹的,也不是凸的。因此,我们不能仅仅通过 g ˉ ( r m ) \bar{g}(\boldsymbol{r}_{m}) gˉ(rm) 的一阶泰勒展开来构造目标函数的下限代理函数。 Alternatively,我们用二阶泰勒展开构造一个局部逼近目标函数的代理函数。利用附录a给出的推导式,分别表示用 ∇ g ˉ ( r m ) ∈ R 2 \nabla\bar{g}(\boldsymbol{r}_{m})\in \mathbb{R}^{2} ∇gˉ(rm)∈R2 和 ∇ 2 g ˉ ( r m ) ∈ R 2 × 2 \nabla^{2}\bar{g}(\boldsymbol{r}_{m})\in \mathbb{R}^{2\times 2} ∇2gˉ(rm)∈R2×2 表示的梯度向量和Hessian矩阵,然后构造一个正实数 δ m \delta_{m} δm,用附录b给出的封闭表达式使得 δ m I 2 ⪰ ∇ 2 g ˉ ( r m ) \delta_{m}\boldsymbol{I}_{2}\succeq\nabla^{2}\bar{g}(\boldsymbol{r}_{m}) δmI2⪰∇2gˉ(rm),从而根据泰勒定理,我们可以找到一个二次代函数,使目标函数 g ˉ ( r m ) \bar{g}(\boldsymbol{r}_{m}) gˉ(rm) 全局下界为
g ˉ ( r m ) ≥ g ˉ ( r m i ) + ∇ g ˉ ( r m i ) T ( r m − r m i ) − δ m 2 ( r m − r m i ) T ( r m − r m i ) = − δ m 2 r m T r m + ( ∇ g ˉ ( r m i ) + δ m r m i ) T r m ⏟ g ~ ( r m ) + g ˉ ( r m i ) − δ m 2 ( r m i ) T r m i ⏟ constant . \begin{align*}\bar{g}(\boldsymbol{r}_{m}) & \geq \bar{g}(\boldsymbol{r}_{m}^{i}) + \nabla\bar{g}(\boldsymbol{r}_{m}^{i})^{T}(\boldsymbol{r}_{m}- \boldsymbol{r}_{m}^{i})-\tag{14}\\ &\quad \frac{\delta _m}{2}(\boldsymbol{r}_{m}- \boldsymbol{r}_{m}^{i})^{T}(\boldsymbol{r}_{m}- \boldsymbol{r}_{m}^{i})\\ & =\underbrace{-\frac{\delta_{m}}{2} \boldsymbol{r}_{m}^{T} \boldsymbol{r}_{m}+(\nabla\bar{g}(\boldsymbol{r}_{m}^{i})+ \delta_{m} \boldsymbol{r}_{m}^{i})^{T} \boldsymbol{r}_{m}}_{\tilde{g}(\boldsymbol{r}_{m})}+\\ &\qquad \underbrace{\bar{g}(\boldsymbol{r}_{m}^{i})-\frac{\delta_{m}}{2}(\boldsymbol{r}_{m}^{i})^{T} \boldsymbol{r}_{m}^{i}}_{\text{constant}}.\end{align*} gˉ(rm)≥gˉ(rmi)+∇gˉ(rmi)T(rm−rmi)−2δm(rm−rmi)T(rm−rmi)=g~(rm) −2δmrmTrm+(∇gˉ(rmi)+δmrmi)Trm+constant gˉ(rmi)−2δm(rmi)Trmi.(14)
因此,最大化 g ˉ ( r m ) \bar{g}(\boldsymbol{r}_{m}) gˉ(rm) 可以转换为最大化 g ~ ( r m ) ≜ δ m 2 r m T r m + ( ∇ g ˉ ( r m i ) + δ m r m i ) T r m \tilde{g}(\boldsymbol{r}_{m})\triangleq\frac{\delta_{m}}{2}\boldsymbol{r}_{m}^{T}\boldsymbol{r}_{m}+(\nabla\bar{g}(\boldsymbol{r}_{m}^{i})+\delta_{m}\boldsymbol{r}_{m}^{i})^{T}\boldsymbol{r}_{m} g~(rm)≜2δmrmTrm+(∇gˉ(rmi)+δmrmi)Trm。为此,在SCA的第i次迭代中,它们的MA位置 r m \boldsymbol{r}_{m} rm 的优化问题可以放松为
( P 4 − m ) max r m − δ m 2 r m r m + ( ∇ g ˉ ( r m i ) + δ m r m i ) T r m s . t . ( 12 b ) , ( 12 c ) . \begin{align*}(\mathrm{P}4-\mathrm{m}) & \max_{\boldsymbol{r}_{m}}\quad -\frac{\delta_{m}}{2}\boldsymbol{r}_{m}\boldsymbol{r}_{m}+(\nabla\bar{g}(\boldsymbol{r}_{m}^{i})+ \delta_{m}\boldsymbol{r}_{m}^{i})^{T}\boldsymbol{r}_{m}\tag{15}\\ & \mathrm{s}.\mathrm{t}.\quad (12\mathrm{b}), (12\mathrm{c}).\end{align*} (P4−m)rmmax−2δmrmrm+(∇gˉ(rmi)+δmrmi)Trms.t.(12b),(12c).(15)
由于 ∥ r m − r k ∥ 2 \Vert \boldsymbol{r}_{m}-\boldsymbol{r}_{k}\Vert_{2} ∥rm−rk∥2 是关于 r m \boldsymbol{r}_{m} rm 的凸函数,在给定的点边缘应用一阶泰勒展开,我们得到以下不等式:
∥ r m − r k ∥ 2 ≥ 1 ∥ r m i − r k ∥ 2 ( r m i − r k ) T ( r m − r k ) . \begin{equation*}\Vert \boldsymbol{r}_{m}-\boldsymbol{r}_{k}\Vert_{2}\geq\frac{1}{\Vert \boldsymbol{r}_{m}^{i}-\boldsymbol{r}_{k}\Vert_{2}}(\boldsymbol{r}_{m}^{i}-\boldsymbol{r}_{k})^{T}(\boldsymbol{r}_{m}-\boldsymbol{r}_{k}). \tag{17}\end{equation*} ∥rm−rk∥2≥∥rmi−rk∥21(rmi−rk)T(rm−rk).(17)
如果 r m , i + 1 ⋆ \boldsymbol{r}_{m,i+1}^{\star} rm,i+1⋆ 不满足(12b)或(12c),则第m个MA的凸位置优化问题转化为 ( P 5 − m ) max r m − δ m 2 r m T r m + ( ∇ g ˉ ( r m i ) + δ m r m i ) T r m s . t . 1 ∥ r m i − r k ∥ 2 ( r m i − r k ) T ( r m − r k ) ≥ D , k = 1 , 2 , … , M , k ≠ m , ( 12 b ) . \begin{align*}(P5-m) \max\limits_{\boldsymbol{r}_{m}} & -\frac{\delta_{m}}{2}\boldsymbol{r}_{m}^{T}\boldsymbol{r}_{m}+(\nabla\bar{g}(\boldsymbol{r}_{m}^{i})+ \delta_{m}\boldsymbol{r}_{m}^{i})^{T}\boldsymbol{r}_{m}\tag{18a}\\ & \mathrm{s}.\mathrm{t}. \frac{1}{\Vert \boldsymbol{r}_{m}^{i}-\boldsymbol{r}_{k} \Vert_{2}}(\boldsymbol{r}_{m}^{i}-\boldsymbol{r}_{k})^{T}(\boldsymbol{r}_{m}-\boldsymbol{r}_{k})\geq D,\\ & k=1,2, \ldots, M, k\neq m,\tag{18b}\\ & (12\mathrm{b}).\end{align*} (P5−m)rmmax−2δmrmTrm+(∇gˉ(rmi)+δmrmi)Trms.t.∥rmi−rk∥21(rmi−rk)T(rm−rk)≥D,k=1,2,…,M,k=m,(12b).(18a)(18b)
APPENDIX


关于A,就是单纯的代入公式,没有什么可以细讲的。B当中有一个小疑点,就是为何 ∥ ∇ 2 g ˉ ( r m ) ∥ 2 I 2 ⪰ ∇ 2 g ˉ ( r m ) \left\|\nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right)\right\|_{2} \boldsymbol{I}_{2} \succeq \nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right) ∇2gˉ(rm) 2I2⪰∇2gˉ(rm)。我来稍微解释一下, ∥ A ∥ 2 = λ max ( A ∗ A ) = σ max ( A ) \|A\|_{2}=\sqrt{\lambda_{\max }\left(A^{*} A\right)}=\sigma_{\max }(A) ∥A∥2=λmax(A∗A)=σmax(A),表示 A 最大的那个特征值,但是 ∥ A ∥ F = ∑ i m ∑ j n ∣ a i j ∣ 2 = trace ( A ∗ A ) = ∑ i = 1 min { m , n } σ i 2 ( A ) \|A\|_{\mathrm{F}}=\sqrt{\sum_{i}^{m} \sum_{j}^{n}\left|a_{i j}\right|^{2}}=\sqrt{\operatorname{trace}\left(A^{*} A\right)}=\sqrt{\sum_{i=1}^{\min \{m, n\}} \sigma_{i}^{2}(A)} ∥A∥F=i∑mj∑n∣aij∣2=trace(A∗A)=i=1∑min{m,n}σi2(A)因此很容易可以得到 ∥ ∇ 2 g ˉ ( r m ) ∥ 2 2 ≤ ∥ ∇ 2 g ˉ ( r m ) ∥ F 2 \left\|\nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right)\right\|_{2}^{2} \leq\left\|\nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right)\right\|_{F}^{2} ∇2gˉ(rm) 22≤ ∇2gˉ(rm) F2。很显然 ∥ ∇ 2 g ˉ ( r m ) ∥ 2 I 2 − ∇ 2 g ˉ ( r m ) \left\|\nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right)\right\|_{2} \boldsymbol{I}_{2} - \nabla^{2} \bar{g}\left(\boldsymbol{r}_{m}\right) ∇2gˉ(rm) 2I2−∇2gˉ(rm) 是对称矩阵,因为 A symmetric matrix is psd(positive semi-definite) if and only if all eigenvalues are non-negative,详细的证明可以参见网站1,网站2,网站3。下面的截图,给出了证明的主要思路。


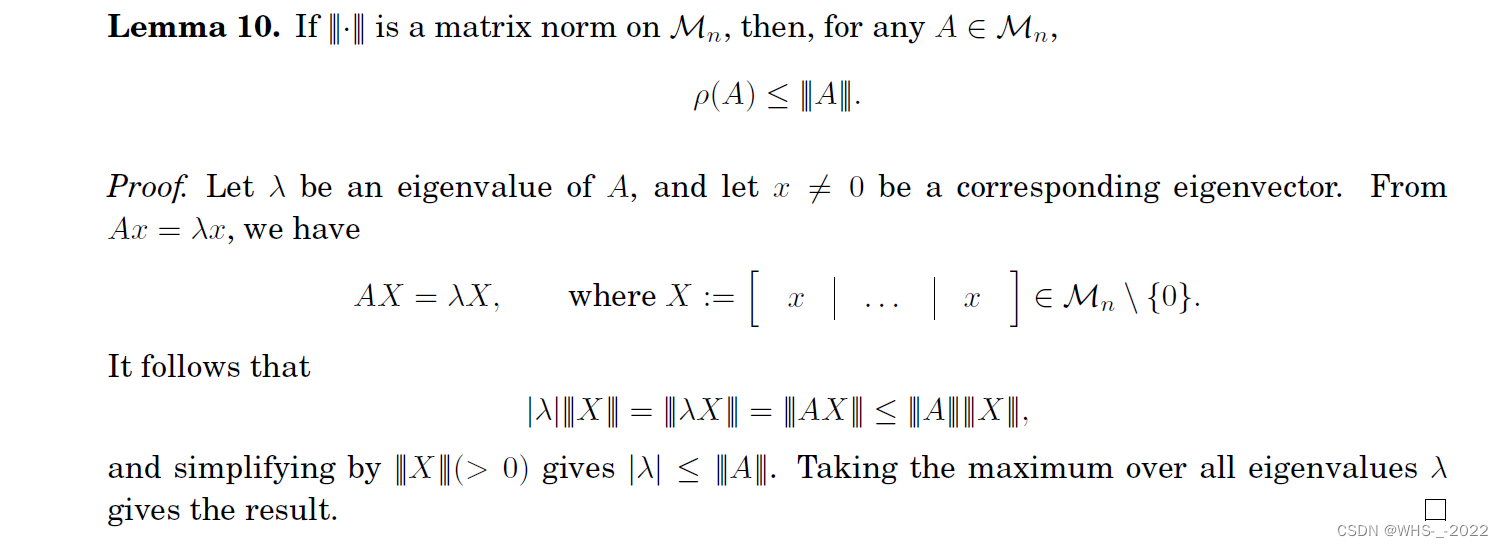





-Linux ARM驱动编程第三天-ARM Linux ADC和触摸屏开发 (物联技术666))




)





)





