目录结构
注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下:
1、参考书籍:《算法导论》第三版 就是这本被封神的杰作,就是它🤦
2、参考书籍:《数据结构》严奶奶版
3、参考书籍:《数据结构》(用面向对象方法与C++语言描述) 第二版 殷人昆版
4、参考书籍:《数据结构》(C++版) 第三版 邓俊辉版
5、华中科技大学 有向无环图及应用 公开课,点击前往
6、OI Wiki 有向无环图,点击前往
7、OI Wiki 拓扑排序,点击前往
8、关键路径 + 拓扑排序,点击前往
DSA 经典数据结构与算法 有向无环图
- 文章快速说明索引
- 有向无环图的背景
- 拓扑排序
- 逆拓扑排序
- AOV 网
- 关键路径和 AOE 网

文章快速说明索引
学习目标:
前言:还记得在大学的时候,数据结构作为计算机科学与技术专业最重要的一门课 当时学校采用的教材是严奶奶的粉红色那本,不过当时是真的不愿多看一眼 😂 苦涩难懂 又非常深奥,满篇伪代码实现的例子和夏日那十分惬意的下午 简直让人头大而晕!
也可能是上学那会儿年少浮躁,也可能是因为当时的能力比较的菜吧 ┑( ̄Д  ̄)┍ 。现在再回头捧读厚厚的《算法导论》,竟然有一种说不上来的快乐 沉浸在数据结构和算法之美,惊叹于高超技巧式拍案惊奇!
学习内容:(详见目录)
1、数据结构与算法(DSA)之有向无环图
学习时间:
2024年02月15日 14:17:05
学习产出:
1、CSDN 技术博客 1篇
有向无环图的背景
有向无环图(Directed Acyclic Graph):一个无环的有向图。
- 其性质如下:
- 能 拓扑排序 的图,一定是有向无环图;如果有环,那么环上的任意两个节点在任意序列中都不满足条件了
- 有向无环图,一定能拓扑排序;(归纳法)假设节点数不超过 k 的 有向无环图都能拓扑排序,那么对于节点数等于 k 的,考虑执行拓扑排序第一步之后的情形即可
- 如何判定一个图是否是有向无环图呢?
- 检验它是否可以进行 拓扑排序 即可
- 当然也有另外的方法,可以对图进行一遍 DFS,在得到的 DFS 树上看看有没有连向祖先的非树边(返祖边)。如果有的话,那就有环了
接下来看一下 DAG 的应用, 如下:
一、描述表达式:
// 如下表达式含 + * 操作((a + b) * (b * (c + d)) + (c + d) * e) * ((c + d) * e)
用二叉树表示这个表达式,(21个顶点)如下:
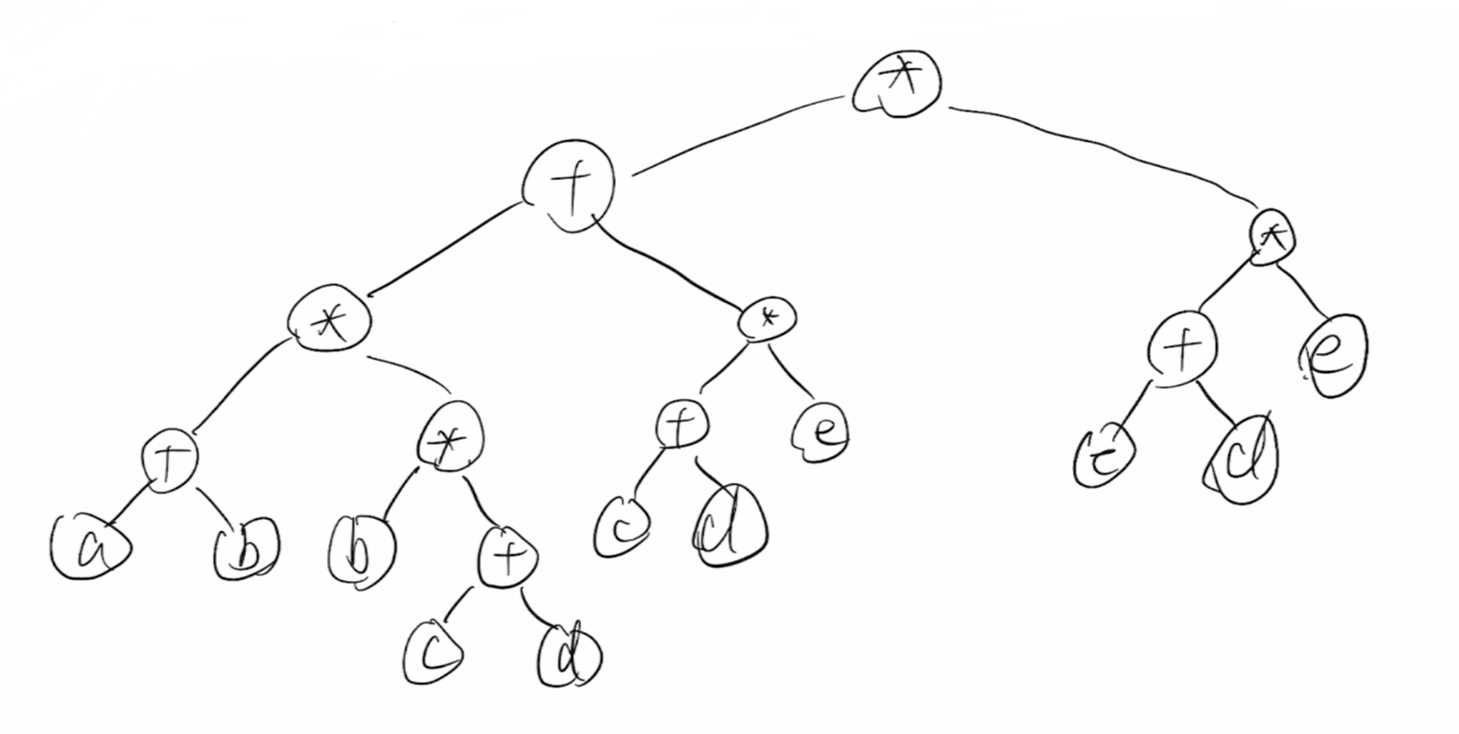
用有向无环图表示该表达式,(12个顶点)如下:
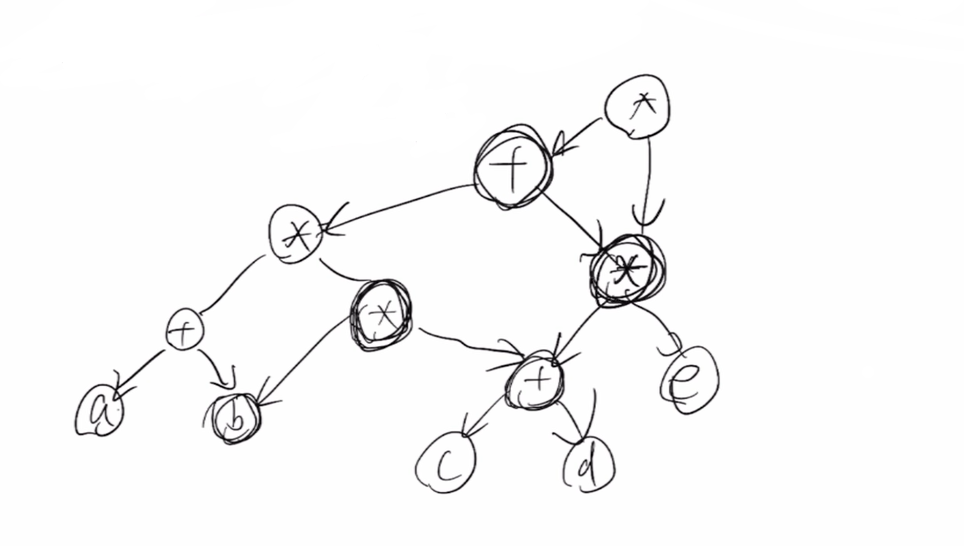
二、表示 AOV网 (Activity On Vertex Network) or AOE网(Activity On Edge)

- 什么是AOV网与AOE网?——以及AOV网与AOE网区别和运用,点击前往
下面我们再详细介绍它们!
拓扑排序
拓扑排序的英文名是 Topological sorting。拓扑排序要解决的问题是给一个有向无环图的所有节点排序。换言之:其是一个有向无环图(DAG,Directed Acyclic Graph)的所有顶点的线性序列,且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面
- 有向无环图(DAG)才有拓扑排序,非DAG就没有拓扑排序一说
一个经典的案例,如下:
因此我们可以说:
- 在一个 DAG(有向无环图) 中,我们将图中的顶点以线性方式进行排序,使得对于任何的顶点 u 到 v 的有向边 (u,v),都可以有 u 在 v 的前面
- 还有给定一个 DAG,如果从 i 到 j 有边,则认为 j 依赖于 i。如果 i 到 j 有路径(i 可达 j),则称 j 间接依赖于 i
- 拓扑排序的目标是将所有节点排序,使得排在前面的节点不能依赖于排在后面的节点
举一个例子,如下:
- 拓扑排序(Topological Sorting),点击前往
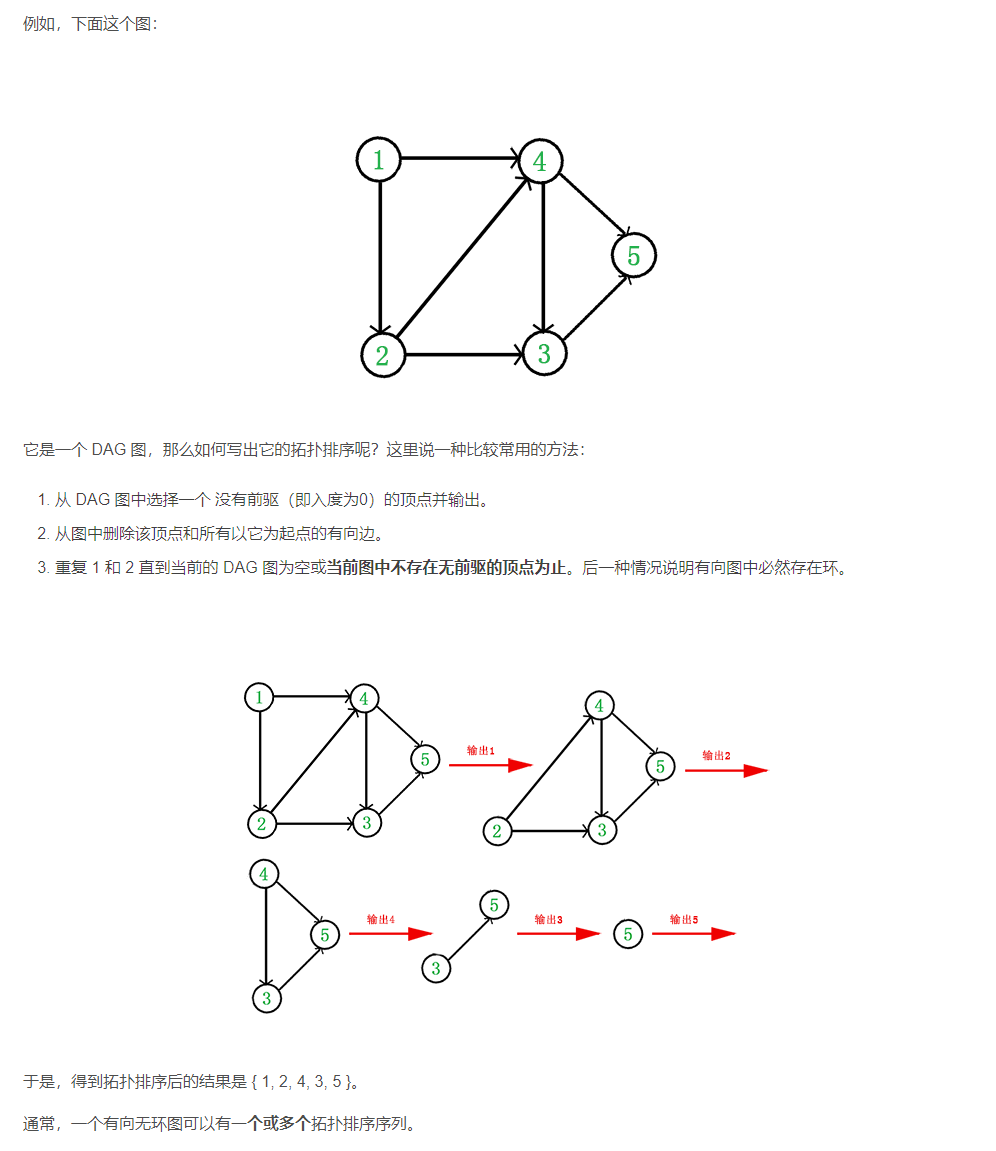
逆拓扑排序
逆拓扑排序的步骤:
- 从AOV网中选择一个出度为0的顶点并输出
- 从网中删除该顶点和所有以它为终点的有向边
- 重复1和2,直到当前的AOV网为空
AOV 网
日常生活中,一项大的工程可以看作是由若干个子工程组成的集合,这些子工程之间必定存在一定的先后顺序,即某些子工程必须在其他的一些子工程完成后才能开始。
我们用有向图来表现子工程之间的先后关系,子工程之间的先后关系为有向边,这种有向图称为顶点活动网络,即 AOV 网 (Activity On Vertex Network)。一个 AOV 网必定是一个有向无环图,即不带有回路。与 DAG 不同的是,AOV 的活动都表示在边上。
在 AOV 网中,顶点表示活动,弧表示活动间的优先关系。AOV 网中不应该出现环,这样就能够找到一个顶点序列,使得每个顶点代表的活动的前驱活动都排在该顶点的前面,这样的序列称为拓扑序列(一个 AOV 网的拓扑序列不是唯一的),由 AOV 网构造拓扑序列的过程称为拓扑排序。因此,拓扑排序也可以解释为将 AOV 网中所有活动排成一个序列,使得每个活动的前驱活动都排在该活动的前面(一个 AOV 网中的拓扑排序也不是唯一的)。
- 前驱活动:有向边起点的活动称为终点的前驱活动(只有当一个活动的前驱全部都完成后,这个活动才能进行)
- 后继活动:有向边终点的活动称为起点的后继活动
检测 AOV 网中是否带环的方式是构造拓扑序列,看是否包含所有顶点。构造这个拓扑序列步骤:
- 从图中选择一个入度为零的点
- 输出该顶点,从图中删除此顶点及其所有的出边
- 重复上面两步,直到所有顶点都输出,拓扑排序完成,或者图中不存在入度为零的点,此时说明图是有环图,拓扑排序无法完成,陷入死锁
关键路径和 AOE 网
与 AOV 网对应的是 AOE 网(Activity On Edge Network) 即边表示活动的网。AOE 网是一个带权的有向无环图,其中,顶点表示事件,弧表示活动持续的时间。通常,AOE 网可以用来估算工程的完成时间。AOE 网应该是无环的,且存在唯一入度为零的起始顶点(源点),以及唯一出度为零的完成顶点(汇点)。
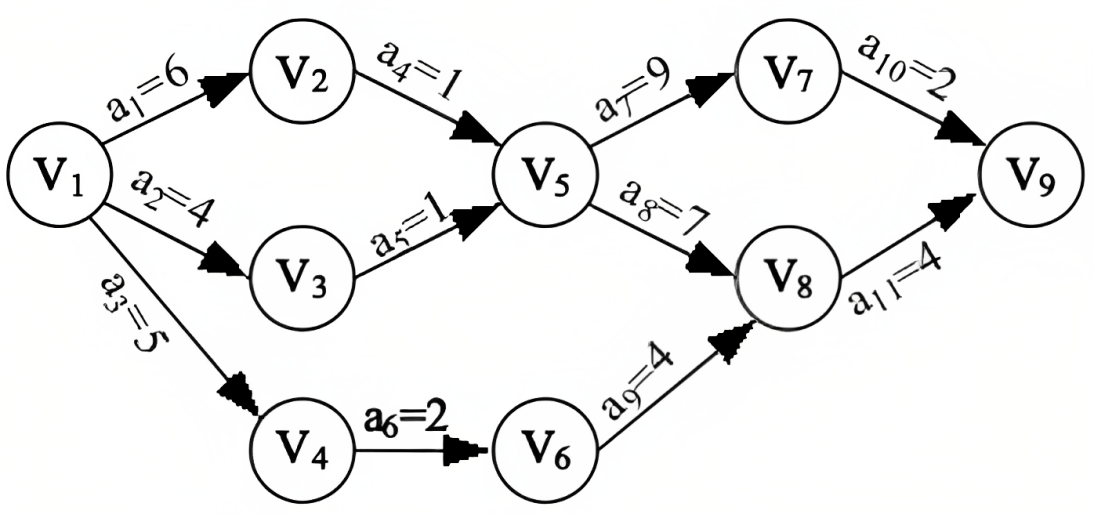
AOE 网中的有些活动是可以并行进行的,所以完成整个工程的最短时间是从开始点到完成点的最长活动路径长度(这里所说的路径长度是指路径上各活动的持续时间之和,即弧的权值之和,不是路径上弧的数目)。因为一项工程需要完成所有工程内的活动,所以最长的活动路径也是关键路径,它决定工程完成的总时间。
AOE 网的相关基本概念,如下:
- 活动:AOE 网中,弧表示活动。弧的权值表示活动持续的时间,活动在事件被触发后开始。
- 事件:AOE 网中,顶点表示事件,事件能被触发。
- 弧(活动)aj 的最早开始时间:初始点到该弧起点的最长路径长度,记为 e(j)。
- 弧(活动)aj 的最迟开始时间:在不推迟整个工期的前提下,工程达到弧起点所表示的状态最晚能容忍的时间,记为 l(j)。即:事件的最迟发生时间 - 弧的活动时间值。
- 顶点(事件)vj 的最早发生时间:初始点到该顶点的最长路径长度,记为 ve(j),它决定了以该顶点开始的活动的最早发生时间,所以 ve(j) = e(j)。
- 顶点(事件)vj 的最迟发生时间:在不推迟整个工期的前提下,工程达到顶点所表示的状态最晚能容忍的时间,记为 vl(j),它决定了所有以该状态结束的活动的最迟发生时间,所以 l(j) = vl(j) - dul(aj)。
- 关键路径:AOE 网中从源点到汇点的最长路径的长度。
- 关键活动:关键路径上的活动,最早开始时间和最迟开始时间相等(看下面时间余量d(j) = 0的)。
最早和最迟发生时间的递推关系:
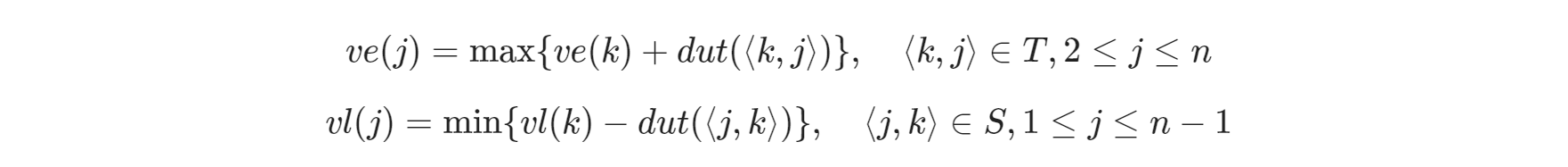
按拓扑顺序求,最早是从前往后,前驱顶点的最早开始时间与边的权重之和最大者;最迟是从后往前,后继顶点的最迟开始时间与边的权重之差的最小者。
下面看一个例子,计算如下:
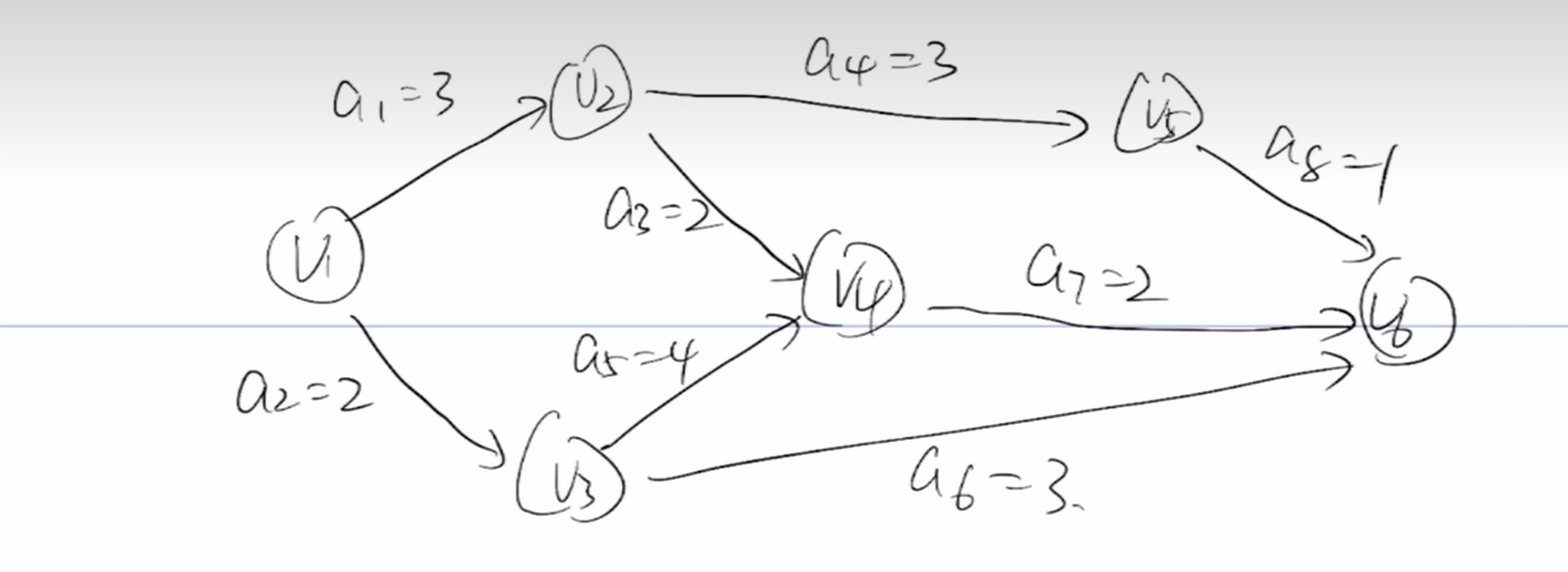
如上图,其其中之一的拓扑排序,如下:
V1 V3 V2 V5 V4 V6
| V1 | V2 | V3 | V4 | V5 | V6 | |
|---|---|---|---|---|---|---|
| ve(j):事件 的最早发生时间 -> | 0 | 3 | 2 | 6 max | 6 | 8 max |
| vl(j):事件 的最迟发生时间 <- | 0 | 4 min | 2 min | 6 | 7 | 8 |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | |
|---|---|---|---|---|---|---|---|---|
| e(j):活动 aj 的最早开始时间 -> | 0 | 0 | 3 | 3 | 2 | 2 | 6 | 6 |
| l(j):活动 aj 的最迟开始时间 <- | 4 - 3 | 2 - 2 | 6 - 2 | 7 - 3 | 6 - 4 | 8 - 3 | 8 - 2 | 8 - 1 |
| l(j):活动 aj 的最迟开始时间 <- | 1 | 0 | 4 | 4 | 2 | 5 | 6 | 7 |
| d(j):活动 aj 的时间余量 l(j) - e(j) | 1 | 0 | 1 | 1 | 0 | 3 | 0 | 1 |
于是关键活动有:a2 a5 a7。如下:
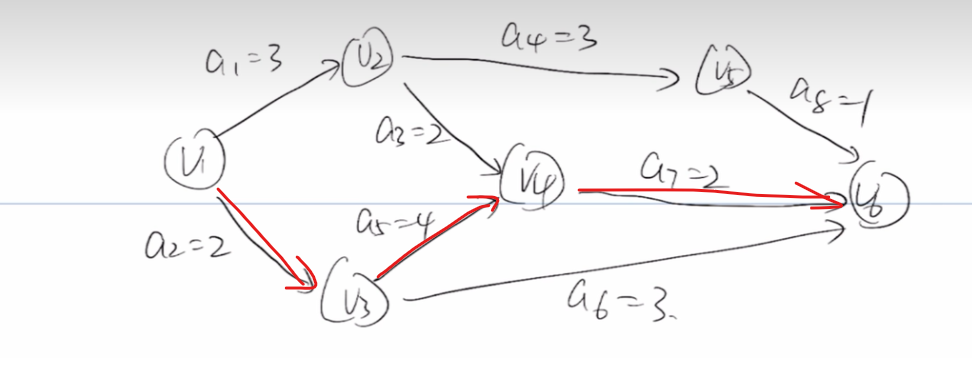
V1->V3->V4->V6 就是关键路径,total = 8!
关键路径算法:
- 输入 e 条弧 (j,k),建立 AOE 网;
- 从源点 v0 出发,令 ve[0] = 0, 按照拓扑排序求其余各个顶点的最早发生时间 ve[i], (i <= i <= n-1)。如果得到的拓扑有序序列中顶点的个数小于网中的顶点数 n,则说明网中存在环,不能求关键路径,算法终止;否则执行步骤 3;
- 从汇点 vn 出发,令 vl[n-1] = ve[n-1],按照逆拓扑有序求其余各顶点的最迟发生时间 vl[i], (n-2 >= i >= 2);
- 根据各顶点的 ve 和 vl 值,求每条弧 s 的最早开始时间 e(s) 和最迟开始时间 l(s)。若某条弧满足条件 e(s) = l(s), 则为关键活动。






 马尔可夫过程)

)






高级篇)


——计算机网络)
