树形dp 笔记

树的最长路径

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。

注意：路径中可以只包含一个点。

输入格式

第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出格式

输出一个整数，表示树的最长路径的长度。

数据范围

1≤n≤10000,
1≤ai,bi≤n,
−1e5≤ci≤1e5

输入样例：

输出样例：

边权不为负可以用两次dfs，边权有负就要用这种了

一个点选两个能走得贡献最大的孩子，相加就是能搭在这个点上最长的直径，所有点跑一遍，找最长的那个就行

理论上一个直径上每个点算出来的值都不一样，因为dfs得有个顺序，都是父亲向孩子走得，但每条直径都一定会被算到。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 20010;int pos, n;
int h[N], e[N], w[N], ne[N], idx;
int ans;void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}int dfs(int u, int father)
{int dist = 0;int d1 = 0, d2 = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dfs(j, u) + w[i];dist = max(dist, d);if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}ans = max(ans, d1 + d2);return dist;
}int main()
{IOScin >> n;memset(h, -1, sizeof h);for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);}dfs(1, -1);cout << ans;return 0;
}

树的中心

给定一棵树，树中包含 n个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入格式

第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出格式

输出一个整数，表示所求点到树中其他结点的最远距离。

数据范围

1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤1e5

输入样例：

输出样例：

可以延续上一题的思路，尝试枚举一下每个点

最远距离除了往下走的还有一条往上走的，要在两者中取一个最大值

dist数组存往下走的最大值，up数组存往上走的最大值

第一次dfs可以求出dist数组的每个值

然后第二次dfs可以用dist数组的值退出来up的值，根节点up为0，然后就可以按dfs顺序递推出来孩子的up的值了。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 20010;int pos, n;
int h[N], e[N], w[N], ne[N], idx;
int dist[N], up[N];
int ans = 2e9;void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}int dfs(int u, int father)
{int res = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dfs(j, u) + w[i];res = max(res, d);}dist[u] = res;return res;
}void dfs1(int u, int father)
{int d1 = 0, d2 = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int d = dist[j] + w[i];if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}if(up[u] > d1)d2 = d1, d1 = up[u];else if(up[u] > d2)d2 = up[u];for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(j == father)continue;int res;if(dist[j] + w[i] == d1)res = d2;else res = d1;up[j] = res + w[i];int tmp = max(up[j], dist[j]);ans = min(ans, tmp);dfs1(j, u);}
}int main()
{IOScin >> n;memset(h, -1, sizeof h);for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);}dfs(1, -1);dfs1(1, -1);ans = min(ans, dist[1]);cout << ans;return 0;
}

数字转换

如果一个数 x 的约数之和 y（不包括他本身）比他本身小，那么 x 可以变成 y，y 也可以变成 x。

例如，4 可以变为 3，1 可以变为 7。

限定所有数字变换在不超过 n 的正整数范围内进行，求不断进行数字变换且不出现重复数字的最多变换步数。

输入格式

输入一个正整数 n。

输出格式

输出不断进行数字变换且不出现重复数字的最多变换步数。

数据范围

1≤n≤50000

输入样例：

输出样例：

样例解释

一种方案为：4→3→1→7。

可以把每个数字看成一个点，求得问题转换为求树的直径

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 50010;int n;
vector<int> g[N];
int ans;
bool st[N];
int sum[N];int get(int x)
{int res = 1;for(int i = 2; i * i <= x; i ++){if(x % i == 0){res += i;if(x / i != i)res += x / i;}}return res;
}int dfs(int u, int father)
{int d1 = 0, d2 = 0;for(auto j : g[u]){if(j == father)continue;int d = dfs(j, u) + 1;if(d > d1)d2 = d1, d1 = d;else if(d > d2)d2 = d;}ans = max(ans, d1 + d2);return d1;
}int main()
{IOScin >> n;for (int i = 1; i <= n; i ++)for (int j = 2; j <= n / i; j ++)sum[i * j] += i;for (int i = 2; i <= n; i ++)if (sum[i] < i){g[sum[i]].push_back(i);g[i].push_back(sum[i]);}dfs(1, -1);cout << ans;return 0;
}

二叉苹果树

有一棵二叉苹果树，如果树枝有分叉，一定是分两叉，即没有只有一个儿子的节点。

这棵树共 N 个节点，编号为 1 至 N，树根编号一定为 1。

我们用一根树枝两端连接的节点编号描述一根树枝的位置。

一棵苹果树的树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

这里的保留是指最终与1号点连通。

输入格式

第一行包含两个整数 N 和 Q，分别表示树的节点数以及要保留的树枝数量。

接下来 N−1 行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。

输出格式

输出仅一行，表示最多能留住的苹果的数量。

数据范围

1≤Q<N≤100.
N≠1,
每根树枝上苹果不超过 30000个。

输入样例：

输出样例：

有依赖的背包问题的简化版

f[u][j]表示节点u，可分配树枝数量为j，最大值（j也可理解为背包容量，但也有点不一样，这个容量不包括本身在内）

理解写在注释里了

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 110, M = 210;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[N][N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void dfs(int u, int father)
{for(int i = h[u]; i != -1; i = ne[i])//第i个物品组{//int j = e[i];if(e[i] == father)continue;dfs(e[i], u);for(int j = m; j >= 0; j --)//背包容量{for(int k = 0; k < j; k ++)//不同决策{f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);//分组背包是物品组里的每个物品体积和价值不同//            f[u][i-1][j]    f[u][i-1][j-vk] + w}}}
}int main()
{IOSmemset(h, -1, sizeof h);cin >> n >> m;for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}dfs(1, -1);cout << f[1][m];return 0;
}

战略游戏

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

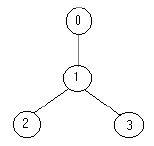
1463_1.jpg.gif

只需要放置 1 名士兵（在节点 1 处），就可观察到所有的边。

输入格式

输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数 N，表示树的节点数目。

接下来 N 行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点子节点 …

节点编号从 0 到 N−1，每个节点的子节点数量均不超过 10，每个边在输入数据中只出现一次。

输出格式

对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围

0<N≤1500,
一个测试点所有 N 相加之和不超过 300650。

输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 1510;int n;
vector<int> g[N];
int d[N];
int f[N][2];void dfs(int u)
{f[u][0] = 0;f[u][1] = 1;for(auto j : g[u]){dfs(j);f[u][0] += f[j][1];f[u][1] += min(f[j][0], f[j][1]);}
}int main()
{IOSwhile(cin >> n){for(int i = 0; i <= n; i ++){g[i].clear();d[i] = 0;f[i][0] = f[i][1] = 0;}int ver1, ver2, num;char tmp;for(int i = 0; i < n; i ++){cin >> ver1 >>tmp >> tmp >> num >> tmp;for(int i = 0; i < num; i ++){cin >> ver2;g[ver1].push_back(ver2);d[ver2] ++;}}int root;for(int i = 0; i < n; i ++){if(!d[i]){root = i;break;}}dfs(root);cout << min(f[root][0], f[root][1]) << endl;}return 0;
}

皇宫看守

太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。

皇宫各个宫殿的分布，呈一棵树的形状，宫殿可视为树中结点，两个宫殿之间如果存在道路直接相连，则该道路视为树中的一条边。

已知，在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况，还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。

大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。

可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

输入格式

输入中数据描述一棵树，描述如下：

第一行 n，表示树中结点的数目。

第二行至第 n+1 行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号 i，在该宫殿安置侍卫所需的经费 k，该结点的子结点数 m，接下来 m 个数，分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。

对于一个 n 个结点的树，结点标号在 1 到 n 之间，且标号不重复。

输出格式

输出一个整数，表示最少的经费。

数据范围

1≤n≤1500

输入样例：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例：

样例解释：

在2、3、4结点安排护卫，可以观察到全部宫殿，所需经费最少，为 16 + 5 + 4 = 25。

本来以为和上一题差不多结果wa了

发现有一种情况是上一题没有的：

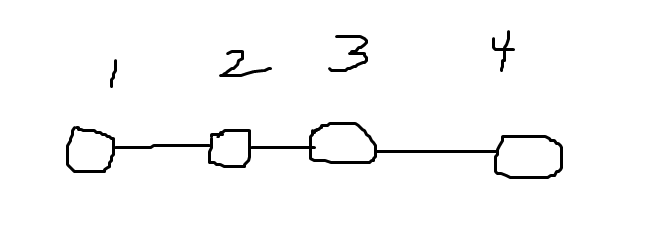
选1、4点也是符合要求的

f[u][0] 不放，但能被父节点看到
f[u][1] 不放，但能被子节点看到
f[u][2] 放

f[u][0]和f[u][2]都很好像，主要是如何得到f[u][1]，能被子节点看到，那就选能被哪个子节点看到，其他点取min(f[u][1], f[u][2]),在所有方案中选个最小值

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 1510;int n;
vector<int> g[N];
int w[N], d[N];
int f[N][3];
//f[u][0] 不放，但能被父节点看到
//f[u][1] 不放，但能被子节点看到
//f[u][2] 放 void dfs(int u)
{f[u][0] = 0, f[u][1] = 0, f[u][2] = w[u];int sum = 0;for(auto j : g[u]){dfs(j);f[u][0] += min(f[j][1], f[j][2]);sum += min(f[j][1], f[j][2]);f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);}int res = 2e9;for(auto j : g[u]){res = min(res, sum + f[j][2] - min(f[j][1], f[j][2]));}f[u][1] = res;
}int main()
{IOScin >> n;for(int i = 0; i < n; i ++){int id, val, num;cin >> id >> val >> num;w[id] = val;for(int j = 0; j < num; j ++){int x;cin >> x;d[x] ++;g[id].push_back(x);}}int root;for(int i = 1; i <= n; i ++){if(!d[i]){root = i;break;}}dfs(root);cout << min(f[root][1], f[root][2]);return 0;
}