情有独钟的素数

什么是素数

素数（Prime number）也称为质数，是指在非0自然数中，除了1与其本身之外不拥有其他因数的自然数。也就是说，素数需要满足两个条件：

• 大于1的整数；
• 只拥有1和其自身两个因数。

例子1

本文章的任务就是输出100以内的所有素数，如2、3、5、7、11、13…
先理清一下思路：
（1）需要有一个2~100的外循环，还要有一个小于当前数的因子内循环；
（2）需要有一个判断是否可整除的i语句（整除就是余数为0）。
求100以内的素数的思路如下图所示。

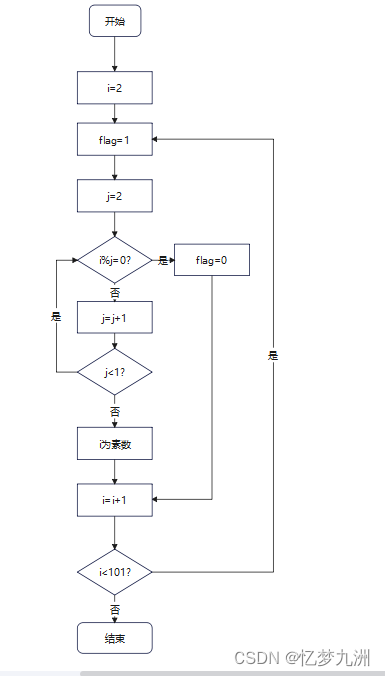
代码实现

实现代码如下：
Python

# 100以内的素数算法
prime = []
#从2开始遍厉到100
for i in range (2,101) :flag =1 #i是否力素数的标记# 因数应该是大于1小于自身的数for j in range (2, i):if i%j ==0: #一旦取模（余数）为0flag = 0 # 更改标记为0break   # 直接跳出本循环if flag == 1: # 标记为 1，则为素数prime.append(i) # 添加到 prime 列表
print("100以内的素数：",prime)

Java

 List<Integer> arr = new ArrayList<>();int flag ;for(int i=2;i<101;i++){flag =1;for (int j=2;j<i;j++){if(i%j==0){flag =0;break;}}if(flag==1){arr.add(i);}}System.out.println(arr);

输出结果如下：

例子2 “优化素数计算：从暴力求解到开方优化”

只要解决了问题就结束了吗？这可不是学习的态度。《诗经》有云：“如切如磋，如琢如磨。”其斯之谓与？我们可要精益求精啊。这段代码虽实现了我们的任务，但它的时间复杂度太大，100 以内的素数还可以，如果是1000或10000呢？
可是要怎样使时间复杂度变小呢？只有两个地方可以下手——要么是外循环，要么是内循环。我们知道：任意数若等于两个非0自然数的乘积，则这两个因子中至少有一个小于该数的二分之一。
当然，我们还可以再缩小一下范围，把“二分之一”缩减为“开方”，这样就大大缩减了内循环的运行时间。思路如下图所示。

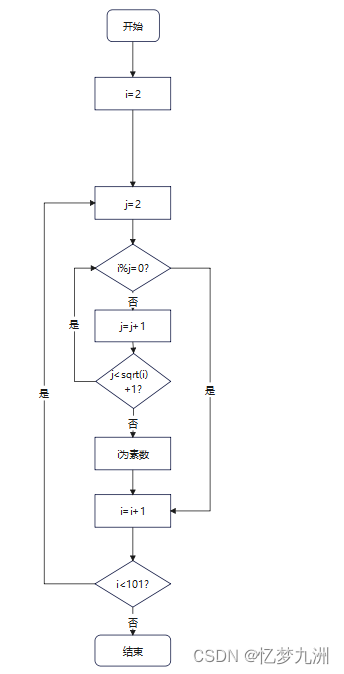
代码实现

实现代码如下：
Python

# -*- coding: utf-8 -*-
import math#100以内的素数算法二
prime = []
#从2开始遍历到 100
for i in range (2,101) :#因数应该是大于1小于自身的开方+1for j in range(2,int(math.sqrt(i))+1):#一旦取模（余数）为0if i%j == 0:break   #直接跳出本循环# 若余数均不0，则为素数else:prime.append(i) # 添加到 prime 列表中print("100以内的全部素数：",prime)

Java

 	List<Integer> arr = new ArrayList<>();int j;for(int i=2;i<101;i++){for (j=2;j<(int)Math.sqrt(i)+1;j++){if(i%j==0){break;}}if(j==(int)Math.sqrt(i)+1){arr.add(i);}}System.out.println(arr);

注意：例子二的内循环范围记得加1，否则输出结果错误

输出结果如下：

看，我们只改了一个值，便大大缩短了算法的运行时间，这就是思维逻辑的重要性。只要逻辑捋顺了，代码实现就很容易了。

例子3

观察结果发现，5+1=6，7-1=6，11+1=12,13-1=12, 17+1=18，19-1=18,23+1=24…这些都是6的倍数，那我们当不是可以利用（6n-1）和（6n+1）两个公式便可以得到质数的排列了？那么下一个质数必该是6×4+1=35，再下个质数就是6×5-1=29，但是25并不是质数，因此排列的规律还需要我们一步步地分析。
我们先不看2和3，从5开始往后数，所有的素数都分布在6n（n≥1）左右两侧，即（6n-1）与（6n+1）。那以6为间距的其他数又是如何分布的呢？6n %6=0，（6n+2）%2=0，（6n+3）%3=0，（6n+4）%2=0，（6n+5）则又回到了（6n-1），一个循环结束了。
我们发现：除去2和3以外，所有的素数都是符合（6n-1）和（6n+1）规律的，但符合这两个公式的数字不一定就是素数，因此这是一个充分非必要条件，而不是充要条件。
据此，我们可以进一步缩小因子范围，思路如下图所示。

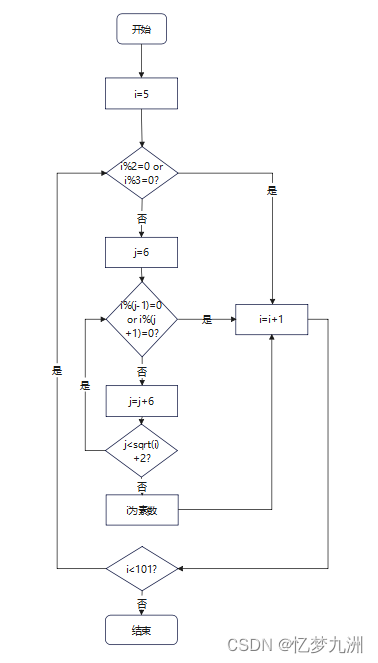
代码实现

实现代码如下：
Python

# -*- coding: utf-8 -*-
import math# 100 以内的素数算法三
prime = []
prime. extend([2, 3]) #已知2和3 是素数
# 从5开始遍历到 100
for i in range (5,101) :# 非素数时if i % 2 == 0 or i%3 ==0 :continue # 跳过后续操作，直接进入下一循环# 因数应该是大于1小于自身的开方+2，以6为单位for j in range(6, int(math.sqrt(i))+2,6):# 当可以整除6 的倍数时两侧的数字也为非素数if i%(j-1) == 0 or i%(j+1) ==0:break # 直接跳出本循环# 若余数均不为O，则为素数else:prime.append(i)
# 添加到 prime 列表中
print("100以内的全部素数：",prime)

Java

List<Integer> arr = new ArrayList<>();arr.add(2);arr.add(3);int j;for(int i=5;i<101;i++){if (i%2==0 || i%3==0)continue;for (j=6;j<(int)Math.sqrt(i)+2;j+=6){if(i%(j-1)==0 || i%(j+1)==0){break;}}if(j>=(int)Math.sqrt(i)+2){arr.add(i);}}System.out.println(arr);

注意：continue 和 break 非常好用，不熟悉它们的用法的读者请务必掌握。

输出结果如下：

“素数的广泛应用与未解决的数学难题”

这么一看果然“顺眼”多了，虽然思路让人不好理解，但多看几遍还是能理解的。一般来说，实现相同功能的不同代码，越简洁的就越晦涩，运行时间越少的也越难懂。当然，素数的检测算法远不止于此，还有费马素性测试（Fermat primality test）、米勒-拉宾素性测试 （Miller-Rabin primality test）、Solovay-Strassen 测试、卢卡斯-菜默素性测试 （Lucas-Lehmer primality test）和埃拉托斯特尼筛法等。素数在自然数中的分布极其复架，其被广泛应用到密码学中，即在公钥中插入素数并进行编码，以此达到提高破译难度的目的。
同时，素数领域还存在许多数学家们一直无法解决的难题，最著名的莫过于“哥德巴赫猜想”和“黎曼猜想”。哥德巴赫和黎曼在数学界都是举足轻重的人物。哥德巴赫猜想是：“是否每个大于2的偶数都可写成两个素数之和？”娶曼猜想是：“素数出现的频率与黎曼$\zeta$函数紧密相关。”这两个猜想虽然未能被完全验证，但已经被广泛应用，黎曼猜想甚至已经成为当今数学文献中一千多条数学命题的前提。