🎇个人主页：Ice_Sugar_7
🎇所属专栏：Java数据结构
🎇欢迎点赞收藏加关注哦！

🍉概念

Map和Set是专门用来进行搜索的容器或者数据结构，它们适合动态查找（即在查找时可能会进行一些插入和删除的操作）

🍉模型

我们一般把搜索的数据称为关键字（Key），和关键字对应的称为值（Value），将其称之为Key-Value的键值对，所以有两种模型：

1. 纯 Key 模型，比如：
   有一个英文词典，快速查找一个单词是否在词典中
   快速查找某个名字在不在通讯录中

2. Key-Value 模型，比如：
   统计文件中每个单词出现的次数，统计结果是每个单词都有与其对应的次数：<单词，单词出现的次数>

Map中存储的是Key-Value的键值对，Set中只存储了Key

🍉Map

Map是一个接口类，该类没有继承自Collection
该类中存储<K,V>结构的键值对，并且K一定是唯一的，不能重复

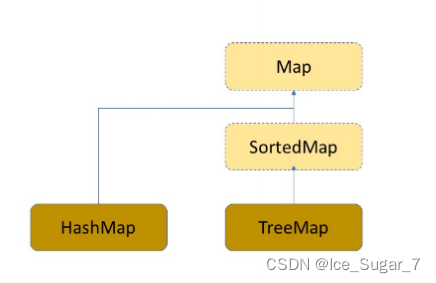
注意：

• Map是一个接口，不能直接实例化对象，如果要实例化对象，只能实例化其实现类TreeMap或HashMap
• Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉
• Map中存放键值对的key是唯一的，而value是可以重复的。如果向Map中添加一个已经存在的键，那么新的value会覆盖原有的value
• 在TreeMap中插入键值对时，key不能为空，否则会抛NullPointerException异常，value可以为空。但是HashMap的key和value都可以为空

🍌TreeMap和HashMap的区别

区别	TreeMap	HashMap
底层结构	红黑树	哈希桶
元素顺序	元素按Key的自然顺序或自定义的比较器进行排序	无序，因为哈希表的存储和遍历是无序的
查找、插入和删除操作的时间复杂度	O(log n)	O（1）
比较和重写	key必须能够比较	自定义类型需要重写equals和hashCode方法
应用场景	需要Key有序的场景下	不关心Key是否有序，需要更高的时间性能

---

🍌Map常用方法

方法	功能
V get(Object key)	返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)	返回 key 对应的 value，key 不存在，返回默认值
V put(K key, V value)	设置 key 对应的 value
V remove(Object key)	删除 key 对应的映射关系
Set< K > keySet()	返回所有 key 的不重复集合
Collection< V > values()	返回所有 value 的可重复集合
Set<Map.Entry<K, V>> entrySet()	返回所有的 key-value 映射关系
boolean containsKey(Object key)	判断是否包含 key
boolean containsValue(Object value)	判断是否包含 value

🍌entrySet和keySet方法

上面的entrySet()方法返回Set<Map.Entry<K, V>>。其中的Map.Entry<K,V>是Map内部的一个接口，表示Map中的键值映射关系，可以将它类比为链表中的节点
这个接口主要提供了<Key, Value>的获取，value的设置以及key的比较方式

方法	功能
K getKey()	返回Entry中的key
V getValue()	返回Entry中的value
V setValue(V value)	将键值对中的value替换为指定value

要获取Map的key和value，我们需要借助entrySet方法，来道题演示一下：
只出现一次的数字II

思路：使用哈希表统计数组中每个元素的出现次数，Key为元素的值，Value为出现次数

class Solution {public int singleNumber(int[] nums) {Map<Integer,Integer> map = new HashMap<>();for(int num : nums) {map.put(num, map.getOrDefault(num,0)+1);}for(Map.Entry<Integer,Integer> entry: map.entrySet()) {if(entry.getValue() == 1) {return entry.getKey();}}return -1;}
}

keySet方法也可以拿到Map中的key，再通过get方法就可以拿到对应的value：

Map<String, Integer> map = new HashMap<>();
// 添加键值对
map.put("A", 1);
map.put("B", 2);
map.put("C", 3);// 遍历key集合
for (String key : map.keySet()) {Integer value = map.get(key); // 通过key获取valueSystem.out.println("Key: " + key + ", Value: " + value);
}

---

🍉Set

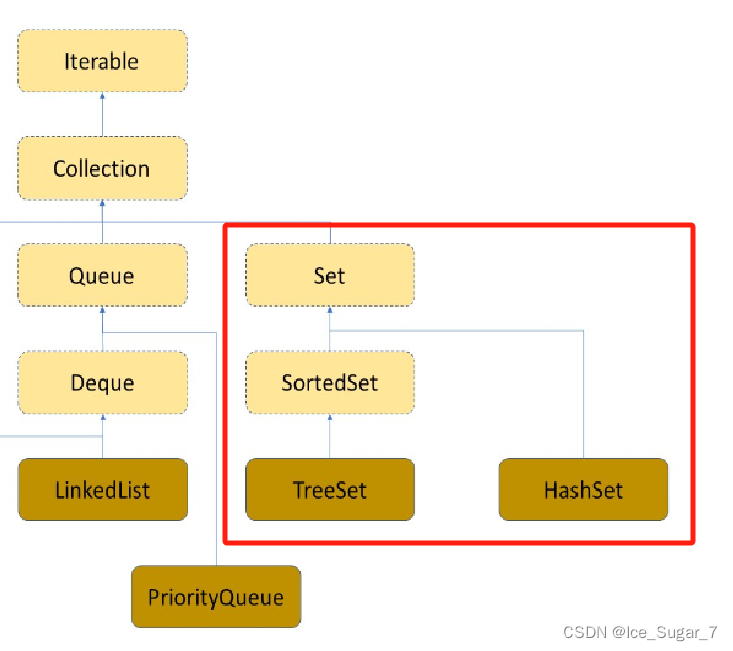
Set与Map主要有两点不同：

1. Set是继承自Collection的接口类
2. Set中只存储了Key

🍌Set常用方法

方法	功能
boolean add(E e)	添加元素，如果Set中已经有这个元素，则不会被添加
void clear()	清空集合
boolean contains(Object o)	判断 o 是否在集合中
Iterator< E > iterator()	返回迭代器
boolean remove(Object o)	删除集合中的 o
int size()	返回set中元素的个数
boolean isEmpty()	检测set是否为空，若为空则返回true，否则返回false
Object[] toArray()	将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)	检查set中是否包含集合c中全部元素，如果是，则返回true，否则返回false
boolean addAll(Collection<? extends E> c)	将集合c中的元素添加到set中，可以达到去重的效果

我们主要讲一下toArray方法

• 这个方法返回一个包含Set中所有元素的数组，所以，当我们需要遍历Set中的元素或对Set进行数组操作时，可以用toArray方法将Set转换为数组
• 如果一个方法的参数类型是数组，那么可以使用toArray方法将Set的元素转为数组，然后作为参数传递给方法

如果希望将元素转换为特定类型的数组，可以使用另一个重载的toArray方法：

<T> T[] toArray(T[] a);

• 这个方法允许我们指定要转换的数组类型，并将Set中的元素存储在指定类型的数组中。
  如果指定的数组大小足够大，那它将用来存储Set中的元素。而如果大小不足以存储所有元素，那么toArray方法就会创建一个新的数组，并返回它

来看下例子：

    public static void main(String[] args) {Set<String> colors = new HashSet<>();colors.add("red");colors.add("blue");colors.add("green");// 使用toArray方法将Set转换为数组Object[] colorsArray = colors.toArray();System.out.println("Set转换为数组：" + Arrays.toString(colorsArray));// 使用重载的toArray方法指定类型String[] colorsArray2 = colors.toArray(new String[colors.size()]);System.out.println("Set转换为指定类型的数组：" + Arrays.toString(colorsArray2));}

🍌TreeSet和HashSet的区别

Set底层结构	TreeSet	HashSet
底层结构	红黑树	哈希桶
插入/删除/查找的时间复杂度	O（logN）	O（1）
是否有序	关于Key有序	不一定有序
线程安全	不安全	不安全
插入/删除/查找区别	按照红黑树的特性来进行插入和删除	先计算key哈希地址，然后进行插入和删除
比较与覆写	key必须能够比较，否则会抛出ClassCastException异常	自定义类型需要覆写equals和hashCode方法
应用场景	需要Key有序的场景	不关心Key是否有序，需要更高的时间性能