一、图的遍历
从图中的某个顶点出发,沿着某条搜索路径对图中的所有顶点进行访问,且,只访问一次的过程。
图的遍历比树的遍历复杂,因为要避免对顶点进行重复访问,所以在图的遍历过程中,必须记下每个已访问过的顶点。
树的遍历:
- 先序遍历
- 中序遍历
- 后序遍历
- 层次遍历
图的遍历基本方法:
- 深度优先搜索
- 广度优先搜索
1-1、深度优先搜索:DFS
示例:
深度遍历涉及到回溯,这是递归的思想。
时间复杂度:
深度优先遍历图的过程实质上是对某个顶点查找其邻接点的过程,其耗费的时间取决于所采用的存储结构。
图中的顶点数n,图中的边数e:
(1)当图用邻接矩阵表示时,查找所有顶点的邻接点所需时间为 O(n^2)。
(2)若以邻接表作为图的存储结构,则需要 O(e)的时间复杂度查找所有顶点的邻接点。因此,当以邻接表作为存储结构时,深度优先搜索遍历图的时间复杂度为 O(n + e)。
1-2、广度优先搜索BFS

将队头的元素和其所有的相邻节点入队列。
时间复杂度:
遍历图的过程,实质上是通过边找邻接点的过程,因此,广度优先搜索遍历图和深度优先搜索遍历图的运算时间复杂度相同。不同之处仅仅在于对定点的访问次序不同。
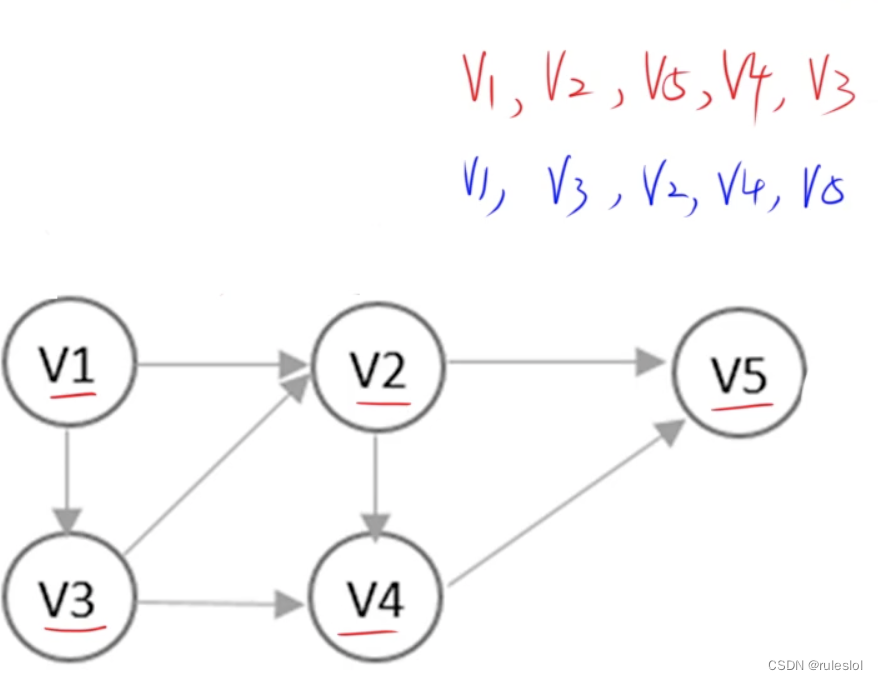
1-3、真题
真题1:

真题2:
 真题3:
真题3:

G中任意两个顶点之间均有边存在——完全图
无向连通图:
从图中任意顶点出发,可遍历图中所有顶点,
有向连通图:
从图中任意顶点出发,可遍历图中所有顶点,
真题4:

真题5:B、A

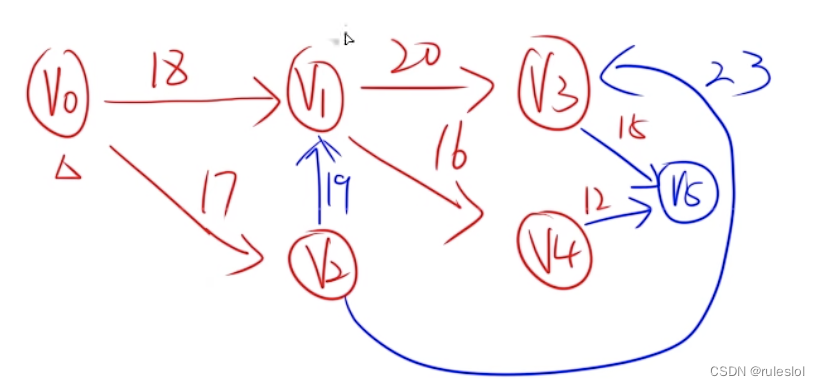
强连通图:从图中任意顶点出发,能够遍历图中所有节点。因为V5没有任何出度,所以不能从V5开始遍历,所以,不是强连通图。
真题6:
二、拓扑排序
2-1、AOV网(有向无环图)
有向图,以顶点表示活动,以有向边表示活动之间的优先关系,也是活动之间的制约关系。
在AOV网中不应该出现有向环。
2-2、拓扑排序
AOV网代表一个工程计划,AOV网的拓扑排序就是一个工程顺利完成的可行方案。AOV网的拓扑排序,方法如下:
1、在AOV网中选择一个入度为0(没有前驱)的顶点,输出它;
2、从网中删除该顶点及与该顶点有关的所有弧;
3、重复上下两步,直到网中不存在入度为0的顶点为止。
示例:

在AOV网的拓扑序列中,顶点Vi在Vj之前,则:
可能存在弧<Vi, Vj>,一定不存在弧<Vj, Vi>;Vi——>Vj
可能存在Vi到Vj的路径,一定不存在Vj到Vi的路径。Vi——>Vx——>Vj
2-3、真题
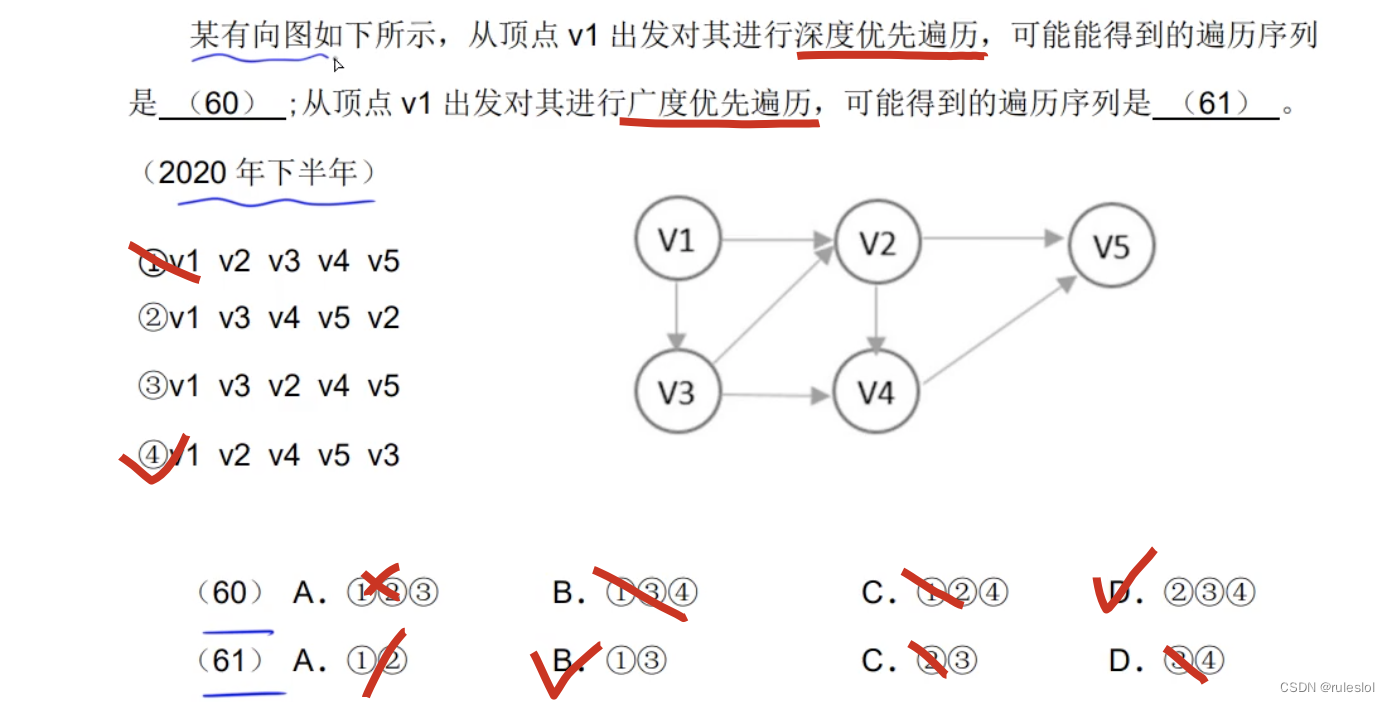
真题1:
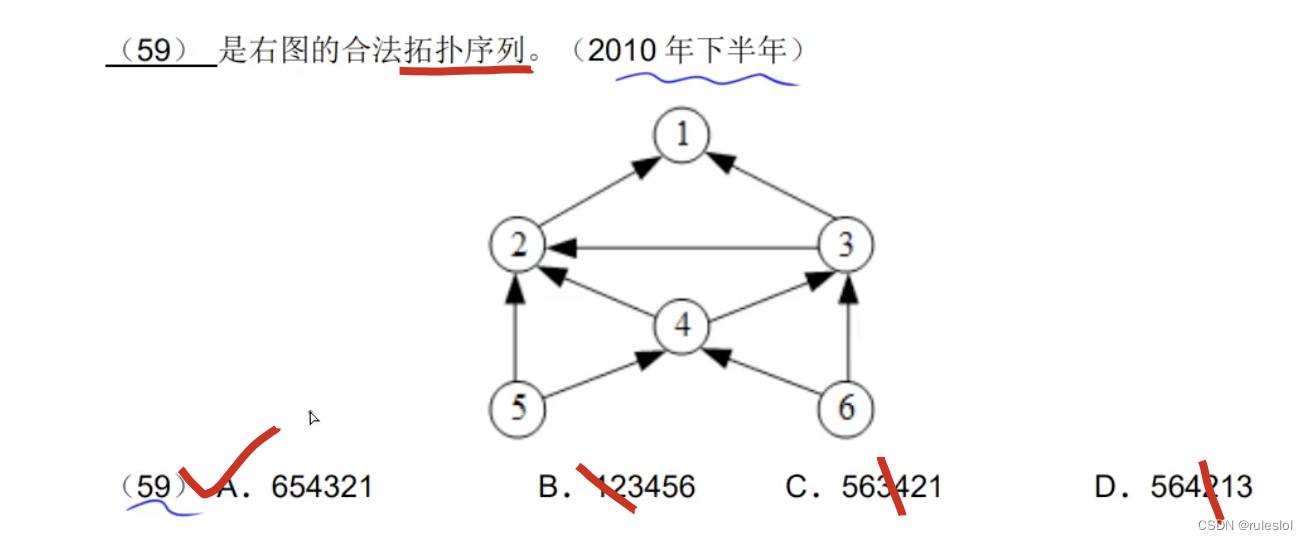
真题2:
 真题3:
真题3:

真题4:
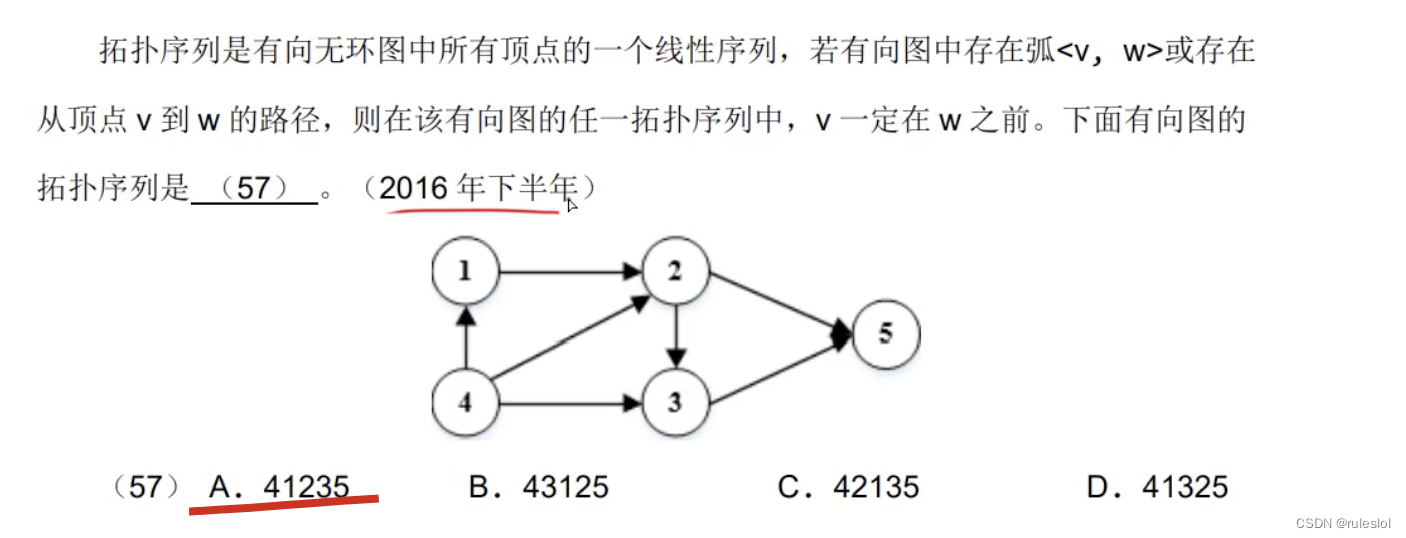 真题5:
真题5:







![[Linux开发工具]项目自动化构建工具-make/Makefile](http://pic.xiahunao.cn/[Linux开发工具]项目自动化构建工具-make/Makefile)



)

——认识泛型)






)

