上次咋们讲了前两个区间模型:1.最大不重叠区间数 2.不重叠区间最少分组数。今天我们就学习:最小区间覆盖问题、区间重叠最厚层数!
最小区间覆盖
先看三道题



那么,第1题,它是浮点数的题,也就要求首尾相同。第2题,是整数型,也就要求首尾差1。
大家思考思考如何规划这个算法。
算法
将所有区间按左坐标从小到大排序,顺序处理每一个区间。每次选择覆盖点s的区间中右坐标最大的区间,并将s更新为此区间右坐标,直到选择的区间包含t。
算法证明
显然该算法的准确性是一定的,一下证明该算法的最小性。


所以,证毕。
实现
选择区间使用线性扫描进行。排序(O(nlog n))+扫描(O(n))=O(nlog n)
整数覆盖
整数覆盖对应着第二题,下面给出代码
#include <bits/stdc++.h>
using namespace std;
const int N=109;
struct piece{int s,t;};
bool cmp(const piece& a,const piece& b){return a.s<b.s||a.s==b.s&&a.t<b.t;
}
piece d[N];
int main(){int i,j,n;cin>>n;for(i=0;i<n;i++) cin>>d[i].s>>d[i].t;sort(d,d+n,cmp);int S=1,T=100,cnt=0;for(i=0;i<n&&S<=T;i++){for(j=i;j<n&&d[j].s<=S;j++)if(d[j].t>d[i].t) i=j;if(d[i].s>S) break;S=d[i].t+1;cnt++; }if(S<=T) cout<<"sorry"<<endl;else cout<<cnt<<endl;return 0;
}当然,浮点数覆盖也就只改了double,S=d[i].t和i<n&&S<T还有if(S<T),而已。
区间重叠最厚层数
给一道例题把

这里我们要将一个“扫描算法”(不是扫描线)。长这样👇
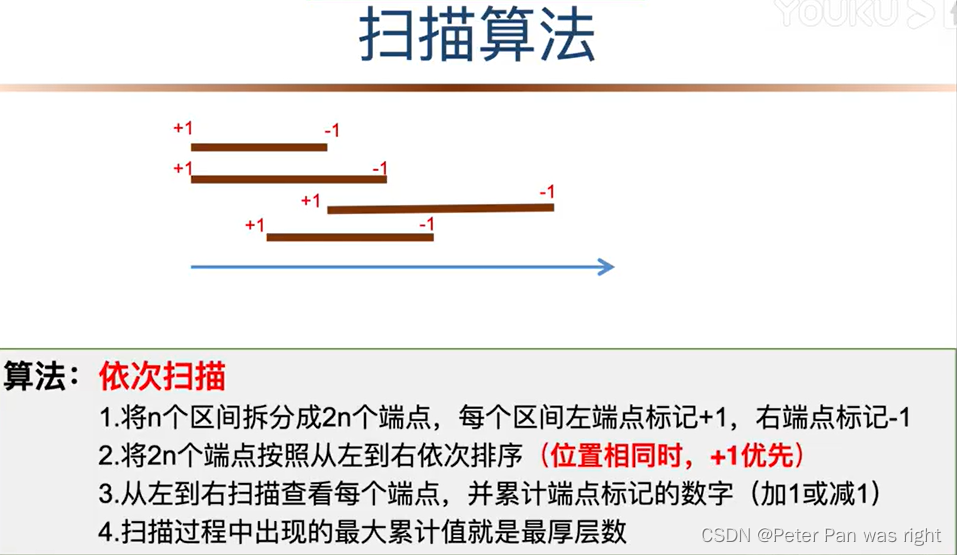
代码:
#include <bits/stdc++.h>
#define N 2005
using namespace std;
struct point{int pos,tag;};
bool cmp(const point&a,const point&b){return a.pos<b.pos||a.pos==b.pos&&a.tag>b.tag;
}
point d[N];
int main(){int n,cnt=0,ans=0;cin>>n;for(int i=0;i<n+n;i+=2){cin>>d[i].pos>>d[i+1].pos;d[i].tag=1;d[i+1].tag=-1;}sort(d,d+n+n,cmp);for(int i=0;i<n+n;i++){cnt+=d[i].tag;ans=max(ans,cnt);}cout<<ans<<endl;return 0;
}我们每一次涂修正带用两格的地方存pos和tag,tag指的是标记,pos指的是从几到几。
当然,还有一种加权的类型,比如说,你在[S,T]区间内要涂R层修正带,看下一题。
399
题目描述
你作为西佳佳部落的首领,今天将面临n场其他部落的挑衅,你需要调度投石器去抵御外敌。为了消灭部落i派来的敌人,你需要ri个投石器,在时间si到ti进行战斗。你的投石器每一场战役打完无需休息,直接可以投入下一场战斗。请问你至少需要制造多少个投石器就能抵御所有外敌?
#include <bits/stdc++.h>
#define N 20005
using namespace std;
struct point{int pos,tag;};
bool cmp(const point&a,const point&b){return a.pos<b.pos||a.pos==b.pos&&a.tag<b.tag;
}
point d[N];
int main(){int n,cnt=0,ans=0;cin>>n;for(int i=0;i<n+n;i+=2){int h1,h2,m1,m2;char ch;cin>>h1>>ch>>m1>>ch>>h2>>ch>>m2>>d[i].tag;d[i].pos=h1*60+m1;d[i+1].pos=h2*60+m2;d[i+1].tag=-d[i].tag;}sort(d,d+n+n,cmp);for(int i=0;i<n+n;i++){cnt+=d[i].tag;ans=max(ans,cnt);}cout<<ans<<endl;return 0;
}这里的tag变了哦。
希望这些对大家有用,三连必回。







)











