问题

冲击可以通过峭度指标来检测，是如何来检测的，可以给1个示例代码吗

思路

• 带冲击的信号其峭度指标>3
• 不带冲击的信号其峭度指标在3左右
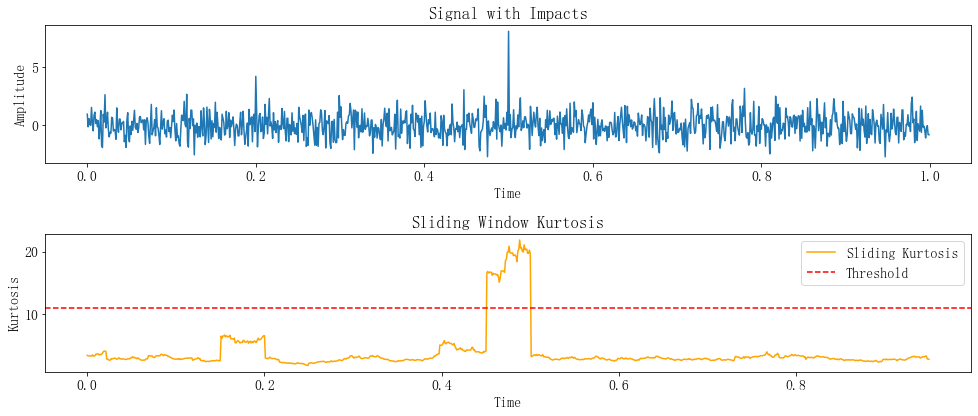
• 可以通过滑动窗来检测在哪一段

示例代码

带冲击的信号峭度指标值

import numpy as np
import matplotlib.pyplot as pltdef generate_signal_with_impact(impact_time=0.5, impact_magnitude=10, duration=1, sampling_rate=1000):"""生成含有单个冲击的信号:param impact_time: 冲击发生的时间，以秒为单位:param impact_magnitude: 冲击的幅度:param duration: 信号的总持续时间，以秒为单位:param sampling_rate: 采样率:return: 时间序列和信号值"""t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)signal = np.random.normal(0, 1, size=t.shape)  # 生成随机噪声信号impact_index = int(impact_time * sampling_rate)signal[impact_index] += impact_magnitude  # 在指定时间添加冲击return t, signaldef calculate_kurtosis(signal):"""计算信号的峭度:param signal: 输入信号:return: 峭度值"""n = len(signal)mean = np.mean(signal)std_dev = np.std(signal)sum_diff = np.sum((signal - mean) ** 4)kurtosis = (n * sum_diff) / ((n - 1) * (n - 2) * (std_dev ** 4))return kurtosis# 生成含有冲击的信号
t, signal = generate_signal_with_impact()# 计算信号的峭度
kurtosis_value = calculate_kurtosis(signal)
print(f"Kurtosis of the signal: {kurtosis_value}")# 绘制信号
plt.figure(figsize=(10, 4))
plt.plot(t, signal, label='Signal with Impact')
plt.title(f"Signal and its Kurtosis: {kurtosis_value:.2f}")
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.legend()
plt.show()

Kurtosis of the signal: 12.830772158435776

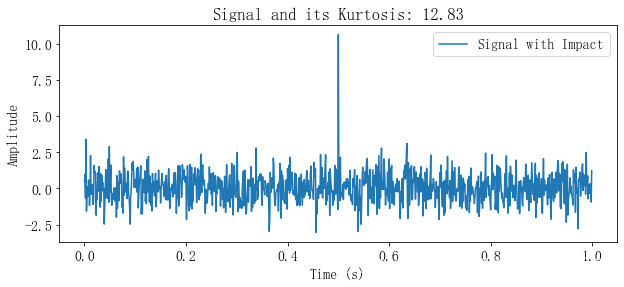
不带冲击的信号峭度指标值

import numpy as np
import matplotlib.pyplot as pltdef generate_signal_with_impact(impact_time=0.5, impact_magnitude=10, duration=1, sampling_rate=1000):"""生成含有单个冲击的信号:param impact_time: 冲击发生的时间，以秒为单位:param impact_magnitude: 冲击的幅度:param duration: 信号的总持续时间，以秒为单位:param sampling_rate: 采样率:return: 时间序列和信号值"""t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)signal = np.random.normal(0, 1, size=t.shape)  # 生成随机噪声信号impact_index = int(impact_time * sampling_rate)
#     signal[impact_index] += impact_magnitude  # 在指定时间添加冲击return t, signaldef calculate_kurtosis(signal):"""计算信号的峭度:param signal: 输入信号:return: 峭度值"""n = len(signal)mean = np.mean(signal)std_dev = np.std(signal)sum_diff = np.sum((signal - mean) ** 4)kurtosis = (n * sum_diff) / ((n - 1) * (n - 2) * (std_dev ** 4))return kurtosis# 生成含有冲击的信号
t, signal = generate_signal_with_impact()# 计算信号的峭度
kurtosis_value = calculate_kurtosis(signal)
print(f"Kurtosis of the signal: {kurtosis_value}")# 绘制信号
plt.figure(figsize=(10, 4))
plt.plot(t, signal, label='Signal with Impact')
plt.title(f"Signal and its Kurtosis: {kurtosis_value:.2f}")
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.legend()
plt.show()

Kurtosis of the signal: 3.0646772222342067

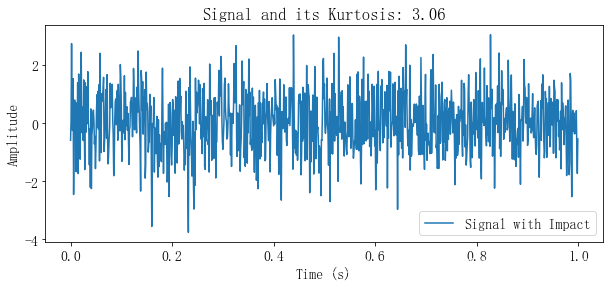
基于滑动窗的冲击信号检测

import numpy as np
import matplotlib.pyplot as pltdef generate_signal_with_impacts(impacts=[(0.2, 5), (0.5, 7)], sampling_rate=1000, duration=1):"""生成含有多个冲击的信号:param impacts: 冲击列表，每个元素为(冲击位置, 冲击幅度):param sampling_rate: 采样率:param duration: 信号持续时间:return: 时间数组和信号数组"""t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)signal = np.random.normal(0, 1, size=t.shape)  # 生成随机噪声信号for impact_position, impact_magnitude in impacts:impact_index = int(len(t) * impact_position)signal[impact_index] += impact_magnitude  # 添加冲击return t, signaldef calculate_sliding_kurtosis(signal, window_size=50):"""计算信号的滑动窗口峭度:param signal: 输入信号:param window_size: 滑动窗口大小:return: 峭度值数组"""kurtosis_values = []for i in range(len(signal) - window_size + 1):window = signal[i:i + window_size]n = len(window)mean = np.mean(window)std_dev = np.std(window)sum_diff = np.sum((window - mean) ** 4)kurtosis = (n * sum_diff) / ((n - 1) * (n - 2) * (std_dev ** 4))kurtosis_values.append(kurtosis)return np.array(kurtosis_values)# 生成信号
t, signal = generate_signal_with_impacts()# 计算滑动窗口峭度
kurtosis_values = calculate_sliding_kurtosis(signal)# 绘制信号和峭度
plt.figure(figsize=(14, 6))plt.subplot(2, 1, 1)
plt.plot(t, signal, label='Signal')
plt.title('Signal with Impacts')
plt.xlabel('Time')
plt.ylabel('Amplitude')plt.subplot(2, 1, 2)
plt.plot(t[:len(kurtosis_values)], kurtosis_values, label='Sliding Kurtosis', color='orange')
plt.axhline(y=np.mean(kurtosis_values) + 2*np.std(kurtosis_values), color='r', linestyle='--', label='Threshold')
plt.title('Sliding Window Kurtosis')
plt.xlabel('Time')
plt.ylabel('Kurtosis')plt.tight_layout()
plt.legend()
plt.show()