1. lim x − > 0 s i n ( 1 x ) \lim\limits_{x ->0}sin(\frac{1}{x}) x−>0limsin(x1)的极限不存在
取数列f(x), x n = 1 2 n Π − Π 2 x_n=\frac{1}{2nΠ-\frac{Π}{2}} xn=2nΠ−2Π1和 y n = 1 2 n Π + Π 2 y_n=\frac{1}{2nΠ+\frac{Π}{2}} yn=2nΠ+2Π1
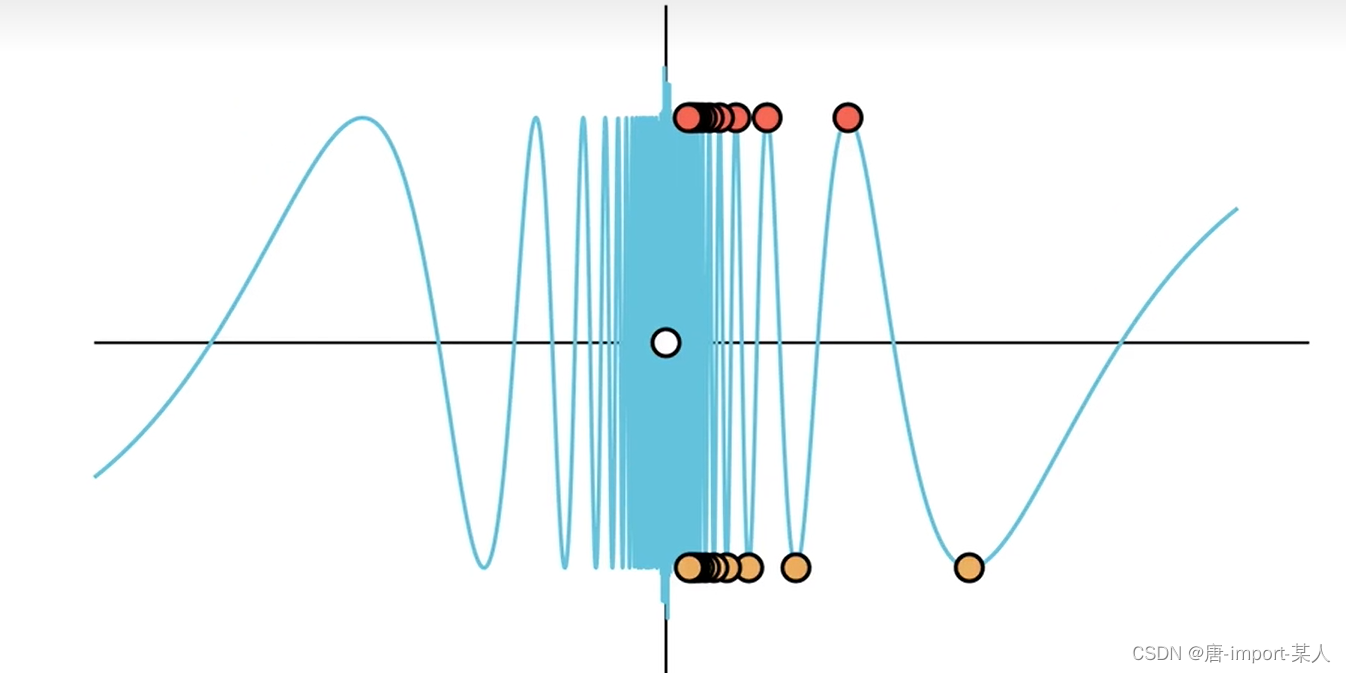
lim x − > ∞ s i n ( x n ) = lim x − > 0 s i n ( 1 2 n Π − Π 2 ) = − 1 \lim\limits_{x->∞}sin(x_n)=\lim\limits_{x->0}sin(\frac{1}{2nΠ-\frac{Π}{2}})=-1 x−>∞limsin(xn)=x−>0limsin(2nΠ−2Π1)=−1
lim x − > ∞ s i n ( y n ) = lim x − > 0 s i n ( 1 2 n Π + Π 2 ) = 1 \lim\limits_{x->∞}sin(y_n)=\lim\limits_{x->0}sin(\frac{1}{2nΠ+\frac{Π}{2}})=1 x−>∞limsin(yn)=x−>0limsin(2nΠ+2Π1)=1
lim x − > ∞ x n = 0 , x n ≠ 0 lim y − > ∞ y n = 0 , y n ≠ 0 lim x − > ∞ s i n ( x n ) ≠ lim x − > ∞ s i n ( y n ) } = > lim x − > 0 s i n ( 1 x ) 极限不存在 \begin{rcases} \lim\limits_{x->∞}x_n=0,x_n≠0\\ \lim\limits_{y->∞}y_n=0,y_n≠0\\ \lim\limits_{x->∞}sin(x_n)≠\lim\limits_{x->∞}sin(y_n) \end{rcases}=>\lim\limits_{x ->0}sin(\frac{1}{x})极限不存在 x−>∞limxn=0,xn=0y−>∞limyn=0,yn=0x−>∞limsin(xn)=x−>∞limsin(yn)⎭ ⎬ ⎫=>x−>0limsin(x1)极限不存在
2. lim x − > 0 s i n ( x ) \lim\limits_{x ->0}sin(x) x−>0limsin(x)的极限不存在
lim x − > ∞ s i n ( x n ) = lim x − > 0 s i n ( 2 n Π − Π 2 ) = − 1 \lim\limits_{x->∞}sin(x_n)=\lim\limits_{x->0}sin(2nΠ-\frac{Π}{2})=-1 x−>∞limsin(xn)=x−>0limsin(2nΠ−2Π)=−1
lim x − > ∞ s i n ( y n ) = lim x − > 0 s i n ( 2 n Π + Π 2 ) = 1 \lim\limits_{x->∞}sin(y_n)=\lim\limits_{x->0}sin({2nΠ+\frac{Π}{2}})=1 x−>∞limsin(yn)=x−>0limsin(2nΠ+2Π)=1
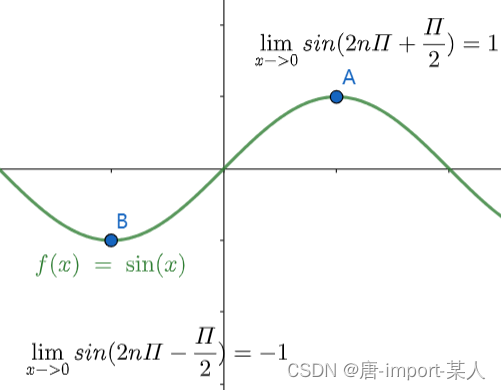
lim x − > ∞ x n = 0 , x n ≠ 0 lim y − > ∞ y n = 0 , y n ≠ 0 lim x − > ∞ s i n ( x n ) ≠ lim x − > ∞ s i n ( y n ) } = > lim x − > ∗ s i n ( x ) 极限不存在 \begin{rcases} \lim\limits_{x->∞}x_n=0,x_n≠0\\ \lim\limits_{y->∞}y_n=0,y_n≠0\\ \lim\limits_{x->∞}sin(x_n)≠\lim\limits_{x->∞}sin(y_n) \end{rcases}=>\lim\limits_{x ->*}sin(x)极限不存在 x−>∞limxn=0,xn=0y−>∞limyn=0,yn=0x−>∞limsin(xn)=x−>∞limsin(yn)⎭ ⎬ ⎫=>x−>∗limsin(x)极限不存在

)

)


)












)