内容参考于:三分钟音乐社
上一个内容:音值组合法(二)
力度记号:简谱里什么意思,五线谱也完全是什么意思,p越多就越弱,f越多就越强,然后这些渐强、渐弱、sf、fp这些标记都是与简谱一模一样的意思(力度记号)

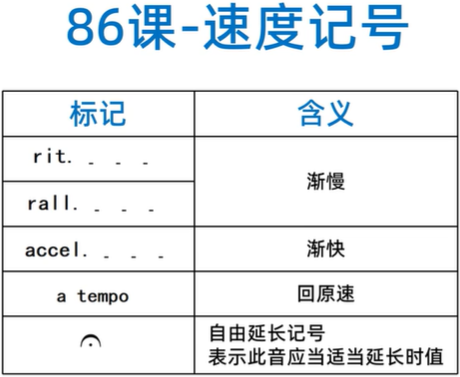
速度记号:rit、rall就表示渐慢,accel就是渐快,a tempo表示回原速(速度记号)
反复记号:反复记号(二)D.C.、D.S.、Fine、Coda、反复记号(一)反复、跳房子
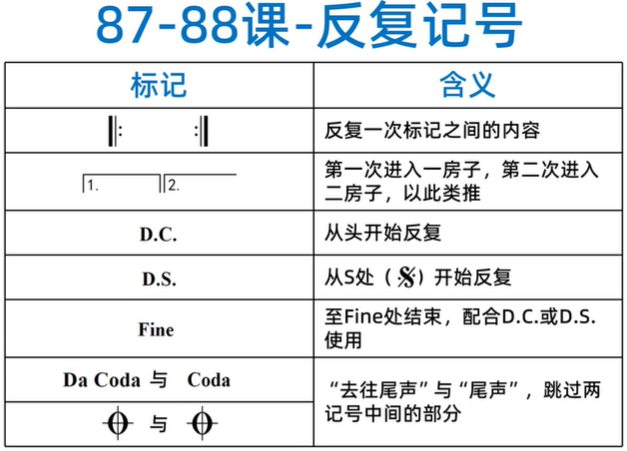
五线谱版:
区间反复:

跳房子的反复:

DC与Fine的反复:

DC与da coda、coda:

DS与Fine的反复:

DS与da coda、coda:

震音、音型反复、小节反复:
简谱版

五线谱版
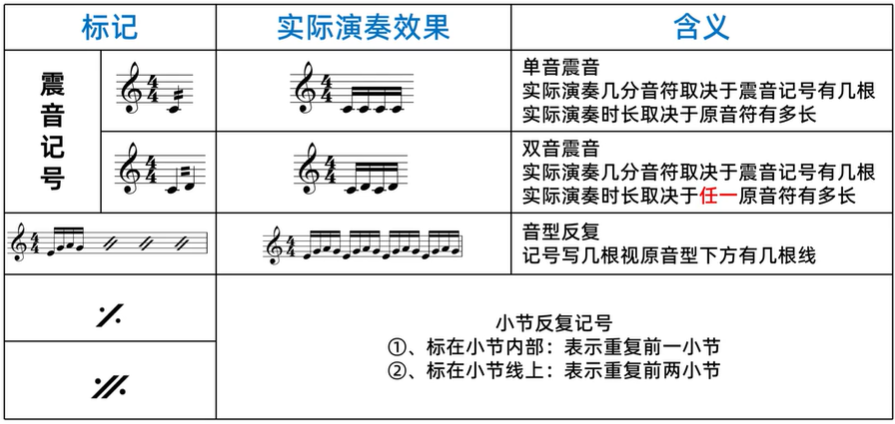
演奏记号:(记号说明)

换气:

跳音、断音:小黑三角形,它在简谱里叫跳音或者断音都可以,在五线谱里,跳音和断音是两个东西

五线谱的跳音和断音:

简谱里有高音点,所以简谱里不能用小黑点表示跳音,所以直接用小黑三角形表示跳音和断音
![]()
五线谱里跳音的意思:

五线谱里断音的意思:断音比跳音更加短促一些

连跳音:

保持音:

滑音、刮奏、琶音,这些东西的造型和意义,在五线谱里是完全一样的

例子:

级进、跳进、经过音、辅助音:装饰音记号(一)级进、跳进、经过音、辅助音,完全是概念性的东西,跟用什么谱都没任何关系

助音的四种类型:,完全是概念性的东西,跟用什么谱都没任何关系(助音的四种类型)

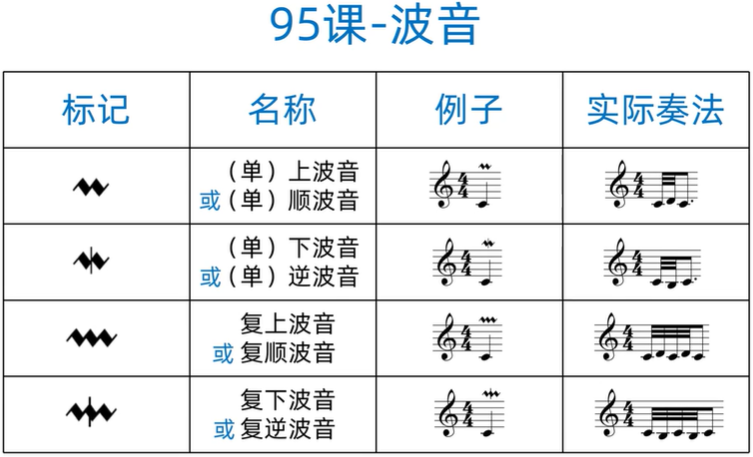
波音、回音、颤音、倚音:它们在简谱里的意义与造型完全与五线谱一样(波音、回音、颤音、倚音)
五线谱里的波音:
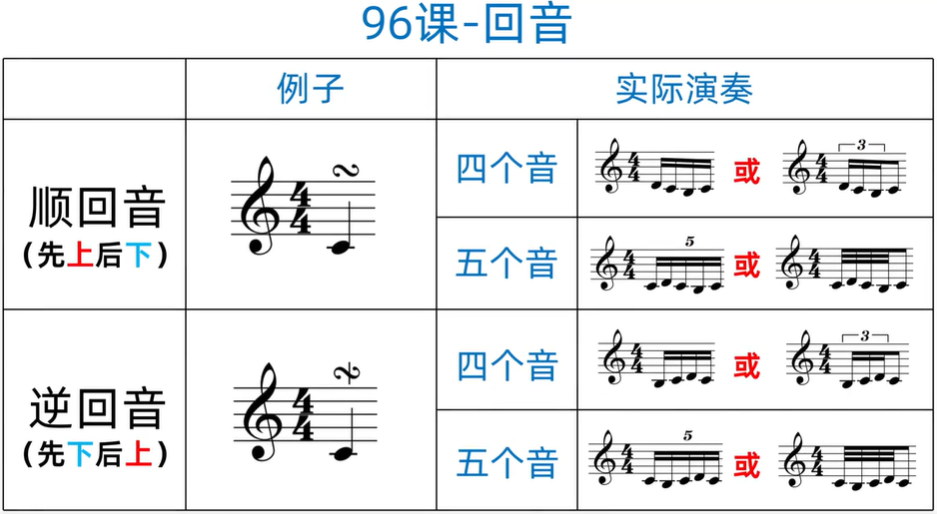
五线谱里的回音:
五线谱里的颤音:

五线谱里的倚音:倚音分短倚音与长倚音,长倚音已经没有意义了,为什么没有意义需要先看(倚音)

下图红框位置有一个短斜线:这就是提醒我们这是短倚音,长倚音就没有这根斜线

下图红框圈出来的就是长倚音

长倚音的时值:

长倚音例子:第一个长倚音后面是一个二分音符,这就说明这个长倚音要占据二分音符的一半,也就是一个四分音符的长度

然后实际要弹的就是:如下图,可以看出实际奏法比长倚音的形式要好看许多,更加直观

长倚音例子:带附点的,也可以看出下方的写法更加直观,所以现在很少使用长倚音了,现在说的倚音都是短倚音,短倚音不需要计算我要占据后面这个音符的几分之几的时值,然后后面这个音符又剩下多少时值






 - 剪辑时如何找到合适的音乐?!)






的算法与源代码)






