A 修改矩阵
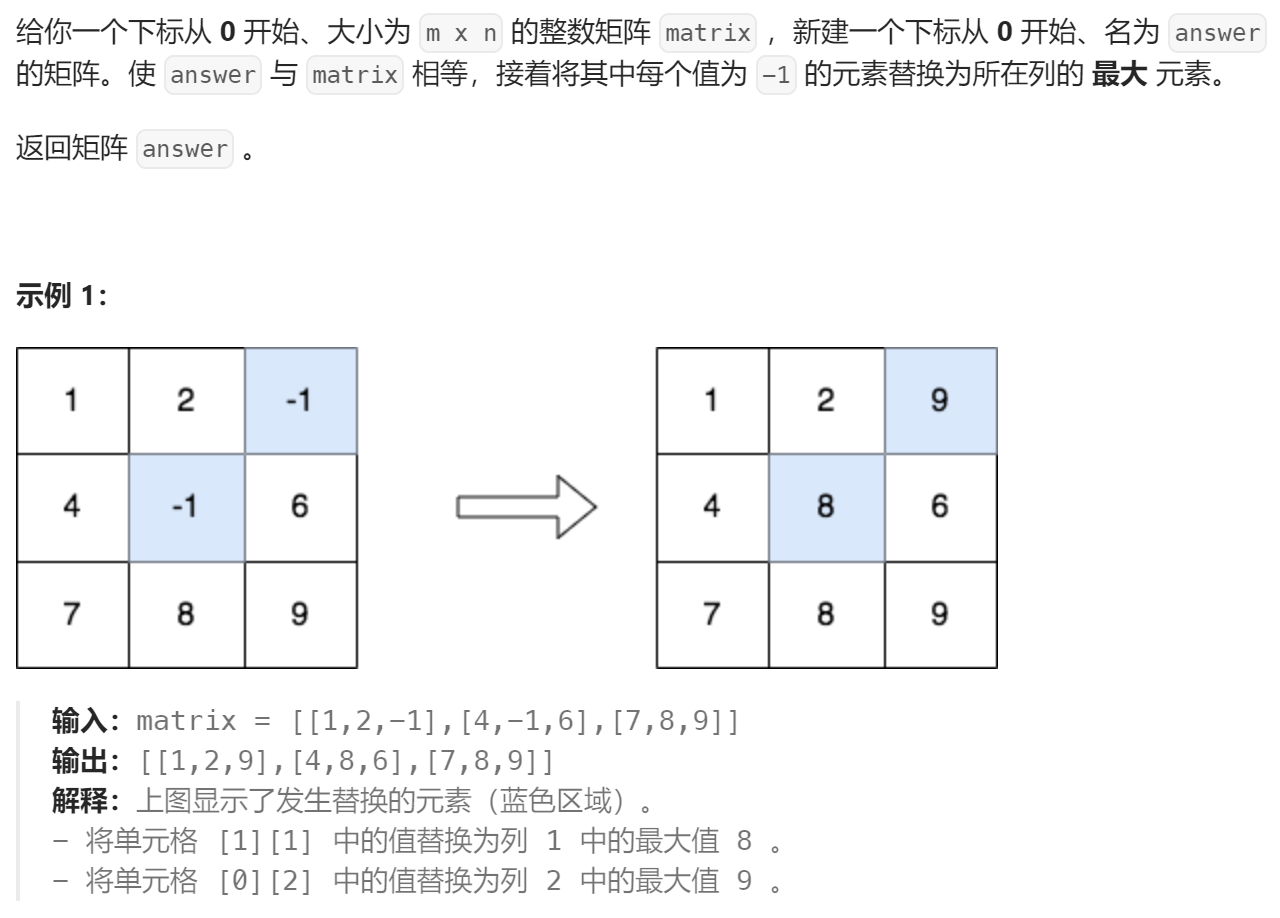
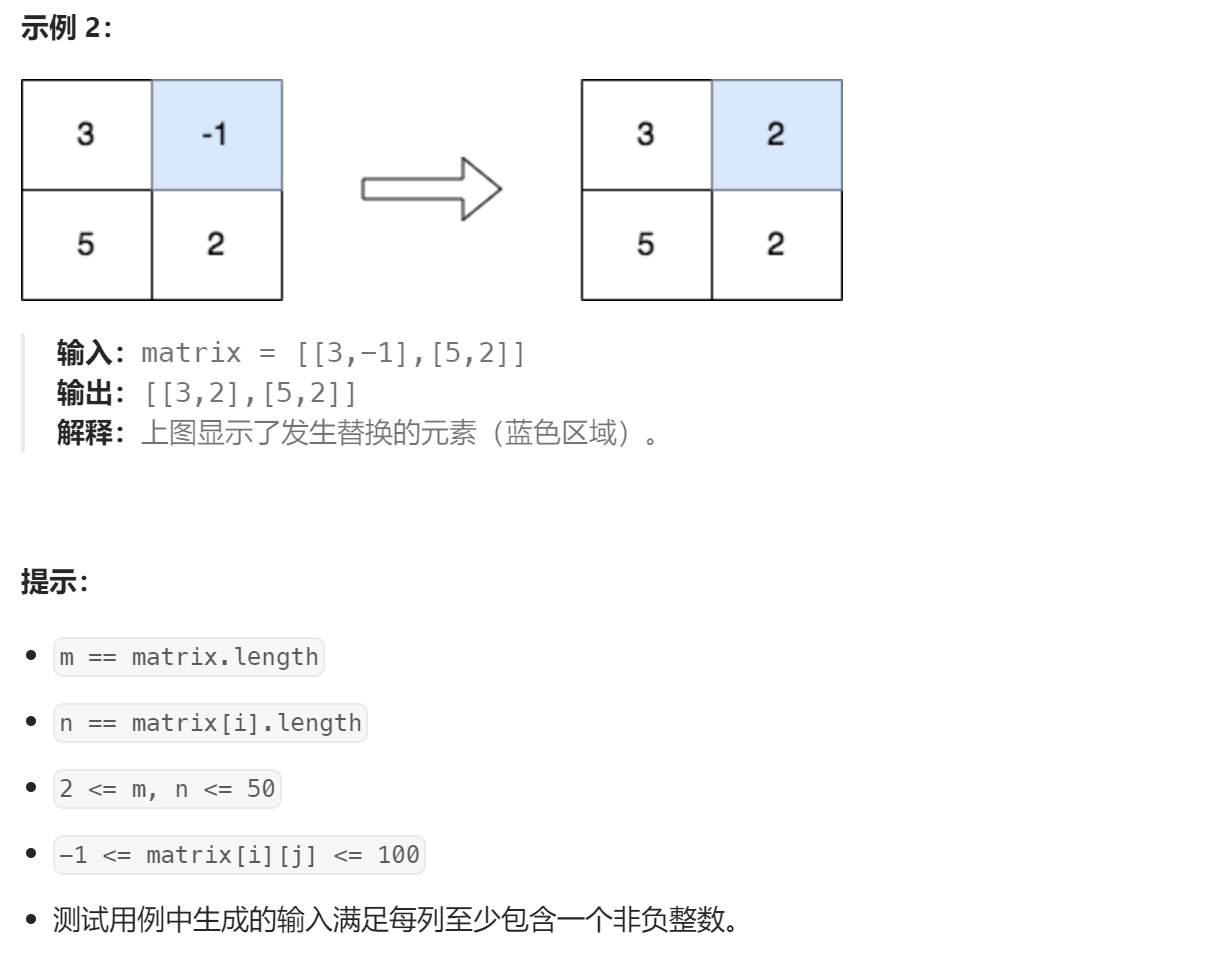
模拟
class Solution {
public:vector<vector<int>> modifiedMatrix(vector<vector<int>> &matrix) {int m = matrix.size(), n = matrix[0].size();vector<int> mx(n, INT32_MIN);for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)mx[j] = max(mx[j], matrix[i][j]);for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (matrix[i][j] == -1)matrix[i][j] = mx[j];return matrix;}
};
B 匹配模式数组的子数组数目 I


枚举 n u m s nums nums 中长为 m + 1 m+1 m+1 的子数组,判断是否匹配模式数组
class Solution {
public:int countMatchingSubarrays(vector<int> &nums, vector<int> &pattern) {int n = nums.size(), m = pattern.size();int res = 0;for (int i = 0, j = m; j < n; i++, j++) {int k = 0;for (; k < m; k++) {if (nums[k + i + 1] > nums[k + i] && pattern[k] != 1)break;if (nums[k + i + 1] == nums[k + i] && pattern[k] != 0)break;if (nums[k + i + 1] < nums[k + i] && pattern[k] != -1)break;}if (k == m)res++;}return res;}
};
C 回文字符串的最大数量


贪心:记录 w o r d s words words 中各字符总数,得到形成配对的字符数目 e v e n even even 和单一的字符数目 o d d odd odd,按 w o r d s words words 中字符串长短升序枚举字符串,判断能否形成回文字符串
class Solution {
public:int maxPalindromesAfterOperations(vector<string> &words) {vector<int> cnt(26);vector<int> li;for (auto &s: words) {li.push_back(s.size());for (auto c: s)cnt[c - 'a']++;}sort(li.begin(), li.end());int odd = 0, even = 0;//even:形成配对的字符数目,odd:单一的字符数目for (int i = 0; i < 26; i++)if (cnt[i]) {even += cnt[i] / 2 * 2;odd += cnt[i] % 2;}int res = 0;for (auto x: li) {if (x & 1) {if (even < x - 1)break;even -= x - 1;if (odd == 0) {if (even == 0)break;//需要拆一对配对字符even--;odd++;} elseodd--;} else {if (even < x)break;even -= x;}res++;}return res;}
};
D 匹配模式数组的子数组数目 II


滚动哈希 + 枚举:枚举 n u m s nums nums 中长为 m + 1 m+1 m+1 的子数组,用哈希判断是否匹配模式数组
class Solution {
public:int countMatchingSubarrays(vector<int> &nums, vector<int> &pattern) {int n = nums.size(), m = pattern.size();vector<int> li;for (int i = 0; i + 1 < n; i++) {if (nums[i + 1] > nums[i])li.push_back(1);else if (nums[i + 1] == nums[i])li.push_back(0);elseli.push_back(-1);}srand(time(0));//随机种子int e = 2333 + rand() % 100, p = 1e9 + rand() % 100;shash h1(li, e, p), h2(pattern, e, p);int res = 0;for (int i = 0; i + m - 1 < li.size(); i++)if (h1(i, i + m - 1) == h2(0, m - 1))res++;return res;}class shash {//滚动哈希模板public:using ll = long long;vector<ll> pres;vector<ll> epow;ll e, p;shash(vector<int> &s, ll e, ll p) {int n = s.size();this->e = e;this->p = p;pres = vector<ll>(n + 1);epow = vector<ll>(n + 1);epow[0] = 1;for (int i = 0; i < n; i++) {pres[i + 1] = (pres[i] * e + s[i]) % p;epow[i + 1] = (epow[i] * e) % p;}}ll operator()(int l, int r) {ll res = (pres[r + 1] - pres[l] * epow[r - l + 1] % p) % p;return (res + p) % p;}};
};











:使用 Scene API 和 Depth API 实现深度识别和环境遮挡)
)





