一、定义
索引(index)是帮助MySQL高效获取数据的数据结构(有序)。在数据之外,数据库系统还维护着满足特定查找算法的数据结构(B+树),这些数据结构以某种方式引用(指向)数据, 这样就可以在这些数据结构上实现高级查找算法,这种数据结构就是索引。
二、底层数据结构
MySQL默认使用的索引底层数据结构是B+树。为什么不使用二叉树和红黑树?主要原因就是不稳定,可能慢,可能快,因为时间复杂度的不平衡。
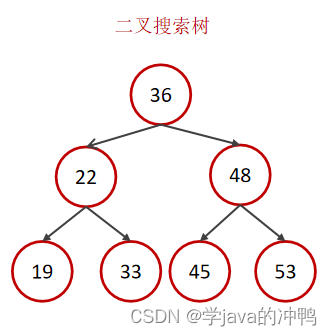
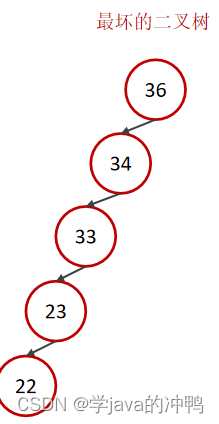
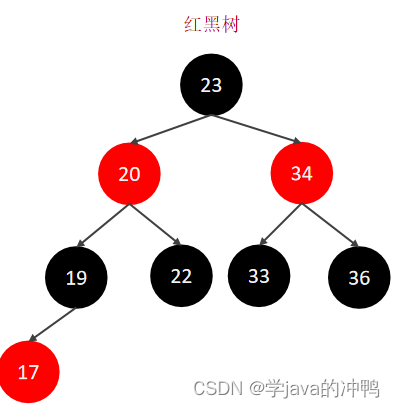
B-Tree,B树是一种多叉路衡查找树,相对于二叉树,B树每个节点可以有多个分支,即多叉。 以一颗最大度数(max-degree)为5(5阶)的b-tree为例,那这个B树每个节点最多存储4个key。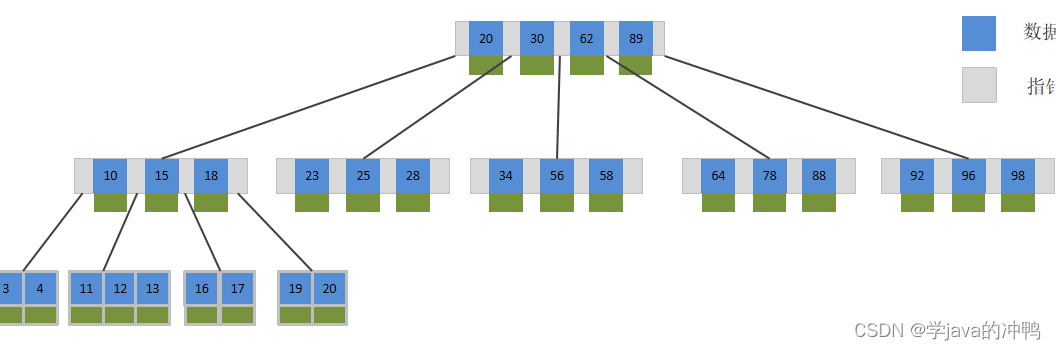
B+Tree是在BTree基础上的一种优化,使其更适合实现外存储索引结构,InnoDB存储引擎就是用B+Tree实现其索引结构。
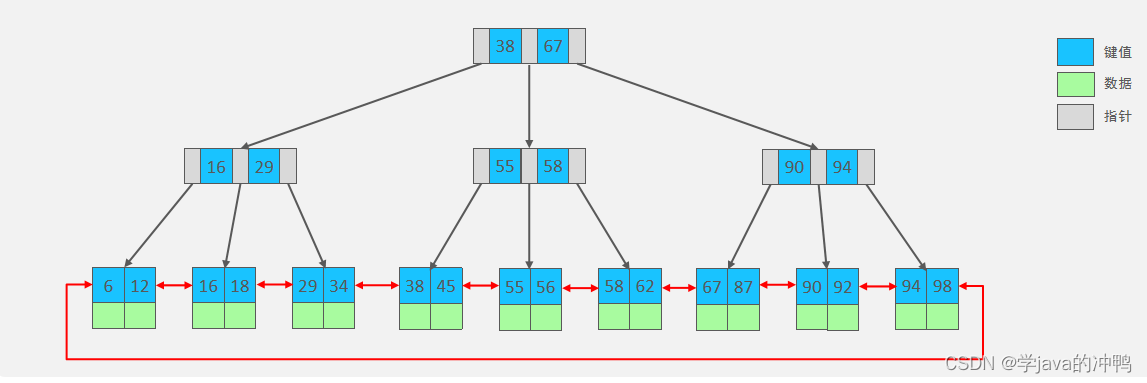
三、面试时的回答
面试官:了解过索引吗?(什么是索引)
候选人:嗯,索引在项目中还是比较常见的,它是帮助MySQL高效获取数据的数据结构,主要是用来提高数据检索的效率,降低数据库的IO成本,同时通过索引列对数据进行排序,降低数据排序的成本,也能降低了CPU的消耗。
面试官:索引的底层数据结构了解过嘛?
候选人:MySQL的默认的存储引擎InnoDB采用的B+树的数据结构来存储索引,选择B+树的主要的原因是:第一阶数更多,路径更短,第二个磁盘读写代价B+树更低,非叶子节点只存储指针,叶子阶段存储数据,第三是B+树便于扫库和区间查询,叶子节点是一个双向链表。
面试官:B树和B+树的区别是什么呢?
候选人:第一:在B树中,非叶子节点和叶子节点都会存放数据,而B+树的所有的数据都会出现在叶子节点,在查询的时候,B+树查找效率更加稳定。
第二:在进行范围查询的时候,B+树效率更高,因为B+树都在叶子节点存储,并且叶子节点是一个双向链表。
)





)
人工智能、机器学习、深度学习之间的关系)


)







