【北邮鲁鹏老师计算机视觉课程笔记】02 filter

1 图像的类型

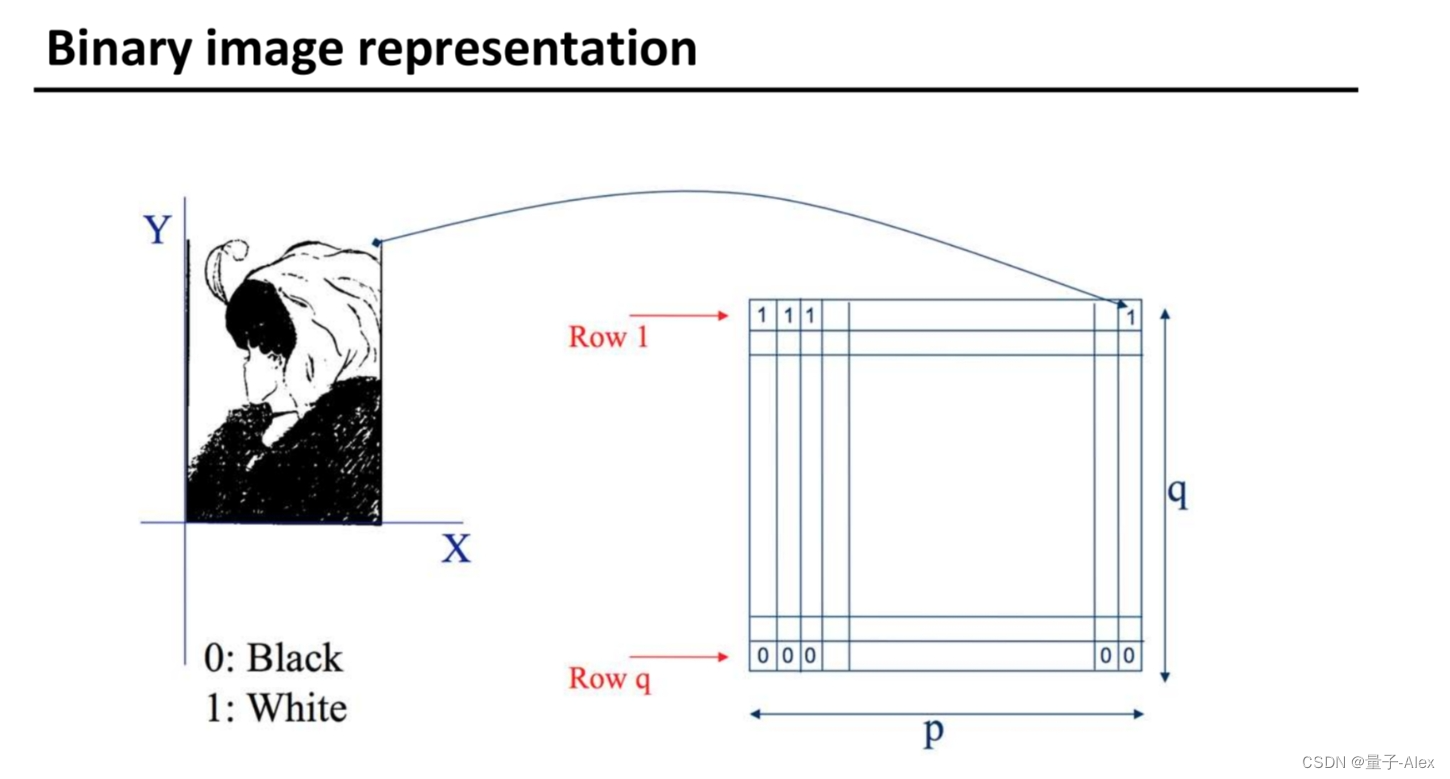
在这里插入图片描述
二进制图像：

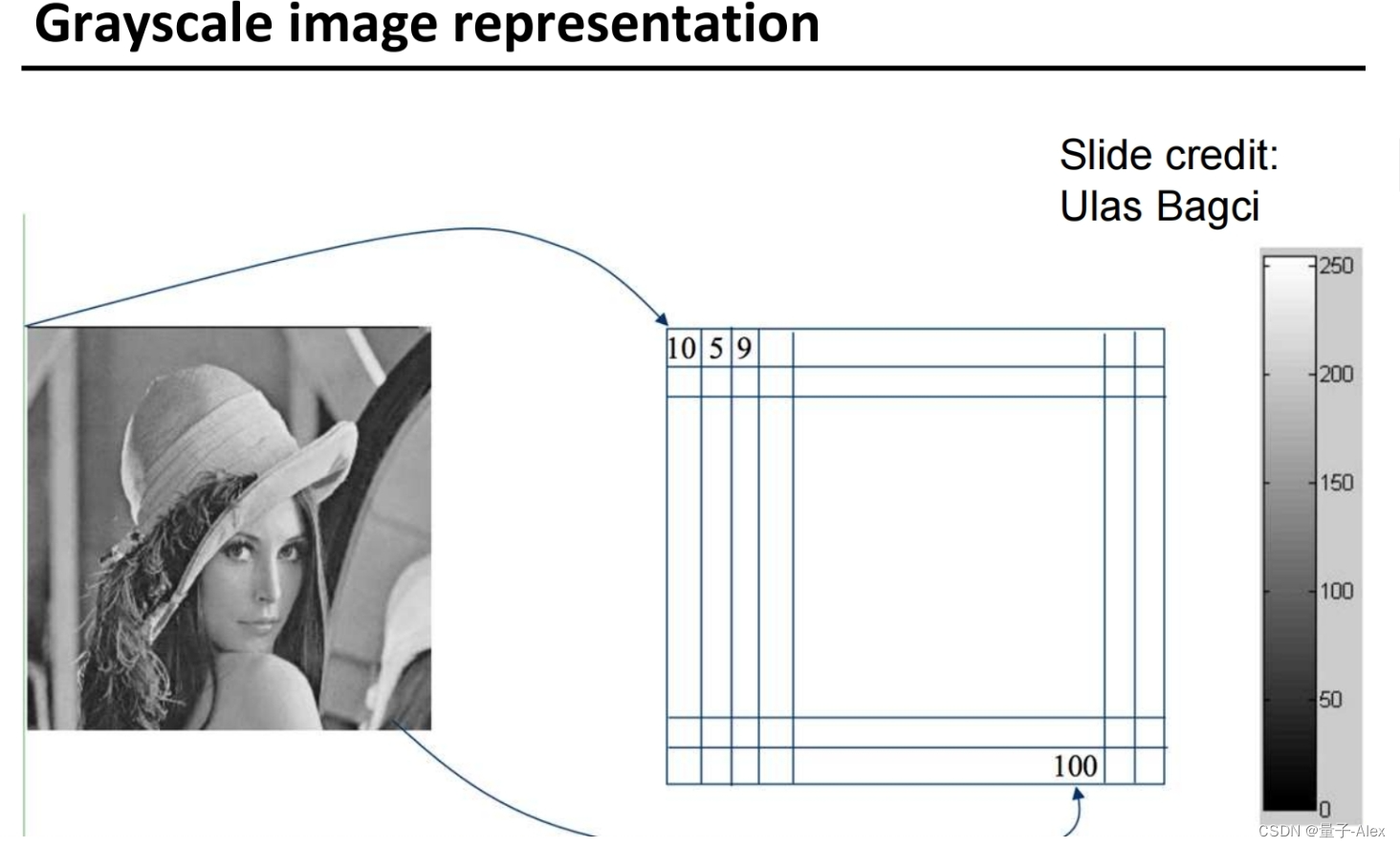
在这里插入图片描述
灰度图像：

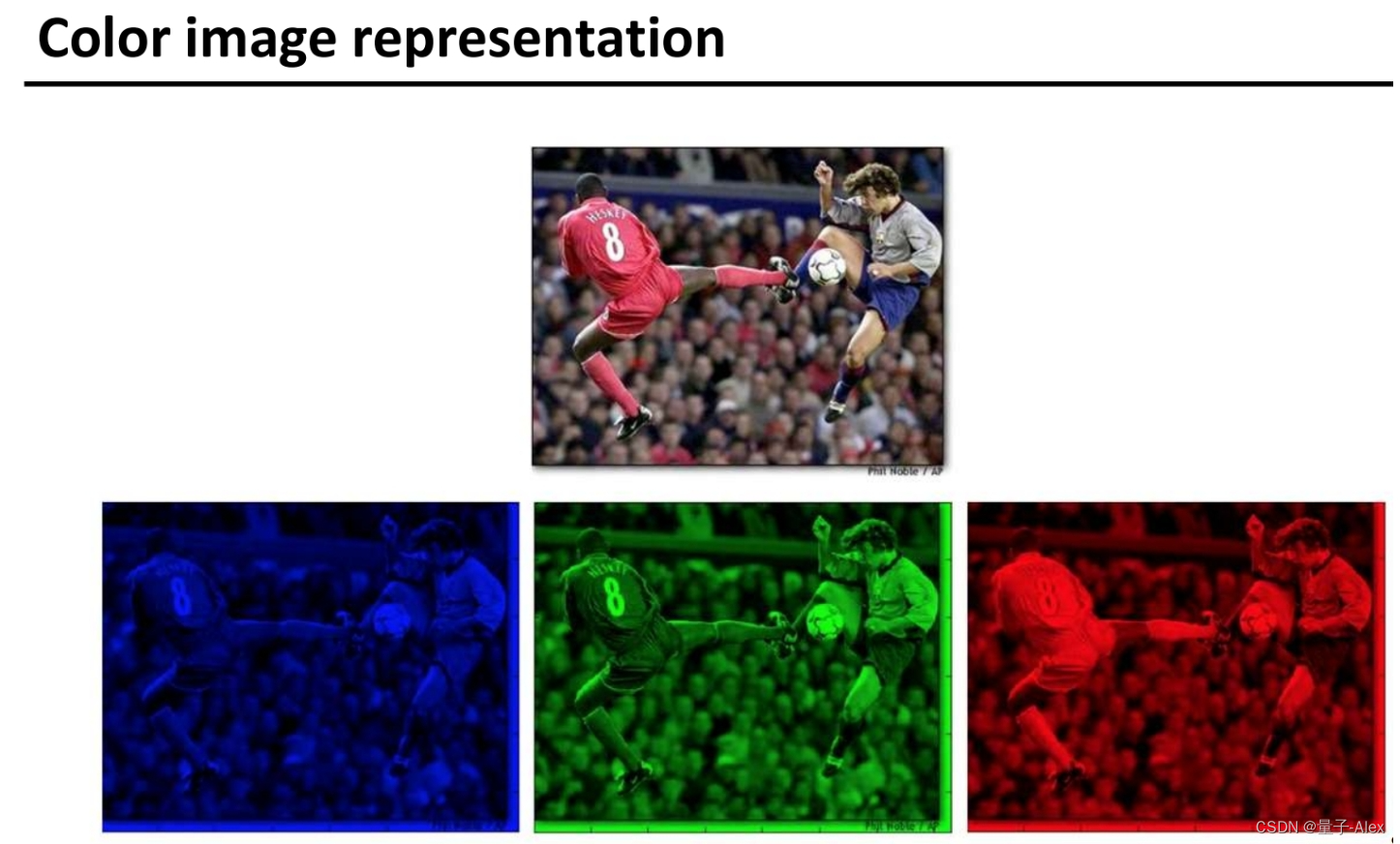
在这里插入图片描述

彩色图像：
在这里插入图片描述

2 任务：图像去噪

在这里插入图片描述

噪声点让我们看得难受是因为噪声点与周边像素差别很大

3 均值

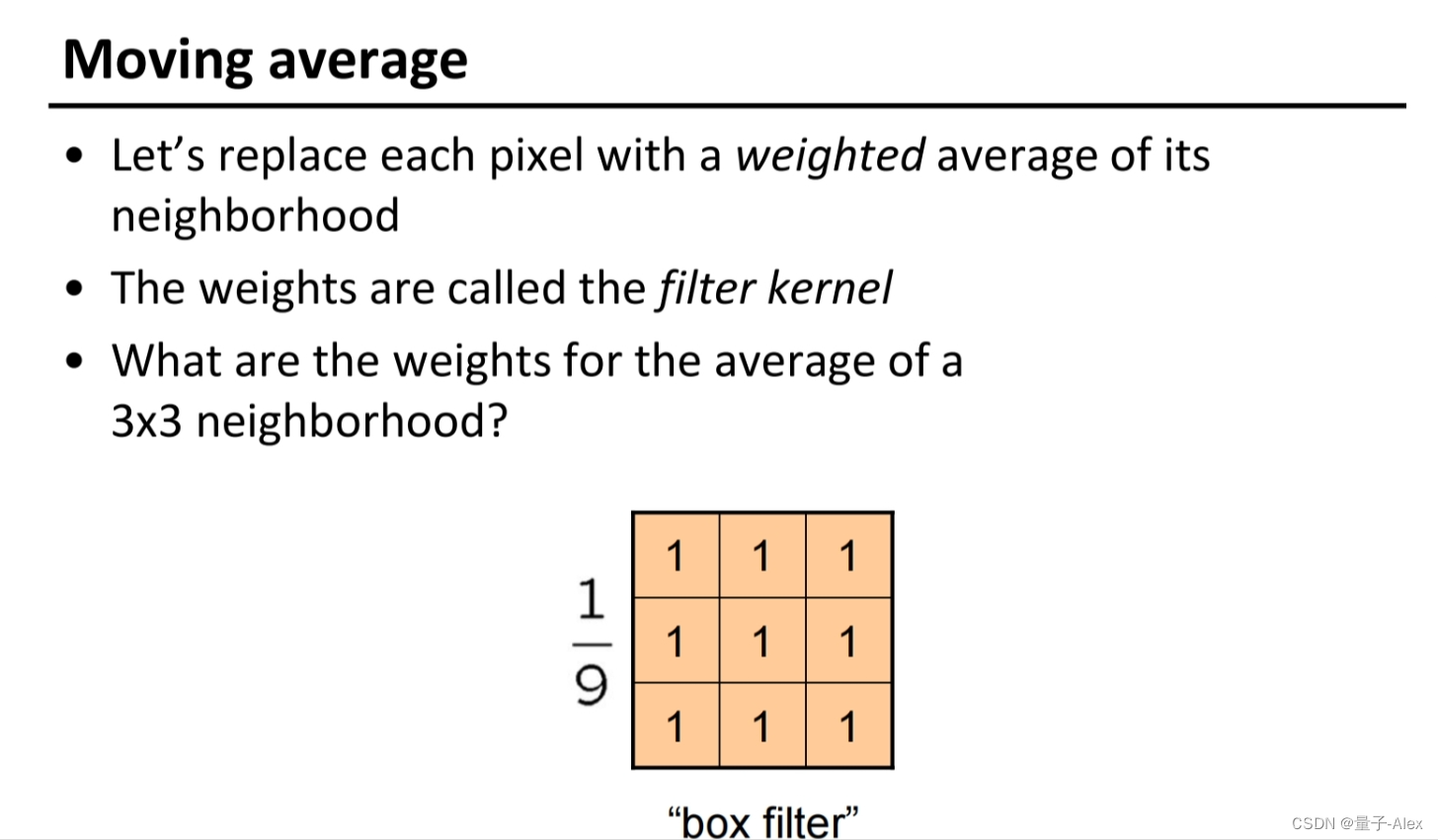
在这里插入图片描述

滤波核= 卷积核

4 卷积操作

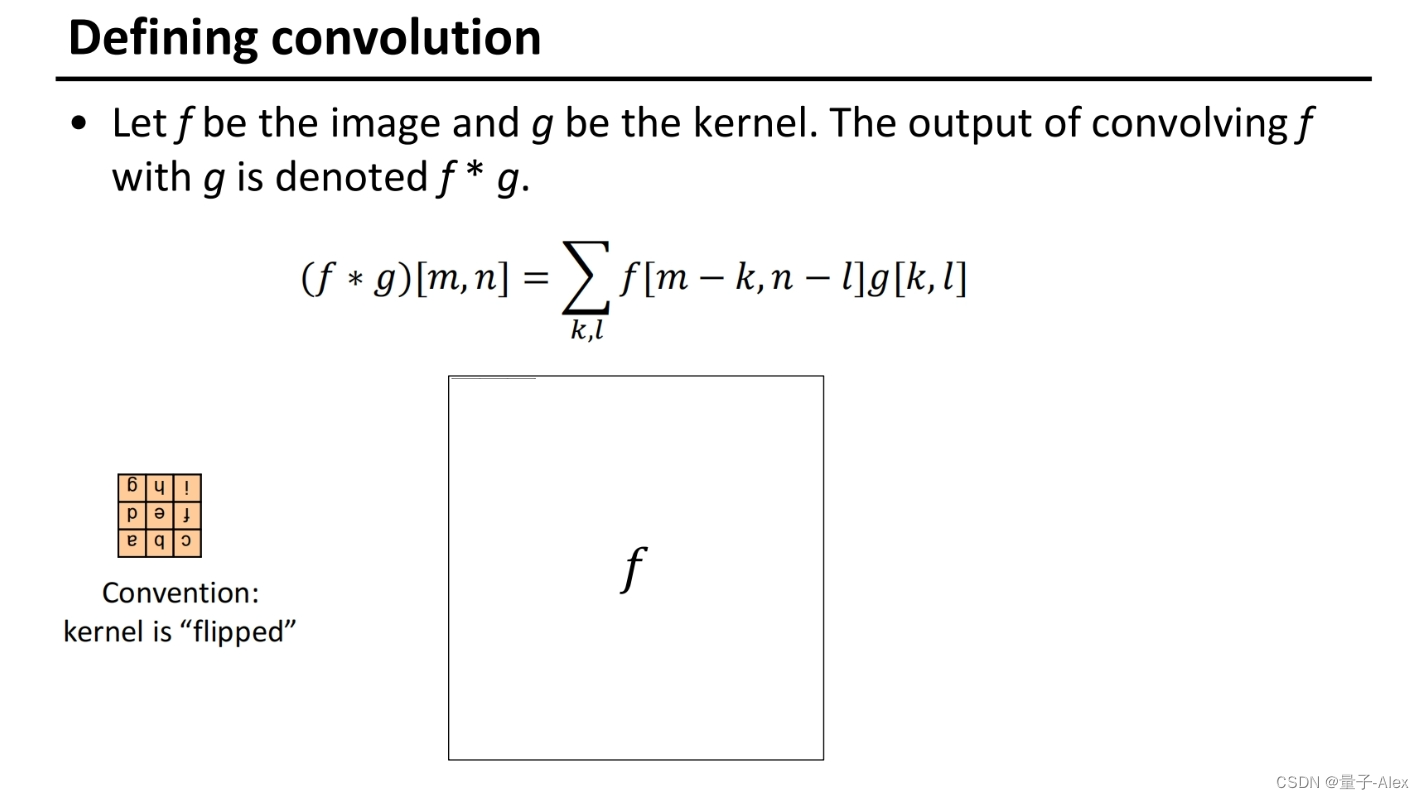
在这里插入图片描述
对应相乘再累加起来

卷积核记录了权值，把权值套到要卷积的目标图上，对应相乘

5 卷积的特性

在这里插入图片描述

线性和平移不变形

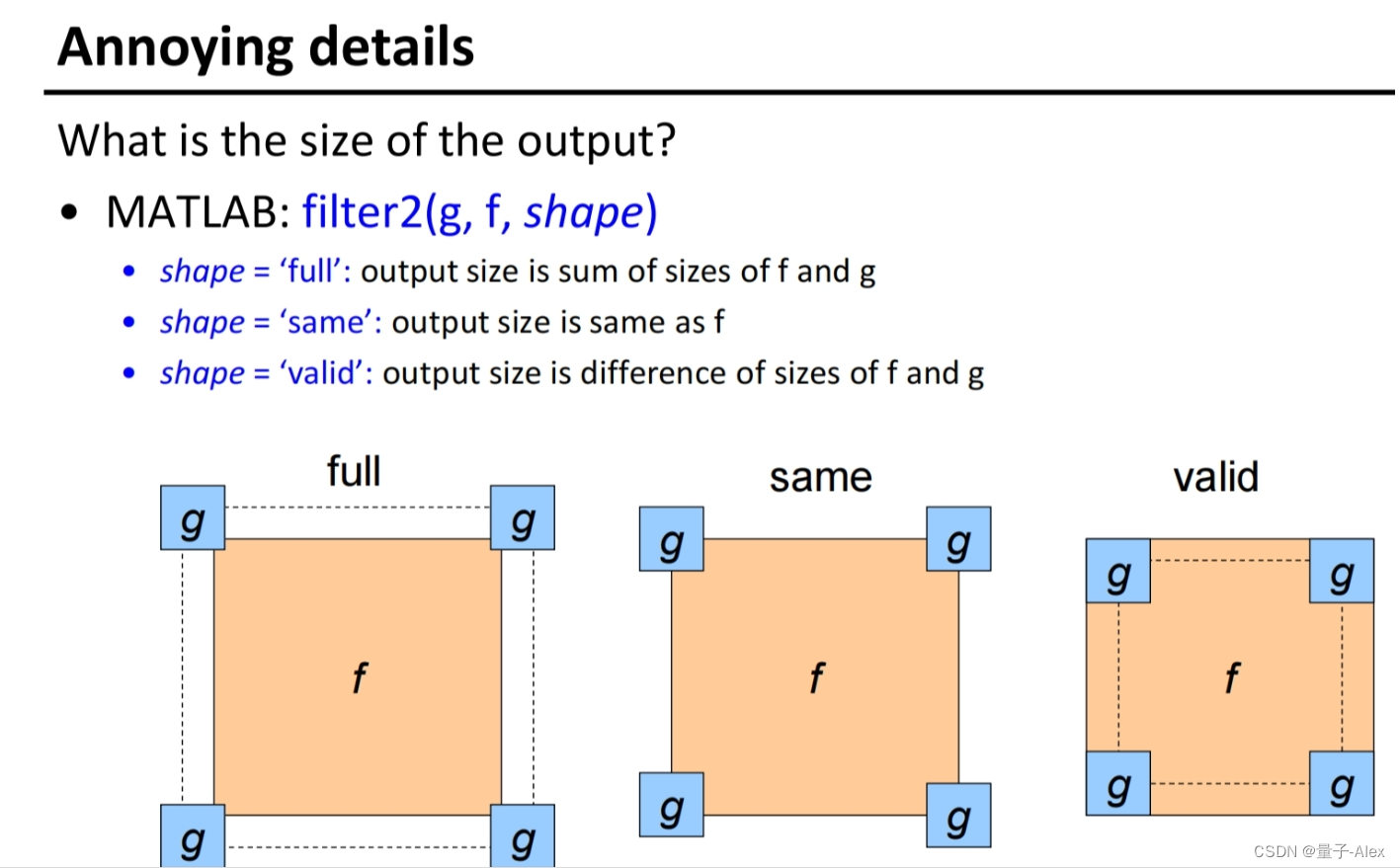
在这里插入图片描述

在这里插入图片描述

因为实际使用的时候卷积核是对称的，因此不要求翻转

真实运算的时候，对于没有像素的位置，要做填充，否则无法计算卷积，
最简单的办法，填充0。

在这里插入图片描述
在这里插入图片描述
填充是希望输入输出有固定的大小

6 卷积的应用

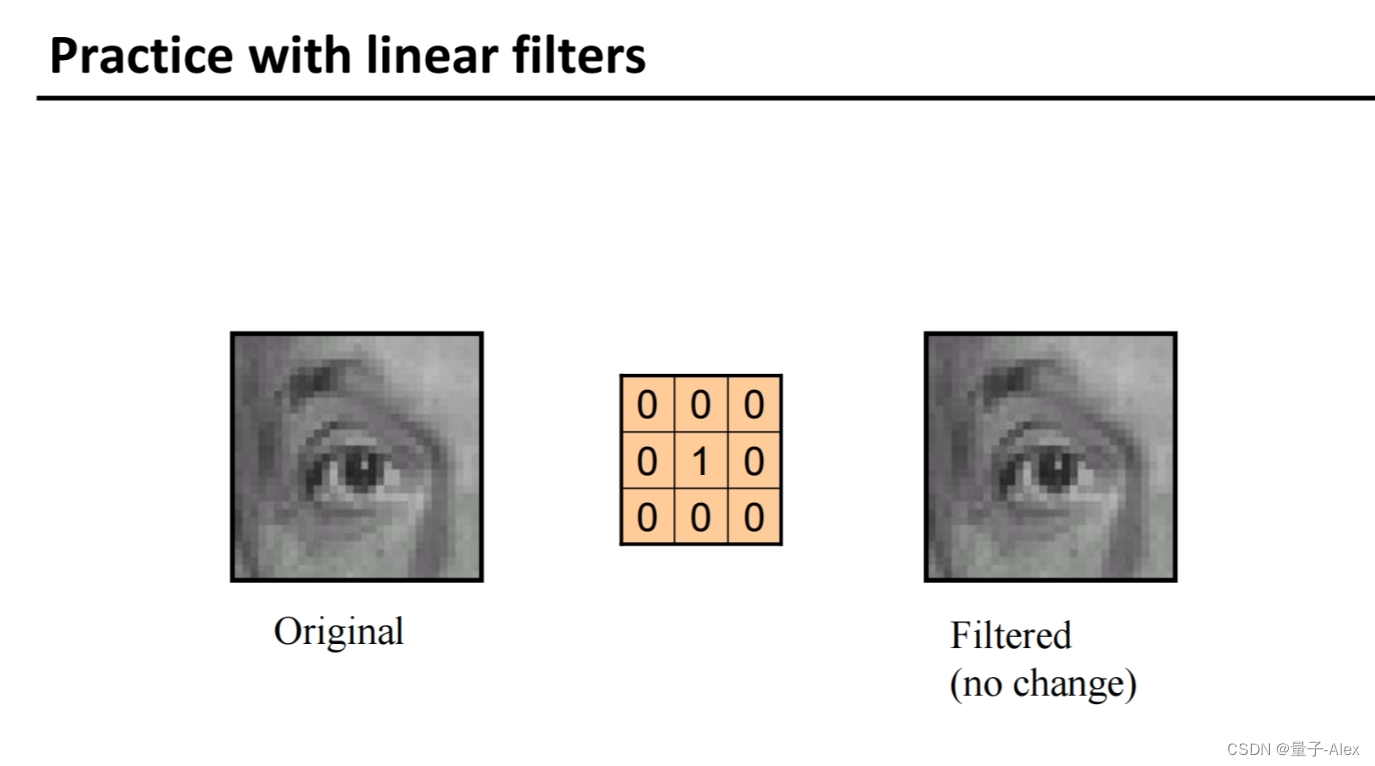
在这里插入图片描述
不变

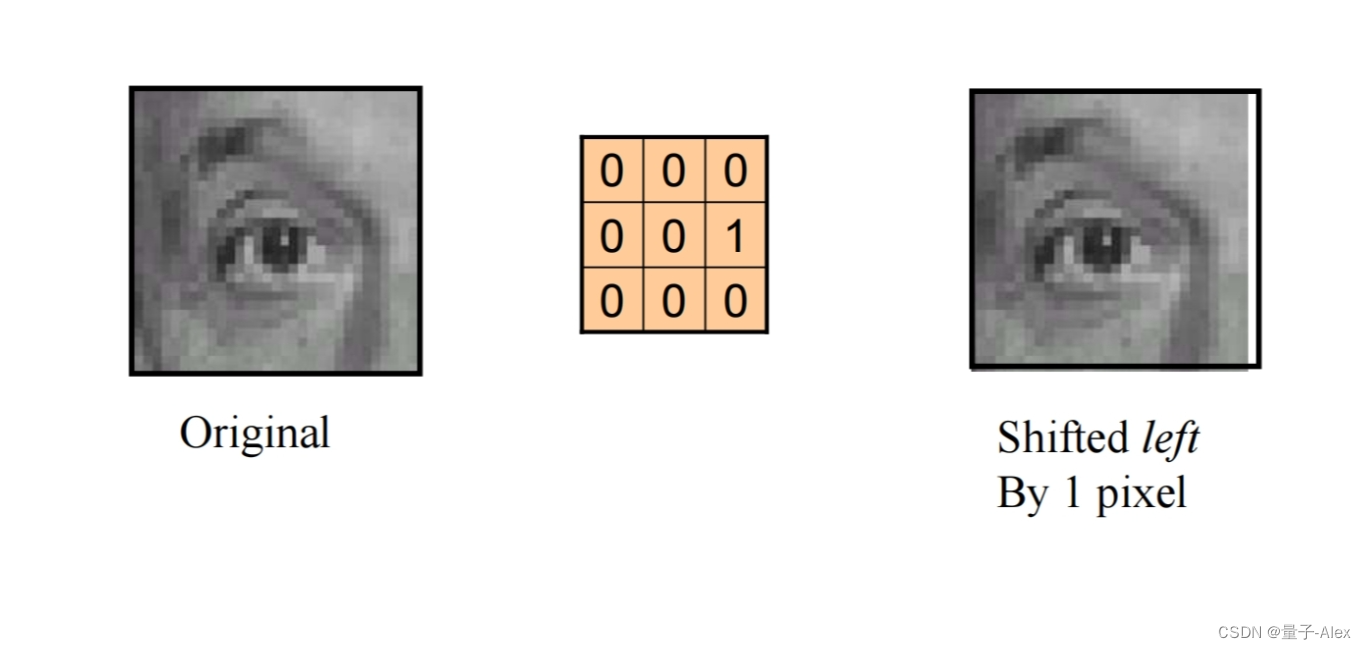
在这里插入图片描述
左移

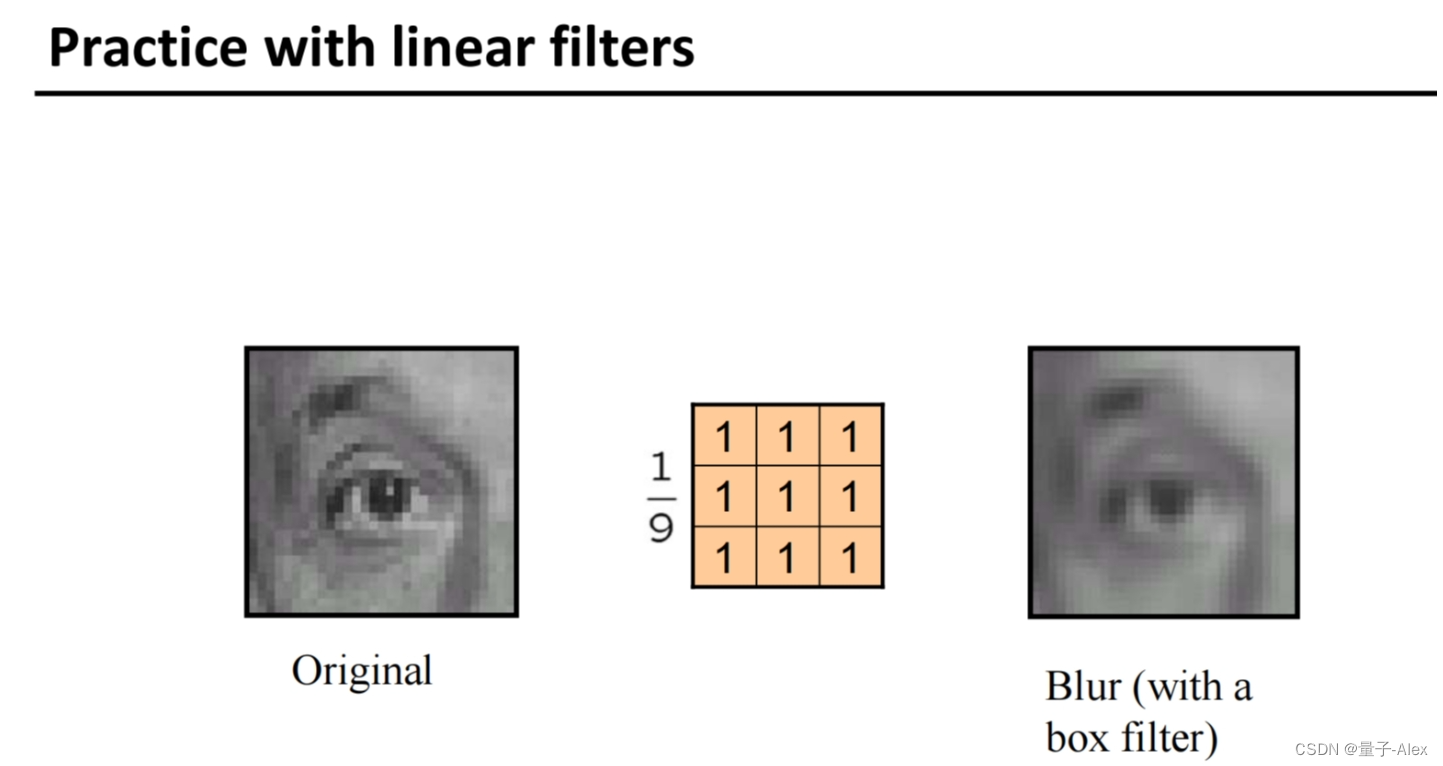
在这里插入图片描述
平滑降噪

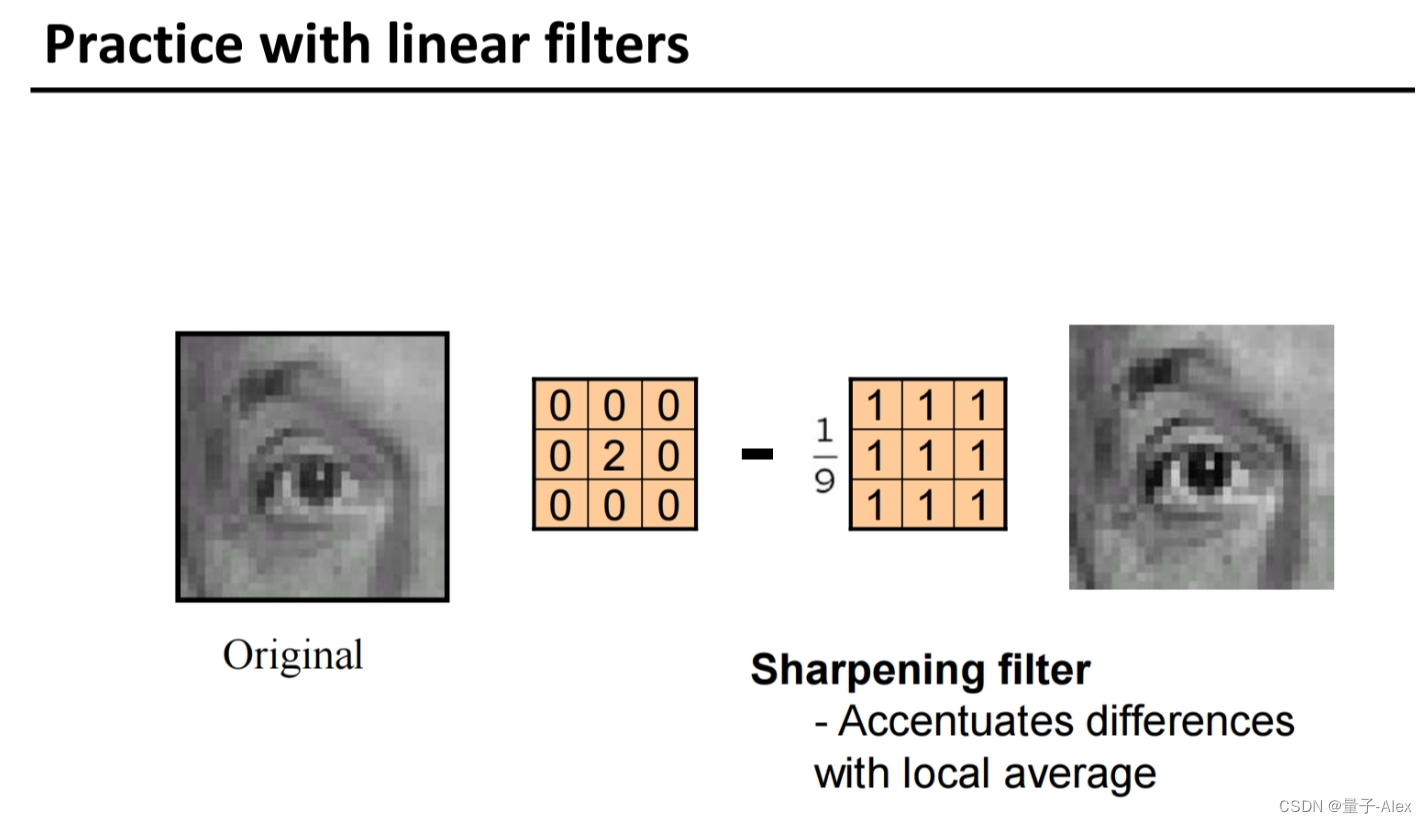
在这里插入图片描述
锐化

7 振铃效应

在这里插入图片描述
在这里插入图片描述
离我近的点权值大、远的点权值小

8 高斯核

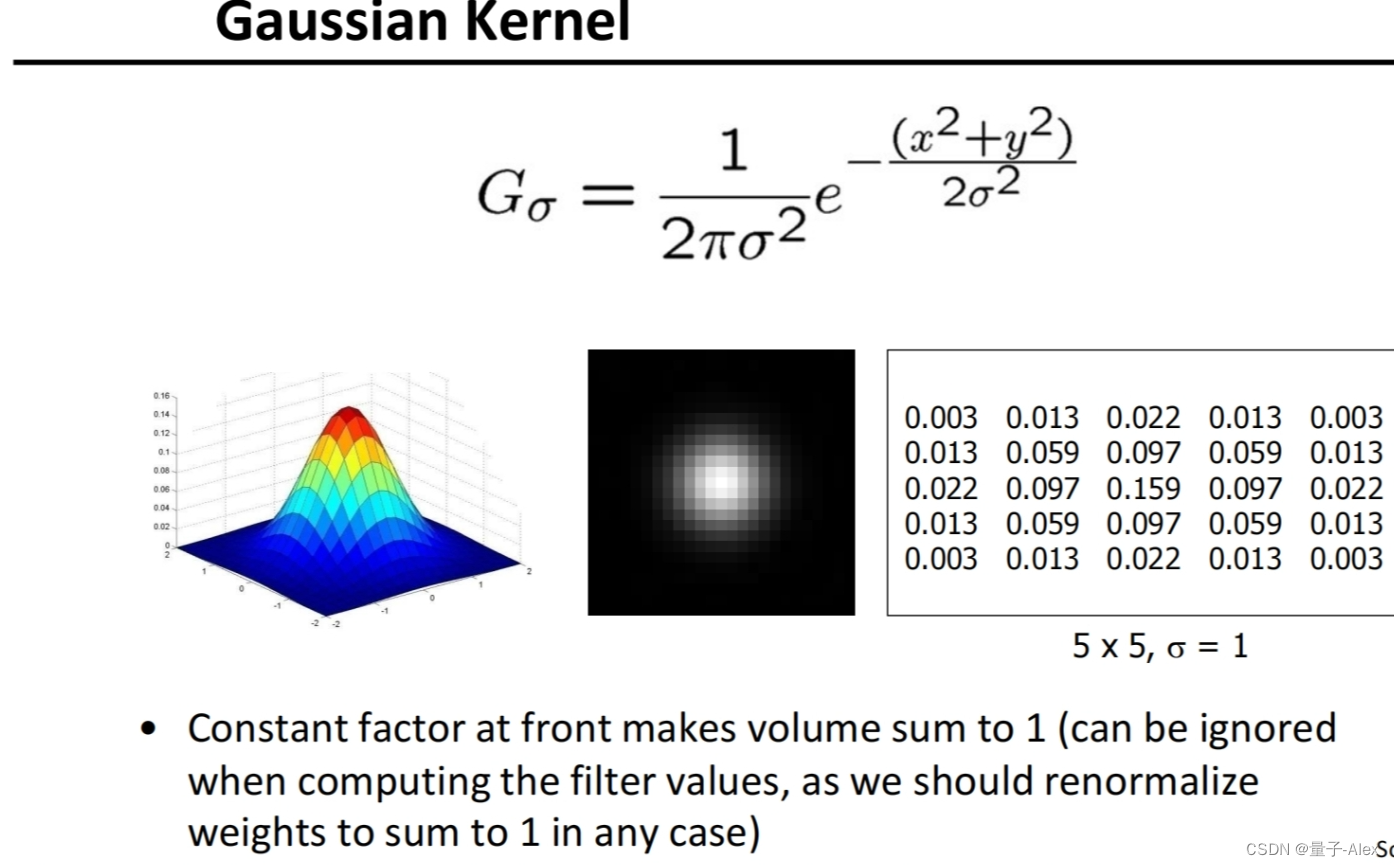
在这里插入图片描述
产生高斯卷积核的步骤：
①指定窗宽
②指定方差 σ \sigma σ
③归一化

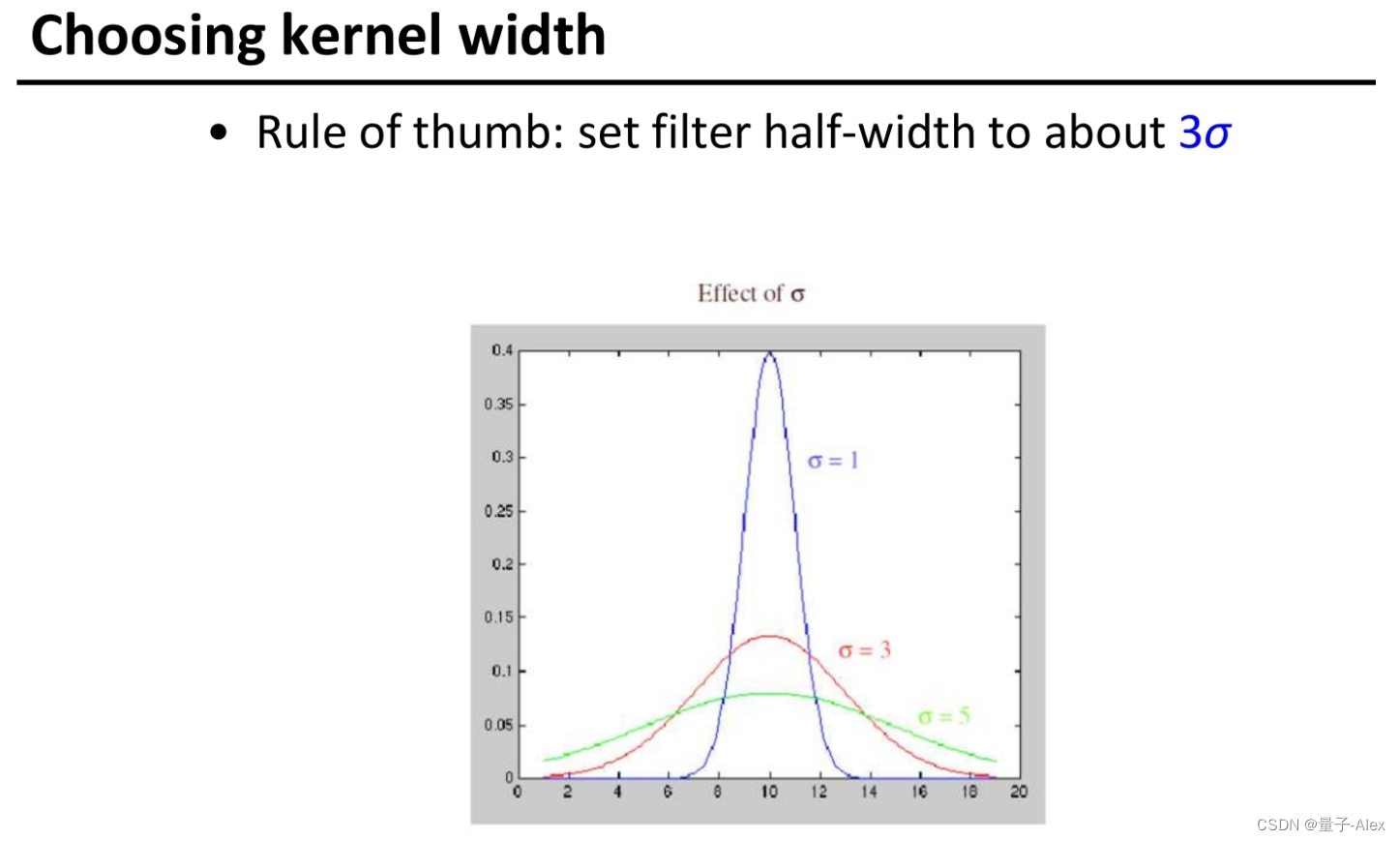
9 高斯核参数

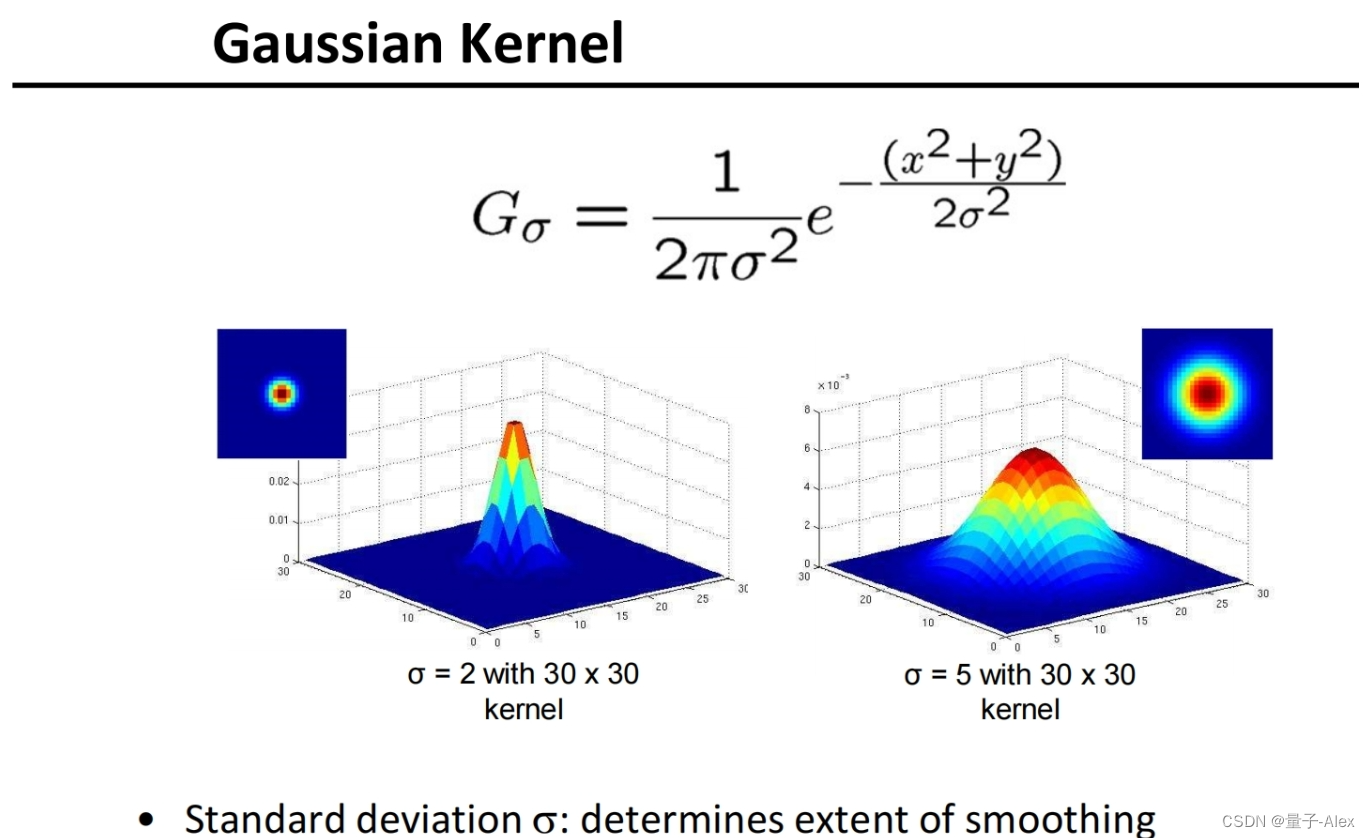
在这里插入图片描述
方差的影响：方差越大，自己的权值占比就越小，平滑的结果越强
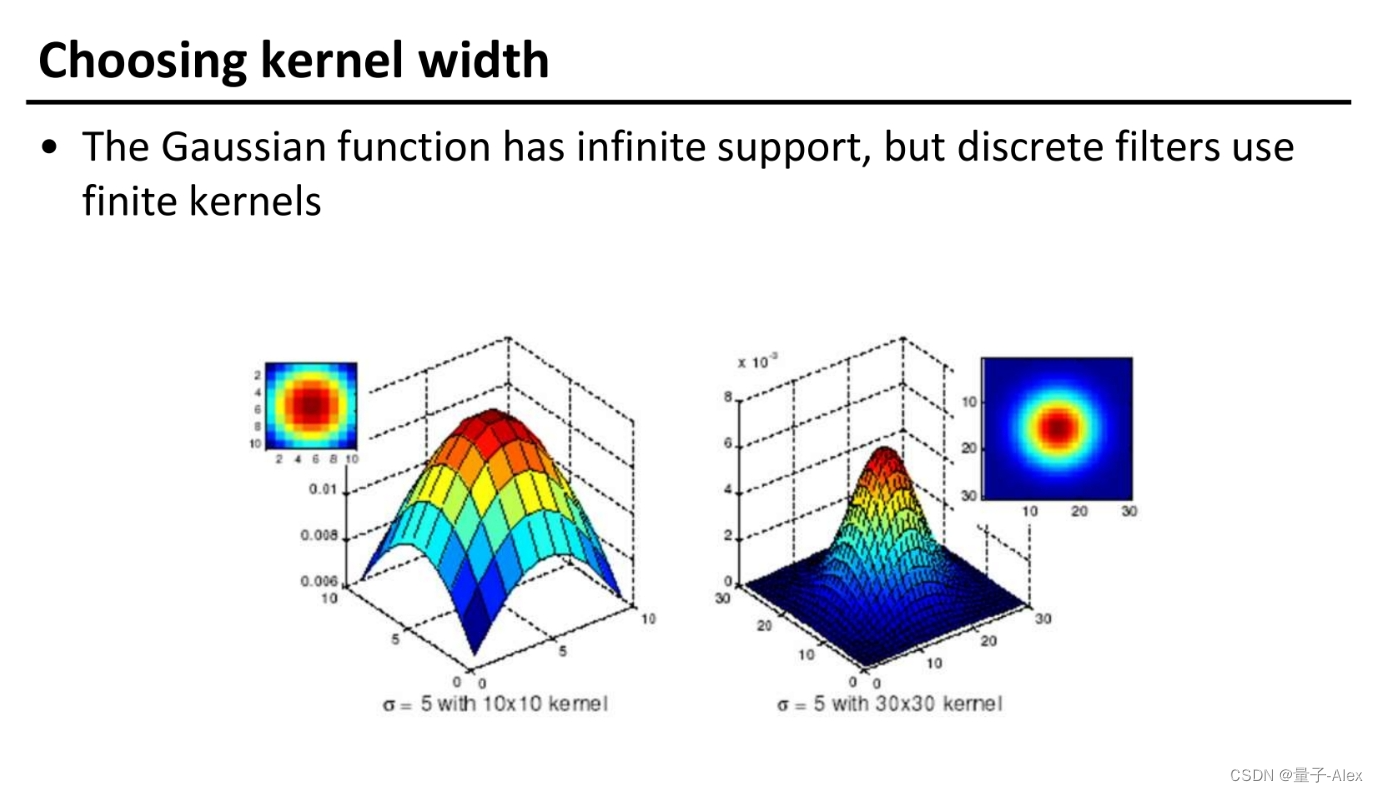在这里插入图片描述方差固定，窗宽越大，归一化计算的分母就大，权值就小，平滑就更厉害

在这里插入图片描述

10 高斯核总结

在这里插入图片描述
滤除高频

一个大高斯核的卷积效果可以由两个小高斯卷积核连续操作得到

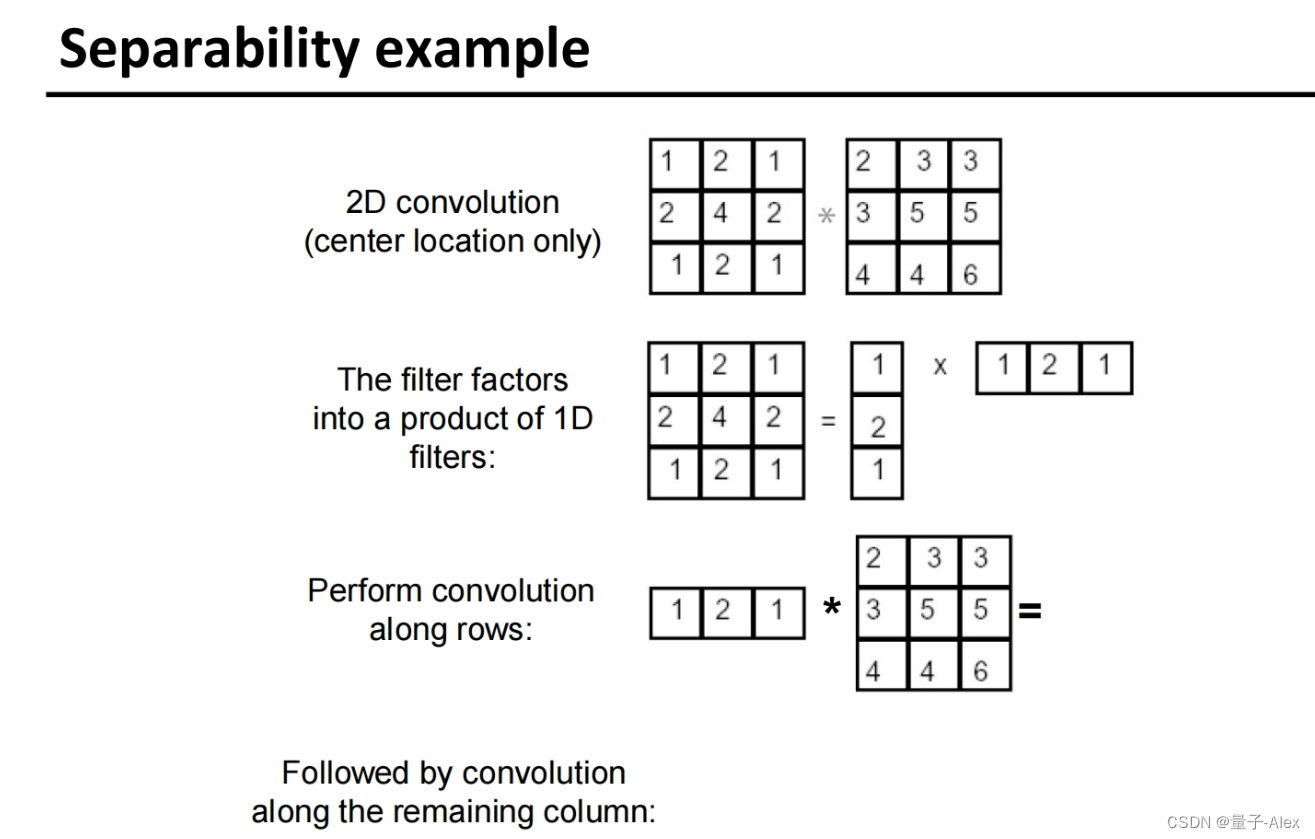
在这里插入图片描述高斯核可以分解

在这里插入图片描述
分解性质有什么作用？
在这里插入图片描述
计算复杂度降低

11 噪声

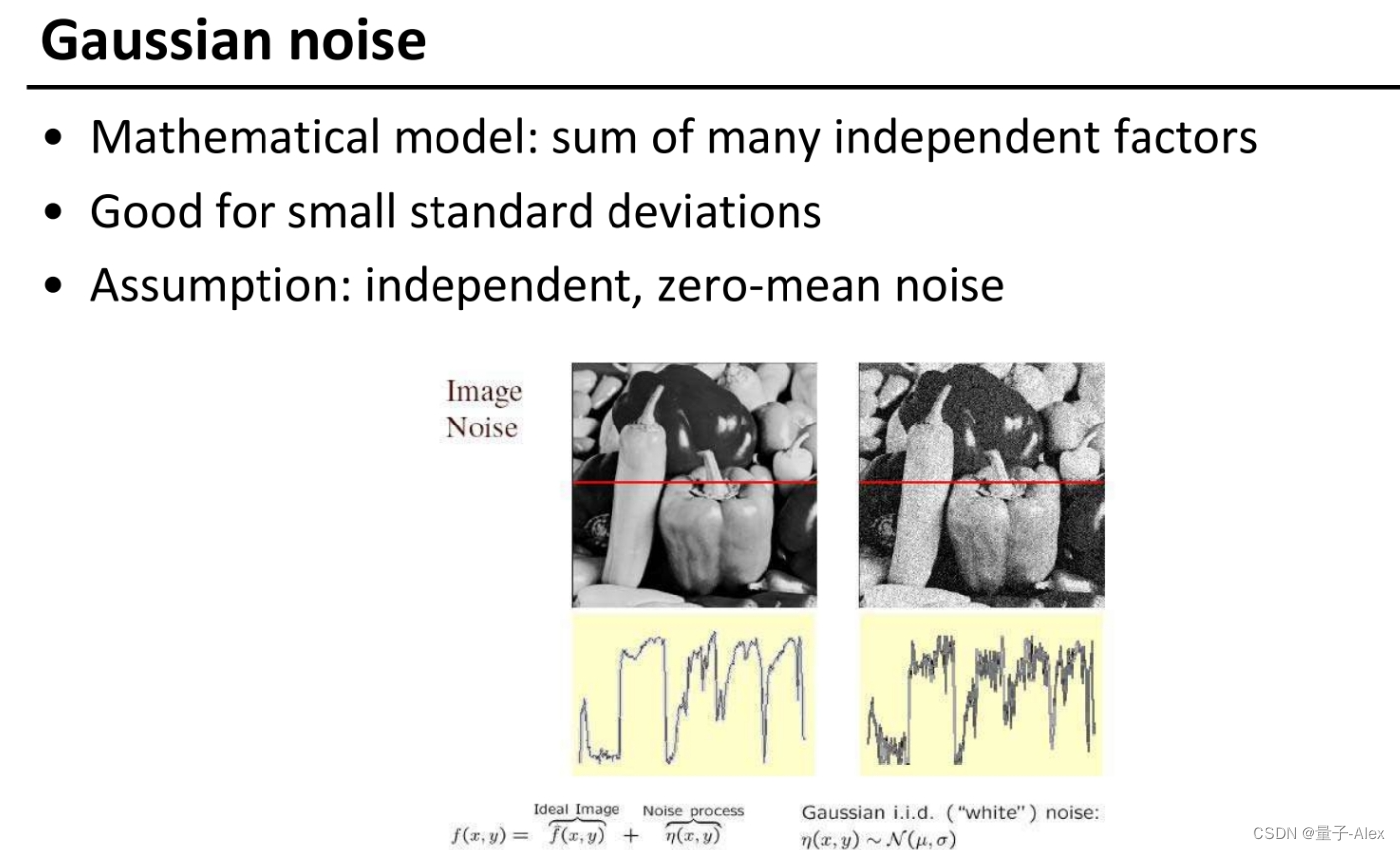
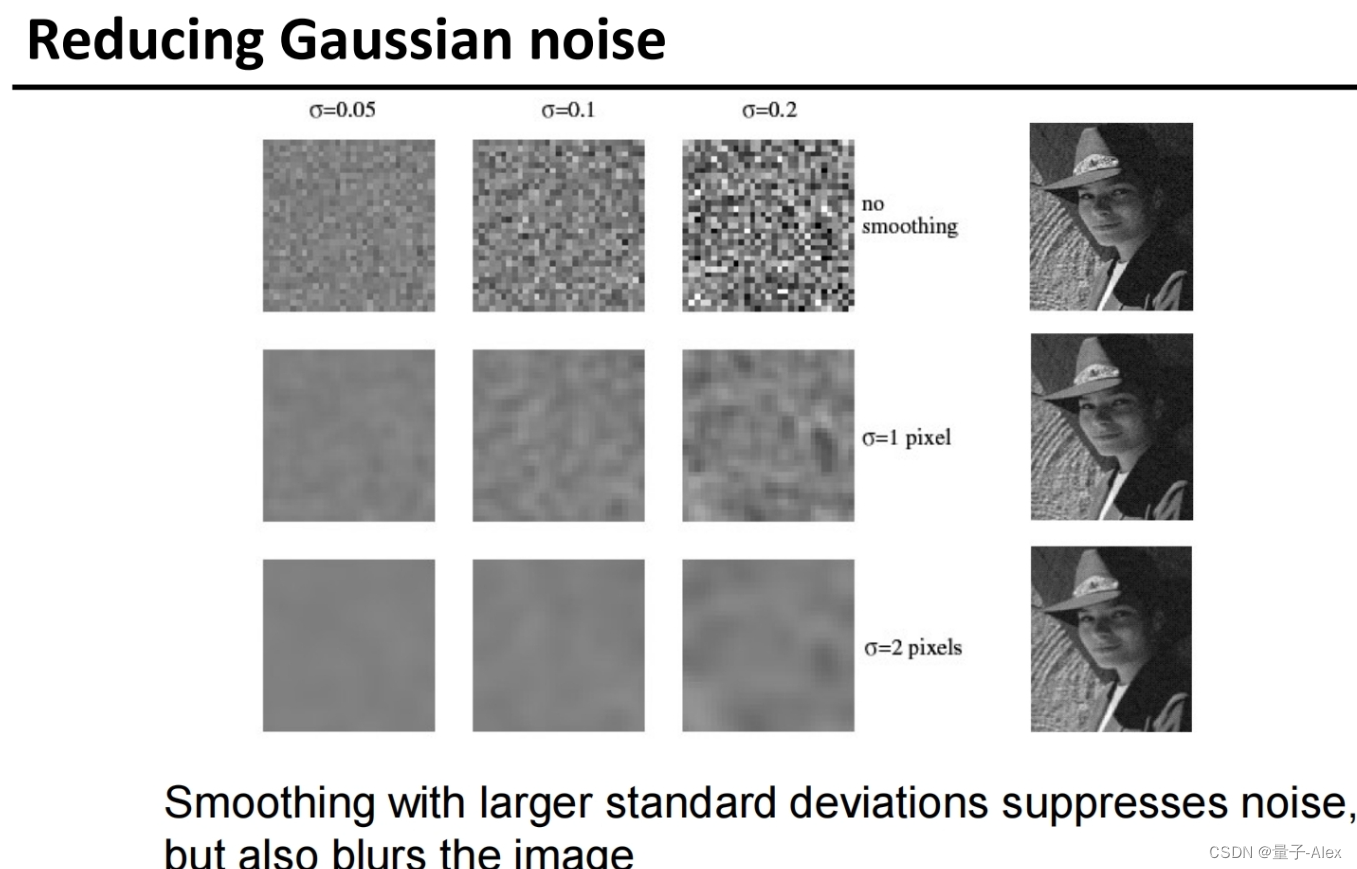
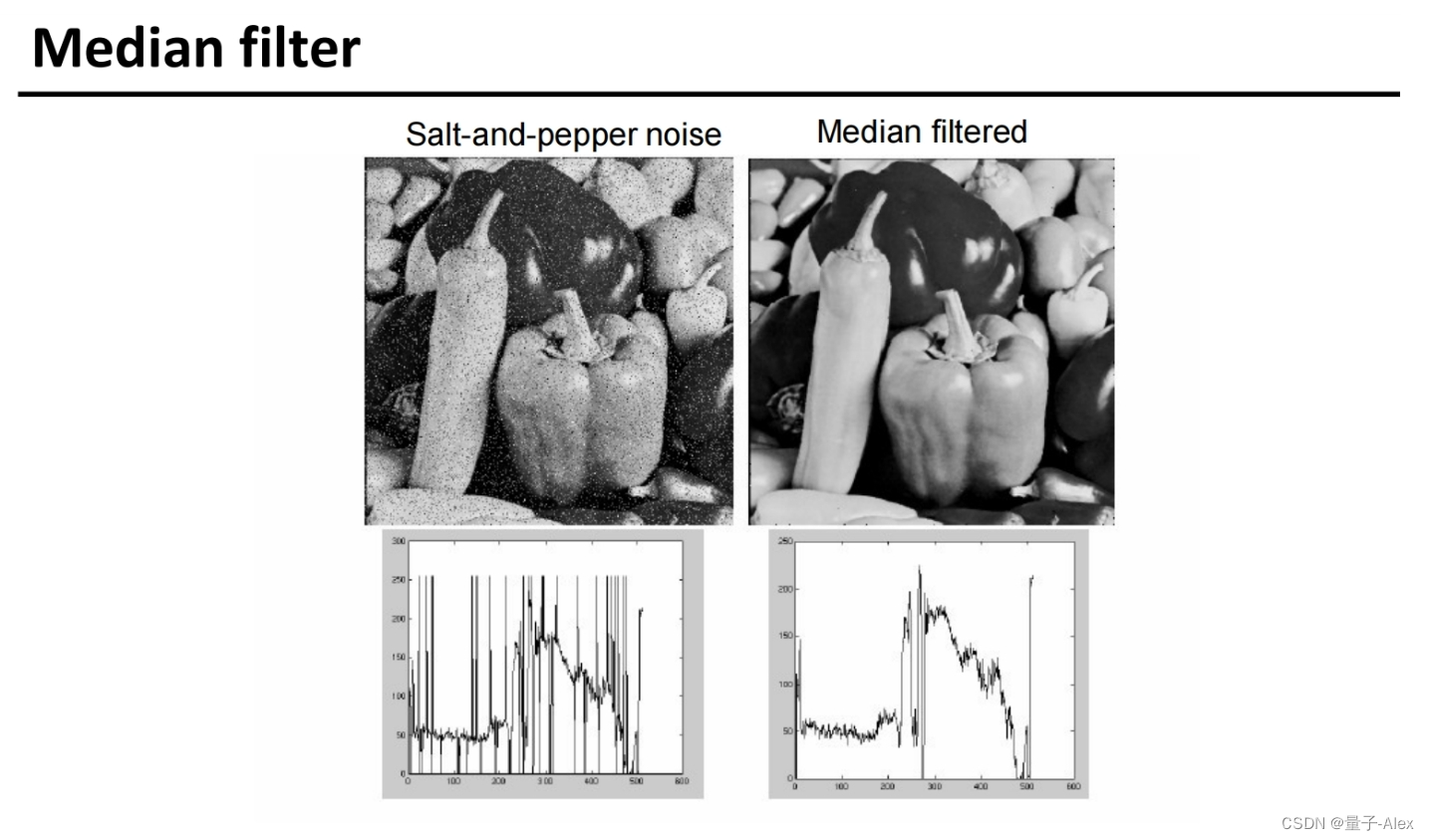
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
高斯滤波对椒盐噪声效果并不好

12 中值滤波

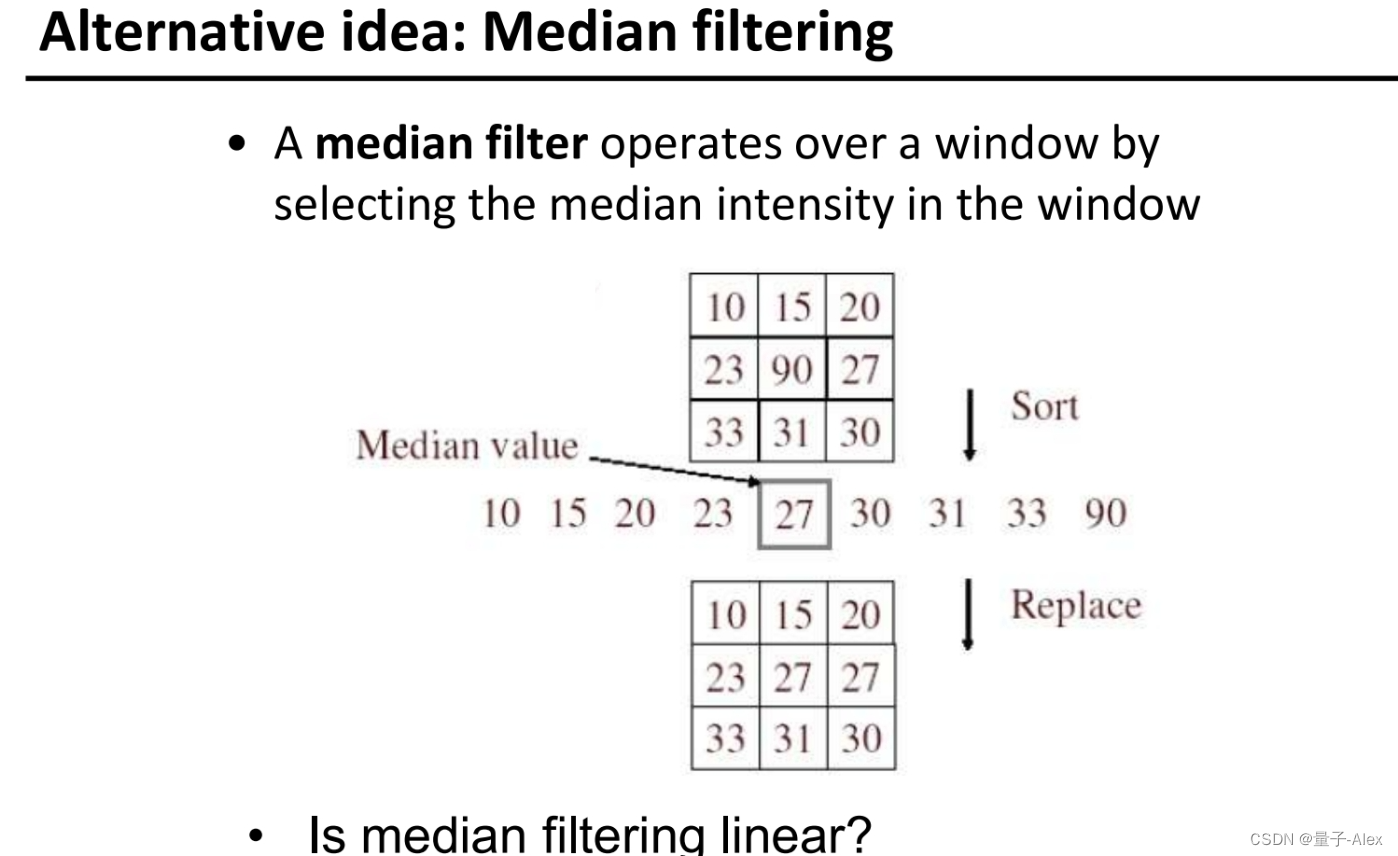
在这里插入图片描述
把这些值从小到大排序，然后选取中值

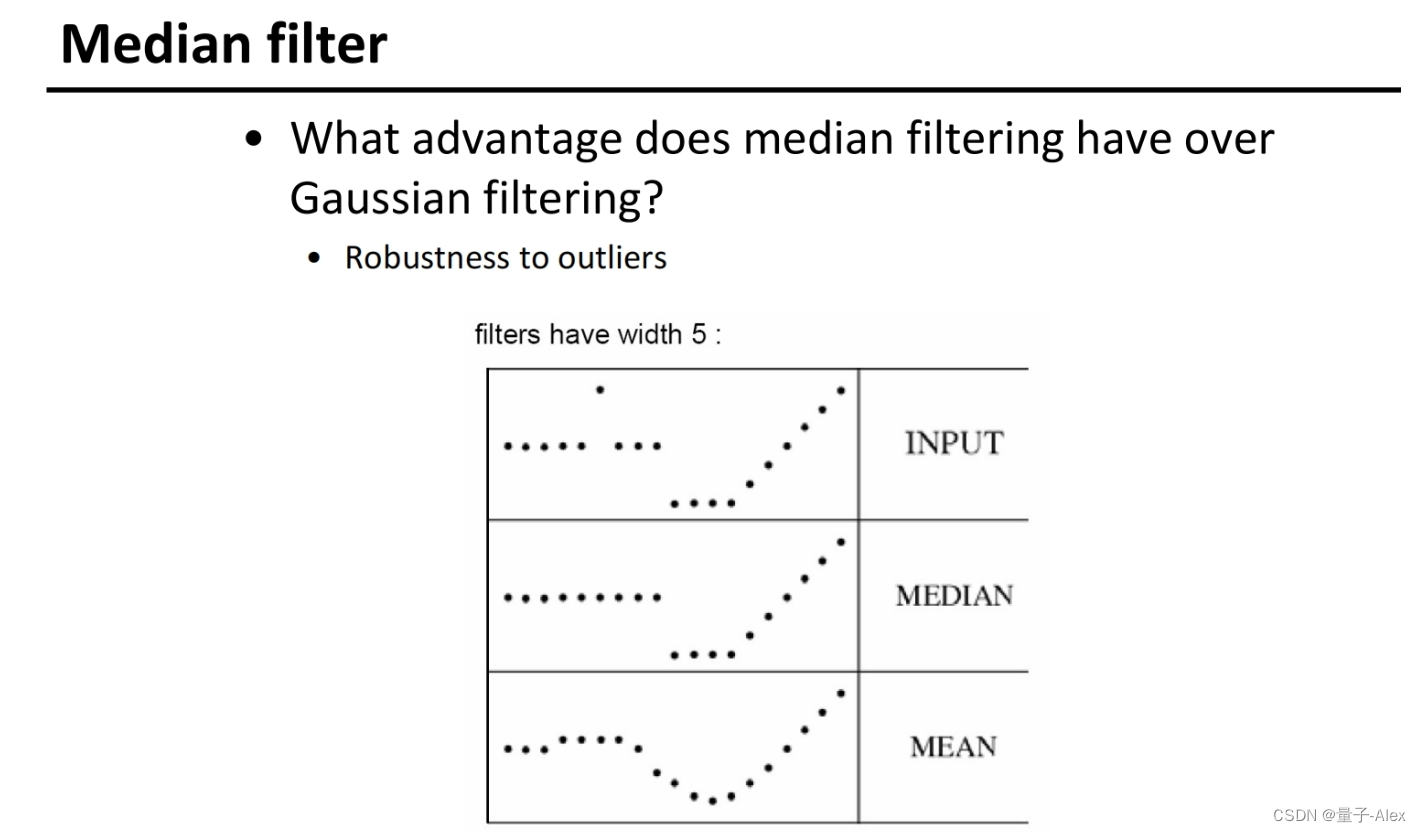
在这里插入图片描述
中值滤波不改变整体形状
在这里插入图片描述

13 拉普拉斯高斯

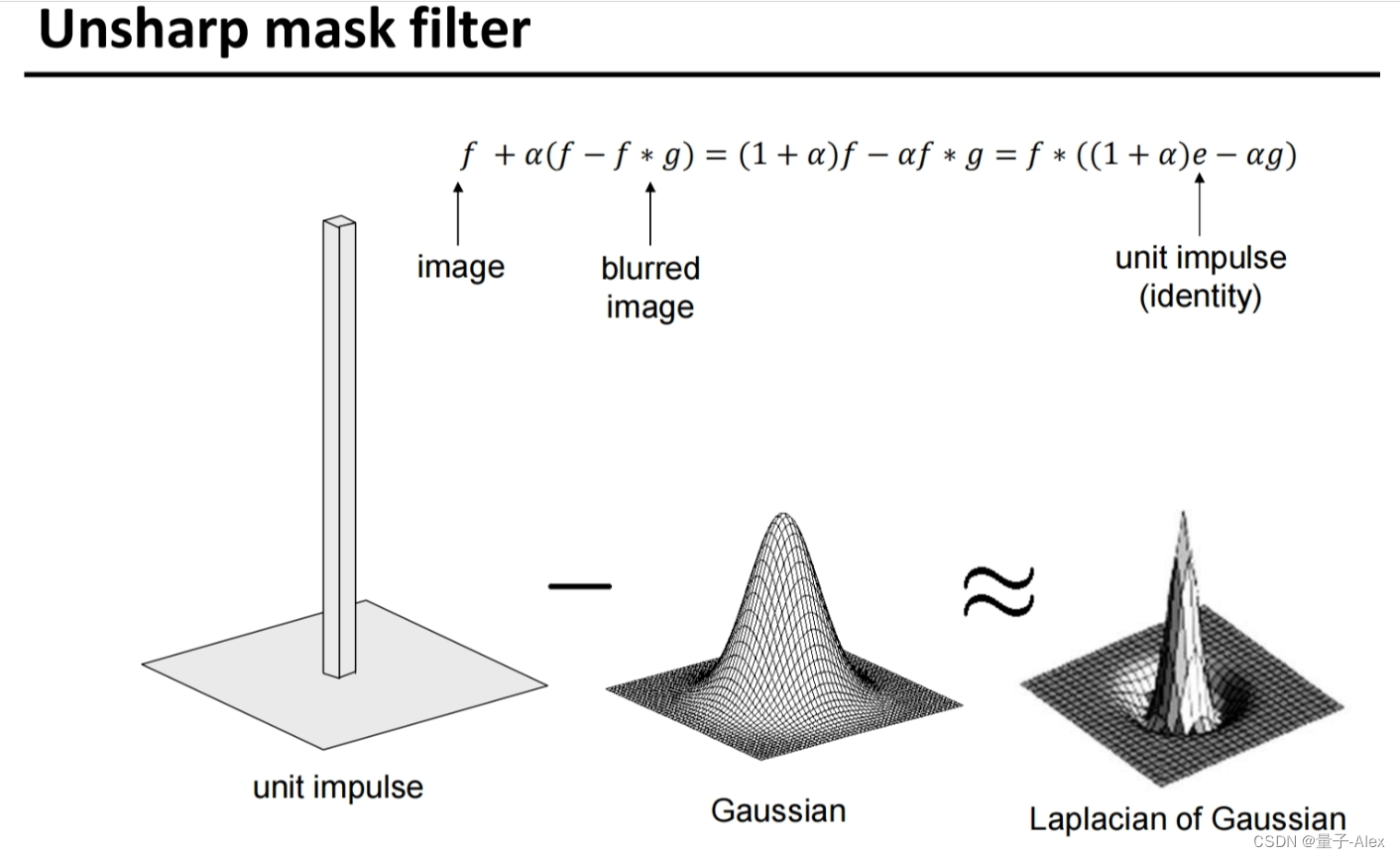
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/677411.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

GPT-4模型的创造力

GPT-4模型的创造力

超级的创造力是GPT-4等高级语言模型的重要特征之一。它们不仅能够精确地模拟和再现各类文本样式、结构和内容，而且在生成新的文本时，能够通过深度学习算法对海量训练数据中捕捉到的模式进行创新性的重组与拓展： 词汇创新：基于已学…
阅读更多...
Redis——集群环境部署

Redis——集群环境部署

一般情况下的Redis，我们都是在一台服务器上进行操作的，也就是说读、写以及备份操作都是在一台Redis服务器上进行的。随着项目访问量的增加，对Redis服务器的操作也更加频繁，虽然Redis读写速度都很快，但是一定程度上也会…
阅读更多...
统一身份认证系统架构设计与实践总结

统一身份认证系统架构设计与实践总结

随着互联网的快速发展和应用的普及，人们在各个网站和应用上需要不同的账号和密码进行身份认证。为了解决这个问题，统一身份认证系统应运而生。本文将总结统一身份认证系统的架构设计与实践经验，帮助读者了解如何设计和实现一个高效、安全的统…
阅读更多...
〖大前端 - ES6篇②〗- let和const

〖大前端 - ES6篇②〗- let和const

说明：该文属于 大前端全栈架构白宝书专栏，目前阶段免费，如需要项目实战或者是体系化资源，文末名片加V！作者：哈哥撩编程，十余年工作经验, 从事过全栈研发、产品经理等工作，目前在公司…
阅读更多...
ORACLE的 软 软 软 解析!

ORACLE的 软 软 软 解析!

在海鲨数据库架构师精英群里,有位朋友说ORACLE 有 软软软解析. 就是把执行计划缓存在客户端里,从而避免去服务端找执行计划. 他给了个设置方法, Weblogic console->datasource->connectionPool Statement Cache Type >LRU Statement Cache Size100 CURSOR_NUMBER …
阅读更多...
求满二叉树两个节点之间的最短距离

求满二叉树两个节点之间的最短距离

求满二叉树两个节点之间的最短距离 using System; using System.Collections.Generic; using System.Linq; using System.Text;namespace FirstSolver {internal class Program{static void Main(string[] args){BinaryTreeNode<int> root1 FullBinaryTree.CreateTree(1…
阅读更多...
python实现基数排序

python实现基数排序

如果在给不同的整形数组排序的时候，一般会这样做，也就是先看最高位，如果最高位数值大的话也就意味着它的数值是最大的，而如果两个数字的最高位的数值是一样的，则继续比较次高位，这样依次去比较可以决定数字的排序。而对于基数排序来说，其思想是与以上的思想是不同的，基…
阅读更多...
Node版本管理 - nvm

Node版本管理 - nvm

简介 nvm 允许用户在同一台电脑上安装并管理多个 Node.js 版本并支持快速切换&#xff0c;对于需要在不同的项目中使用不同版本的 Node.js 的开发者来说非常有用。 使用 下载安装后&#xff0c;以管理员身份打开windows控制台。 # 设置下载node安装包&#xff0c;和npm安装…
阅读更多...
linux系统非关系型数据库redis常见问题以及好处

linux系统非关系型数据库redis常见问题以及好处

redis常见问题以及好处 redis常见问题缓存穿透概念解决方案布隆过滤器缓存空对象 缓存雪崩概念解决方案redis高可用限流降级数据预热 redis好处redis常见性能问题解决方案为redis加密 redis常见问题 缓存穿透 概念 缓存穿透的概念很简单&#xff0c;用户想要查询一个数据&am…
阅读更多...
02-实现方法多值返回-pair与truple

02-实现方法多值返回-pair与truple

在实际的项目开发中&#xff0c;我们经常会遇到返回多个值&#xff0c;通常我们使用Map对象、自定义Class对象等方式封装返回结果。但是这种方式&#xff0c;需要定义大量中间类&#xff0c;影响代码的整体质量。 spring 为我们提供了pair 双值与 triple 三值返回对象。 1、p…
阅读更多...
二级C语言笔试6

二级C语言笔试6

(总分100,考试时间90分钟) 一、选择题 1. 设有以下语句&#xff1a; charx3&#xff0c;y6&#xff0c;z&#xff1b; zx^y&#xff1c;&#xff1c;2&#xff1b; 则z的二进制值是( )。 A. 00010100 B. 00011011 C. 00011100 D. 00011000 …
阅读更多...
从Unity到Three.js（画线组件line）

从Unity到Three.js（画线组件line）

JavaScript 0基础&#xff0c;只是照着官方文档临摹了下&#xff0c;之后有时间再进行细节学习和功能封装。 import * as THREE from three; //引入threejsconst renderer new THREE.WebGLRenderer();//创建渲染器 //设置渲染范围&#xff0c;当前撑满全屏,屏幕左上角是&…
阅读更多...
C++类型转化cast from pointer to smaller type ‘int‘ loses information

C++类型转化cast from pointer to smaller type ‘int‘ loses information

代码如下 #include <iostream>int main() {int a 10;std::cout << (int)&a << std::endl;return 0; }编译 这段代码是要将地址转化成整数类型&#xff0c;但是在编译时编译器告诉我们这是错的&#xff0c;因为在C中&#xff0c;将指针转换为int类型的…
阅读更多...
Spring IoC容器详解

Spring IoC容器详解

版权声明 本文原创作者&#xff1a;谷哥的小弟作者博客地址&#xff1a;http://blog.csdn.net/lfdfhl 基本概念 Spring IoC容器是Spring框架的核心组件&#xff0c;它实现了控制反转&#xff08;Inversion of Control&#xff0c;IoC&#xff09;的设计原则。IoC是一种编程思…
阅读更多...
【前端高频面试题--TypeScript篇】

【前端高频面试题--TypeScript篇】

&#x1f680; 作者 &#xff1a;“码上有前” &#x1f680; 文章简介 &#xff1a;前端高频面试题 &#x1f680; 欢迎小伙伴们 点赞&#x1f44d;、收藏⭐、留言&#x1f4ac; 高频前端面试题--Vue3.0篇 什么是TypeScript&#xff1f;TypeScript数据类型TypeScript中命名空…
阅读更多...
最关键的十个图像特征

最关键的十个图像特征

在计算机视觉中&#xff0c;图像特征是用来描述图像中视觉元素的一组属性&#xff0c;它们对于图像识别、分类、检测和分割等任务至关重要。以下是10个在计算机视觉中广泛使用的最重要的图像特征&#xff1a; 颜色直方图&#xff08;Color Histogram&#xff09;&#xff1a; 颜…
阅读更多...
Days 27 ElfBoard 板 AltiumDesigner 相同电路快速布局布线

Days 27 ElfBoard 板 AltiumDesigner 相同电路快速布局布线

在进行设计开发的时候&#xff0c;总会遇到相同的电路&#xff0c;或者模块&#xff0c;这些电路可以使用相同的布局和走线&#xff0c;例如 DC-DC 电源、网口 PHY 电路部分。这类型的电路&#xff0c;我们可以采用AltiumDesigner 中的 Room 进行布局和布线的快速复制&#xff…
阅读更多...
C#系列-并行处理+异步流（5）

C#系列-并行处理+异步流（5）

一&#xff0c;C#并行处理 在C#中&#xff0c;并行处理指的是同时执行多个任务或操作&#xff0c;以利用多核或多处理器的优势&#xff0c;从而提高应用程序的性能。C#提供了多种工具和框架来帮助开发者实现并行处理。以下是一些在C#中实现并行处理的方法&#xff1a; Paralle…
阅读更多...
VitePress-12-markdown中使用vue的语法

VitePress-12-markdown中使用vue的语法

前言 VitePress 中&#xff0c;markdown文档最终都会转换成为 html文件&#xff0c;我们在访问的时候&#xff0c;也是直接访问的 xxx.html 文件。而且&#xff0c;markdown文档会被作为 [vue单文件] 进行处理&#xff0c;因此&#xff0c;我们我们可以在文档中使用 vue 语法&…
阅读更多...
决策树之scikit-learn

决策树之scikit-learn

实例 from sklearn.datasets import load_iris from sklearn import tree import matplotlib.pyplot as plt# Load iris dataset iris load_iris() X, y iris.data, iris.target# Fit the classifier clf tree.DecisionTreeClassifier() clf clf.fit(X, y)# Plot the deci…
阅读更多...
最新文章

Copyright @ 2022~2023