政安晨：示例演绎机器学习中（深度学习）神经网络的数学基础——快速理解核心概念（二）{两篇文章讲清楚}

这一篇与上一篇是兄弟篇，意在通过两篇文章讲清楚深度学习中神经网络的数学基础，第一次看到这篇文章的小伙伴可以从上一篇文章看起（包括搭建环境等等都在上一篇），上一篇链接如下：

政安晨：示例演绎机器学习中（深度学习）神经网络的数学基础——快速理解核心概念（一）{两篇文章讲清楚}https://blog.csdn.net/snowdenkeke/article/details/136089968

张量运算

如果把人工智能领域比作星辰大海，那么机器学习就是渡海之舟，而神经网络就是这舟中的机器，

咱们这篇文章要介绍的张量运算，就是这架机器中的齿轮！这是基础的基础，也是核心的核心！

计算机程序最终都可以简化为对二进制输入的一些二进制运算（AND、OR、NOR等），与此类似，深度神经网络学到的所有变换也都可以简化为对数值数据张量的一些张量运算（tensor operation）或张量函数（tensor function），如张量加法、张量乘法等。

我以前做过一个例子，请见下面这篇文章：

政安晨的机器学习笔记——基于Anaconda安装TensorFlow并尝试一个神经网络小实例https://blog.csdn.net/snowdenkeke/article/details/135841281在我以前的这个例子里，最后部分尝试了一个神经网络小实例，里面涉及了通过叠加Dense层来构建模型。

keras.layers.Dense(512, activation="relu")

你可以将这个层理解为一个函数，其输入是一个矩阵，返回的是另一个矩阵，即输入张量的新表示。

就像下面这个函数：

output = relu(dot(input, W) + b)

（其中W是一个矩阵，b是一个向量，二者都是该层的属性）。

我们将上式拆开来看：这里有3个张量运算，输入张量和张量W之间的点积运算（dot），由此得到的矩阵与向量b之间的加法运算（+）。

relu运算：relu(x)就是max(x, 0)，relu代表“修正线性单元”（rectified linear unit）。

虽然咱们讲的是数学和算法，但咱们确是始终记得咱们的目标是演绎，程序的事交给程序，用程序来演绎数学和算法是咱们做程序员的下意识行为，呵呵。

逐元素运算

relu运算和加法都是逐元素（element-wise）运算，即该运算分别应用于张量的每个元素。

也就是说，这些运算非常适合大规模并行实现，如果你想对逐元素运算编写一个简单的Python实现，那么可以使用for循环。

下列代码是对逐元素relu运算的简单实现：

def naive_relu(x):#x是一个2阶NumPy张量assert len(x.shape) == 2#避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] = max(x[i, j], 0)return x

对于加法，可采用同样的实现方法：

def naive_add(x, y):#x和y是2阶NumPy张量assert len(x.shape) == 2assert x.shape == y.shape#避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] += y[i, j]return x

利用同样的方法，可以实现逐元素的乘法、减法等。

在实践中处理NumPy数组时，这些运算都是优化好的NumPy内置函数，这些函数将大量运算交给基础线性代数程序集（Basic Linear Algebra Subprograms，BLAS）实现，BLAS是低层次（low-level）、高度并行、高效的张量操作程序，通常用Fortran或C语言来实现。

在NumPy中可以直接进行下列逐元素运算，速度非常快。

import numpy as np# 逐元素加法
z = x + y# 逐元素relu
z = np.maximum(z, 0.)

我们来看一下两种方法运行时间的差别：

方式一 ——> Numpy优化的：

import timex = np.random.random((20, 100))
y = np.random.random((20, 100))
t0 = time.time()
for _ in range(1000):z = x + yz = np.maximum(z, 0.)
print("Took: {0:.2f} s".format(time.time() - t0))

（这一种运行方式就是被NumPy优化好的{内置函数}（这还是在我的CPU版本的笔记本电脑上运行的））

方式二 ——>咱们现场手工实现的滴:

def naive_add(x, y):#x和y是2阶NumPy张量assert len(x.shape) == 2assert x.shape == y.shape#避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] += y[i, j]return xdef naive_relu(x):#x是一个2阶NumPy张量assert len(x.shape) == 2#避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] = max(x[i, j], 0)return xt0 = time.time()
for _ in range(1000):z = naive_add(x, y)z = naive_relu(z)
print("Took: {0:.2f} s".format(time.time() - t0))

小伙伴们看到了吧，咱们临时实现的函数对同样的运算，花了2.75秒，是刚才第一种方法0.01秒的275倍！

另外，如果在GPU上运行TensorFlow或者PyTorch代码，逐元素运算都是通过完全向量化的CUDA来完成的，可以最大限度地利用高度并行的GPU芯片架构。

广播

刚才咱们对naive_add的简单实现仅支持两个形状相同的2阶张量相加，但在我文章前面介绍的Dense层中，我们将一个2阶张量与一个向量相加。如果将两个形状不同的张量相加，会发生什么？在没有歧义且可行的情况下，较小的张量会被广播（broadcast），以匹配较大张量的形状。广播包含以下两步：

A . 向较小张量添加轴[叫作广播轴（broadcast axis）]，使其ndim与较大张量相同。

B . 将较小张量沿着新轴重复，使其形状与较大张量相同。

举例来说（x的形状是(32, 10)，y的形状是(10,)）：

import numpy as np# x是一个形状为(32, 10)的随机矩阵
x = np.random.random((32, 10))# y是一个形状为(10,)的随机向量
y = np.random.random((10,))

咱们可以像这样查看一下x 与 y的值分别是什么（我是在本地环境的Jupyter Notebook中运行的）？

上面这个张量，是一个32行10列的二阶张量（也就是32×10的二阶矩阵）

上面这个是一个向量（咱们姑且可以称为一阶张量）（其实就是10个元素的数组）。

把它俩进行运算的过程是这样滴：

1. 首先，我们向y添加第1个轴（空的），这样y的形状变为(1, 10):

# 现在y的形状变为(1, 10)
y = np.expand_dims(y, axis=0)

您会看到此时y的值为：

注意：上面这里已经是2个中括号哦！

2. 然后，我们将y沿着这个新轴重复32次，这样得到的张量Y的形状为(32, 10)，并且Y[i, :] == y for i in range(0, 32):

# 将y沿着轴0重复32次后得到Y，其形状为(32, 10)
y = np.concatenate([y] * 32, axis=0)

此时，您会看到y被复制了32次：

3. 现在，我们可以将X和Y相加，因为它们的形状相同啦。

当然，在实际的实现过程中并不会创建新的2阶张量，因为那样做非常低效。重复操作完全是虚拟的，它只出现在算法中，而没有出现在内存中。但想象将向量沿着新轴重复10次，是一种很有用的思维模型。

下面是一种简单实现：

def naive_add_matrix_and_vector(x, y):# x是一个2阶NumPy张量assert len(x.shape) == 2# y是一个NumPy向量assert len(y.shape) == 1  assert x.shape[1] == y.shape[0]# 避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] += y[j]return x

如果一个张量的形状是(a, b, ..., n, n+1, ..., m)，另一个张量的形状是(n, n+1, ..., m)，那么通常可以利用广播对这两个张量做逐元素运算。广播会自动应用于从a到n-1的轴。

下面这个例子利用广播对两个形状不同的张量做逐元素maximum运算：

import numpy as np# x是一个形状为(64, 3, 32, 10)的随机张量
x = np.random.random((64, 3, 32, 10))# y是一个形状为(32, 10)的随机张量
y = np.random.random((32, 10))# 输出z的形状为(64, 3, 32, 10)，与x相同
z = np.maximum(x, y)

咱们来看上面这段代码，x随机了一个4阶张量：

y随机了一个2阶张量：

z为张量的Numpy运算：

咱们看一下z的形状：

这个形状与x是一样的。

张量积

张量积（tensor product）或点积（dot product）是最常见且最有用的张量运算之一。

注意，不要将其与逐元素乘积（*运算符）弄混，在NumPy中，使用np.dot函数来实现张量积，因为张量积的数学符号通常是一个点（dot）。

下面为点积运算的代码：

x = np.random.random((32,))
y = np.random.random((32,))
z = np.dot(x, y)

数学符号中的点（•）表示点积运算。

z = x•y

咱们可以看到x和y的值：

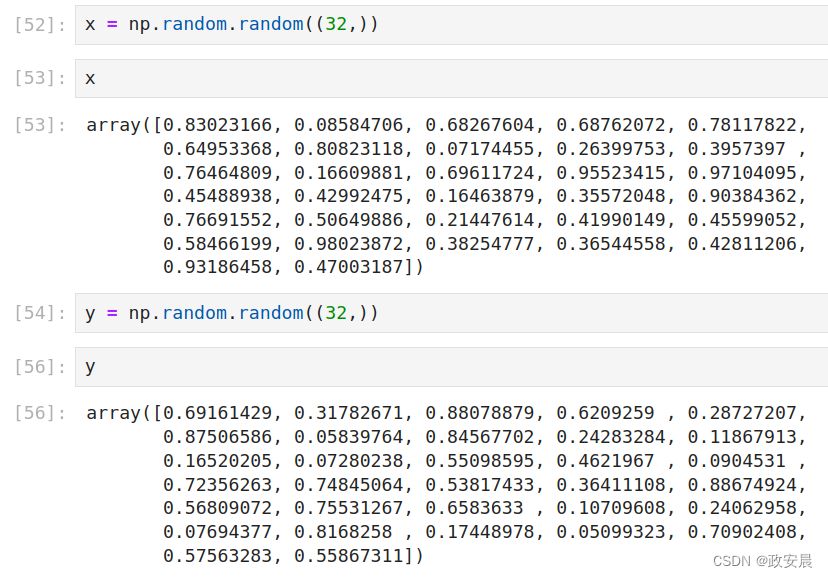
接下来，咱们可以看到点积的计算：z = np.dot(x, y)

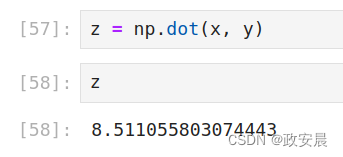
小伙伴们看到了吧，两个向量的点积是一个值（也就是一个标量）。

从数学角度来看，点积运算做了什么？

我们再看一下两个向量x和y的点积的计算过程：

def naive_vector_dot(x, y):# (本行及以下1行) x和y都是NumPy向量assert len(x.shape) == 1assert len(y.shape) == 1assert x.shape[0] == y.shape[0]z = 0.for i in range(x.shape[0]):z += x[i] * y[i]return z

可以看到，两个向量的点积是一个标量，而且只有元素个数相同的向量才能进行点积运算。

你还可以对一个矩阵x和一个向量y做点积运算，其返回值是一个向量，其中每个元素是y和x每一行的点积，实现过程如下：

def naive_matrix_vector_dot(x, y):# x是一个NumPy矩阵assert len(x.shape) == 2# y是一个NumPy向量assert len(y.shape) == 1# x的第1维与y的第0维必须大小相同！assert x.shape[1] == y.shape[0]z = np.zeros(x.shape[0])# 这个运算返回一个零向量，其形状与x.shape[0]相同for i in range(x.shape[0]):for j in range(x.shape[1]):z[i] += x[i, j] * y[j]return z

你还可以重复使用前面写过的代码，从中可以看出矩阵−向量点积与向量−向量点积之间的关系：

def naive_matrix_vector_dot(x, y):z = np.zeros(x.shape[0])for i in range(x.shape[0]):z[i] = naive_vector_dot(x[i, :], y)return z

注意：

只要两个张量中有一个的ndim大于1，dot运算就不再是对称（symmetric）的，也就是说，dot(x, y)不等于dot(y, x)。

当然，点积可以推广到具有任意轴数的张量，最常见的应用可能是两个矩阵的点积。

对于矩阵x和y，当且仅当x.shape[1] == y.shape[0]时，你才可以计算它们的点积（dot(x, y)），点积结果是一个形状为(x.shape[0],y.shape[1])的矩阵，其元素是x的行与y的列之间的向量点积，简单实现如下：

def naive_matrix_dot(x, y):# (本行及以下1行) x和y都是NumPy矩阵assert len(x.shape) == 2assert len(y.shape) == 2# x的第1维与y的第0维必须大小相同！assert x.shape[1] == y.shape[0]# 这个运算返回一个特定形状的零矩阵z = np.zeros((x.shape[0], y.shape[1]))# 遍历x的所有行……for i in range(x.shape[0]):# ……然后遍历y的所有列for j in range(y.shape[1]):row_x = x[i, :]column_y = y[:, j]z[i, j] = naive_vector_dot(row_x, column_y)return z

为了便于理解点积的形状匹配，可以将输入张量和输出张量像下图那样排列，利用可视化来帮助理解。在下图中，x、y和z都用矩形表示（元素按矩形排列）。

由于x的行和y的列必须具有相同的元素个数，因此x的宽度一定等于y的高度。如果你打算开发新的机器学习算法，可能经常要画这种图。

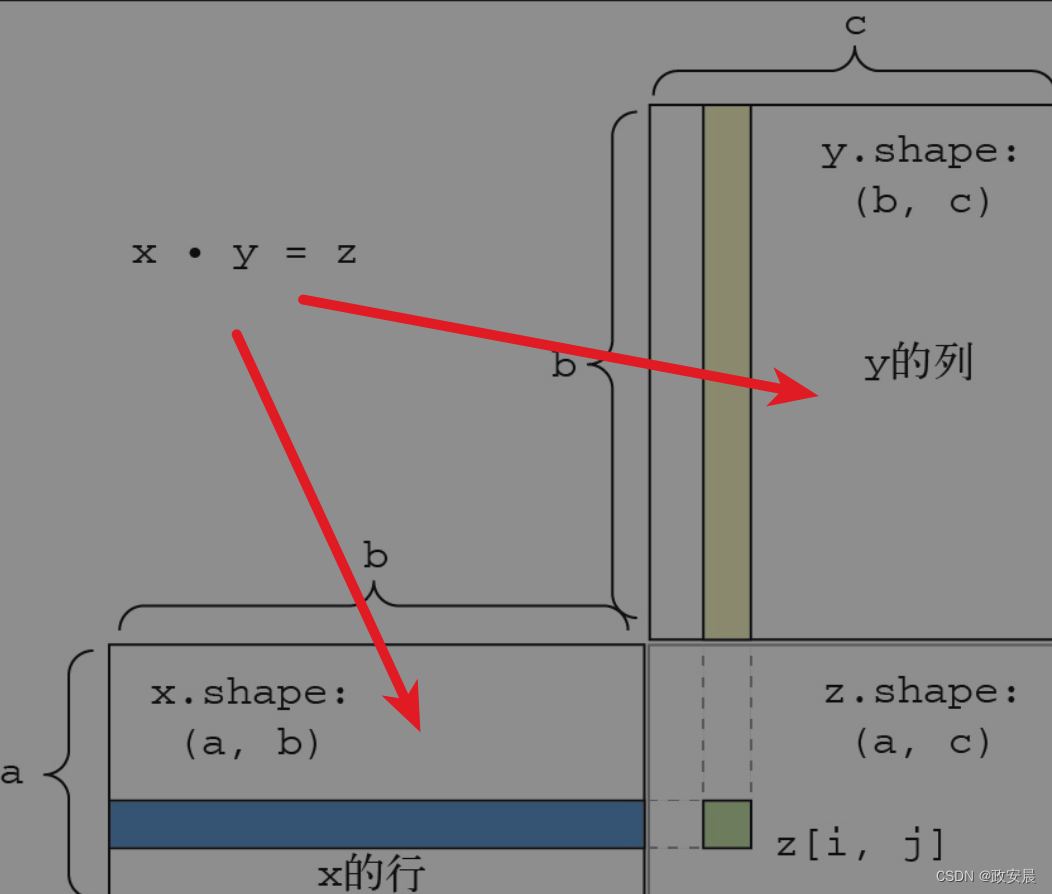
更一般地说，可以对更高阶的张量做点积运算，只要其形状匹配遵循与前面2阶张量相同的原则。

(a, b, c, d)•(d,)→(a, b, c)

(a, b, c, d)•(d, e)→(a, b, c, e)

张量变形

另一个需要了解的张量运算是张量变形（tensor reshaping）。

虽然我刚讲的神经网络例子的Dense层中没有用到它，但将数据输入神经网络之前，可能在预处理数据时将到了这种运算。

train_images = train_images.reshape((60000, 28 * 28))

张量变形是指重新排列张量的行和列，以得到想要的形状，变形后，张量的元素个数与初始张量相同。

下面这个简单的例子可以帮助我们理解张量变形：

咱们定义一个2阶张量：

x = np.array([[0., 1.], [2., 3.], [4., 5.]])

咱们看一下x的形状：

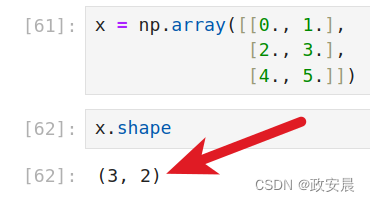
咱们将x进行张量变形：

x = x.reshape((6, 1))

咱们将x再变形：

 x = x.reshape((2, 3))

常见的一种特殊的张量变形是转置（transpose），矩阵转置是指将矩阵的行和列互换，即把x[i, :]变为x[:, i]。

>>>   ←----
>>> 
>>> x.shape
(20, 300)

咱们将创建一个形状为(300, 20)的零矩阵：

x = np.zeros((300, 20))

已经创建的矩阵如下：

这个矩阵的形状，现在是：(300，20)

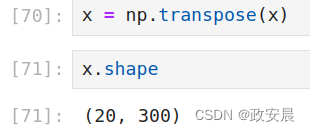
咱们现在对x进行矩阵的转置操作：

x = np.transpose(x)

转置后的形状为（20, 300），如下：

张量运算的几何解释

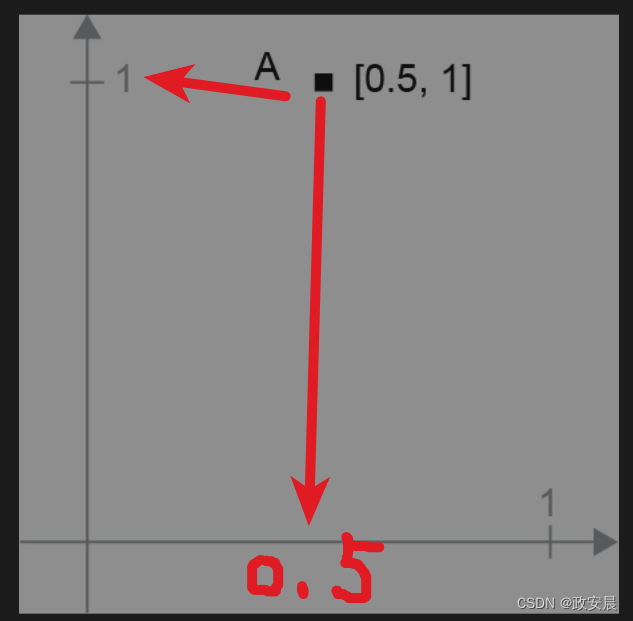
对于张量运算所操作的张量，其元素可看作某个几何空间中的点的坐标，因此所有的张量运算都有几何解释。以加法为例，假设有这样一个向量：

A = [0.5, 1]

它是二维空间中的一个点（见下图）：

咱们在张量运算中的常见做法是将向量描绘成由原点指向这个点的箭头。

假设有另外一个点：B = [1, 0.25]，我们将它与前面的A相加。

从几何角度来看，这相当于将两个向量的箭头连在一起，得到的位置表示两个向量之和对应的向量（见下图）。

如你所见，将向量B与向量A相加，相当于将A点复制到一个新位置，这个新位置相对于A点初始位置的距离和方向由向量B决定。如果将相同的向量加法应用于平面上的一组点（一个物体），就会在新位置上创建整个物体的副本（见下图）。

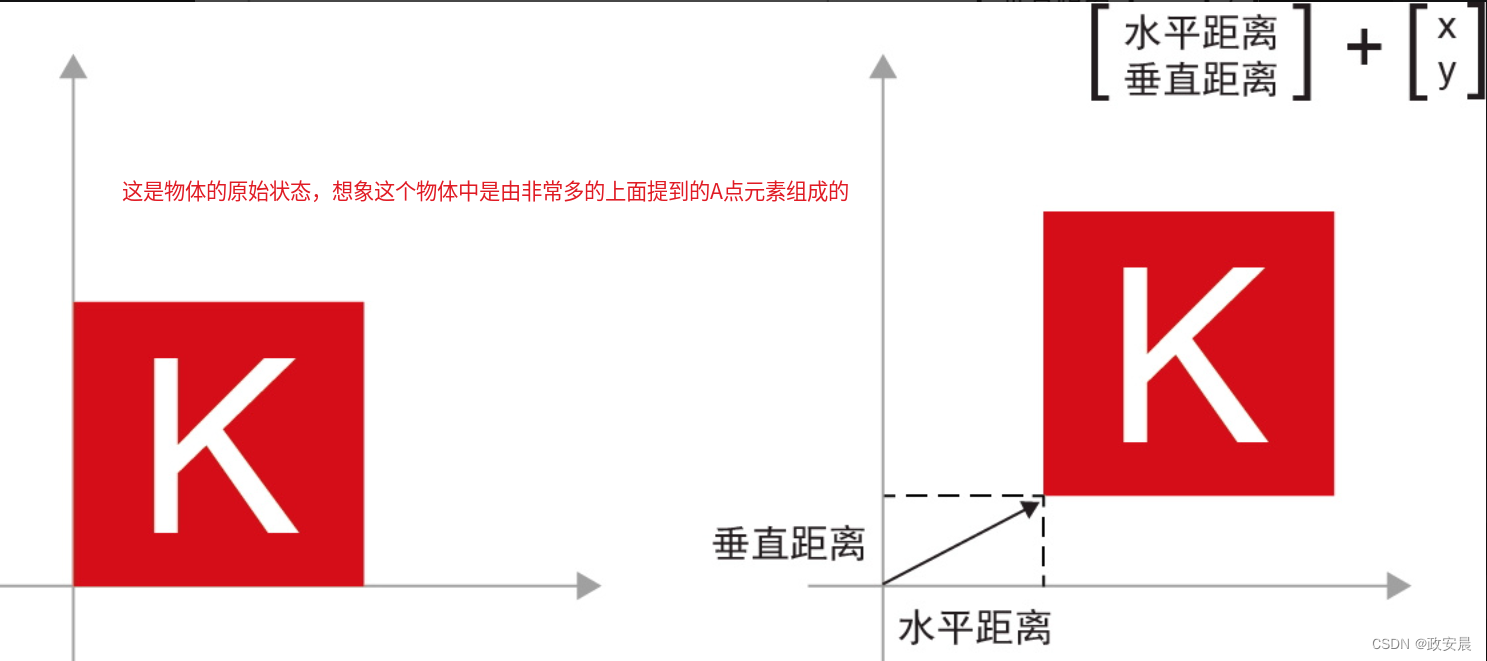
因此，张量加法表示将物体沿着某个方向平移一段距离（移动物体，但不使其变形）。

一般来说，平移、旋转、缩放、倾斜等基本的几何操作都可以表示为张量运算。

机器学习的目的

为高维空间中复杂、高度折叠的数据流形（manifold）找到简洁的表示。

深度学习特别擅长这一点：

它可以将复杂的几何变换逐步分解为一系列基本变换，这与我们展开纸团所采取的策略大致相同。深度神经网络的每一层都通过变换使数据解开一点点，而许多层堆叠在一起，可以实现极其复杂的解开过程。

（更加复杂的知识，咱们将在今后通过实际的示例演绎再为大家讲解。）