引言
在机器学习领域,回归是一种常见的监督学习任务,它主要用于预测数值型目标变量。回归分析能够通过对输入特征与目标变量之间的关系建模,从而对未知数据做出预测。

概念
回归是机器学习中的一种监督学习方法,用于预测数值型目标变量。它通过建立特征与目标变量之间的关系模型,对未知数据做出预测。
举个例子来说明回归的概念:
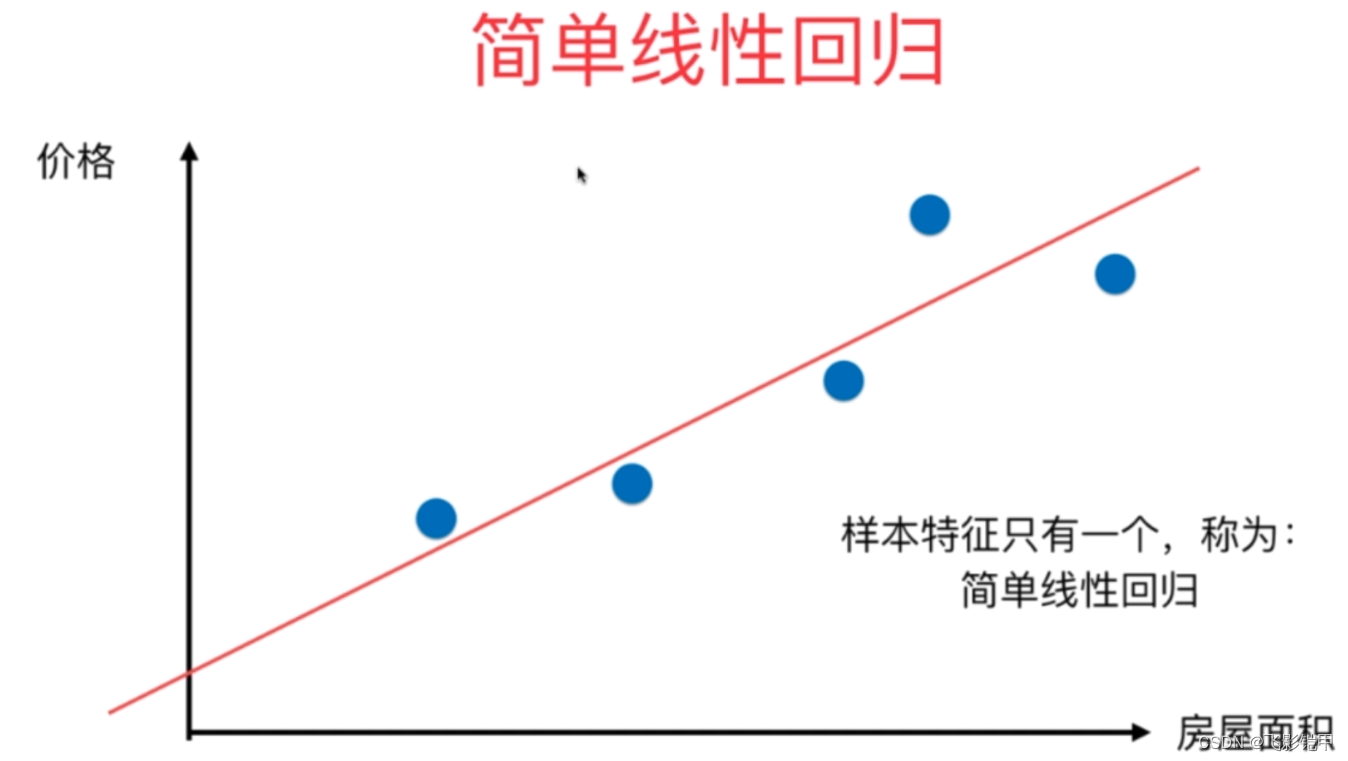
假设我们希望根据房屋的面积来预测其价格。我们可以收集一组包含多个房屋的数据样本,每个样本包含房屋的面积和对应的价格。这些数据样本就构成了我们的训练集。
回归模型的目标是找到一个函数来描述输入特征(房屋的面积)与目标变量(价格)之间的关系。在简单线性回归中,我们假设房屋的价格与面积之间存在着线性关系,即价格可以用面积来预测。我们可以使用最小二乘法来拟合一条直线,使得该直线与所有样本点的误差最小化。
通过得到回归模型,我们可以对未知的房屋面积进行预测。例如,如果有一座新的房屋,我们知道它的面积是100平方米,那么通过回归模型,我们可以预测其价格为150万元。
需要注意的是,回归并不仅限于简单的直线拟合,我们还可以使用多项式回归来描述非线性关系,或者使用其他更复杂的回归算法进行建模。回归模型在许多领域都有广泛的应用,如金融预测、销售预测、医学研究等。它能够帮助我们理解变量之间的关系,并进行准确的数值预测。
常见的回归算法:
-
线性回归(Linear Regression): 线性回归是一种基本且常用的回归算法。它通过拟合一个线性模型来描述特征与目标变量之间的关系。线性回归假设输入特征与目标变量之间存在线性关系,并使用最小二乘法来估计模型参数。线性回归易于实现和解释,但对于非线性关系的数据拟合效果较差。
-
多项式回归(Polynomial Regression): 多项式回归是在线性回归的基础上引入多项式特征的一种扩展形式。通过将特征进行多项式转换,可以更好地拟合复杂的非线性关系。多项式回归能够提高模型的灵活性,但在高维度的情况下容易发生过拟合。
-
岭回归(Ridge Regression): 岭回归是一种正则化线性回归算法,通过加入L2正则化项来缩减模型参数的大小。L2正则化能够有效地减小模型的方差,降低过拟合的风险。岭回归适用于特征之间存在共线性的情况,可以提高模型的泛化能力。
-
Lasso回归(Lasso Regression): Lasso回归是一种使用L1正则化的线性回归算法。与岭回归不同,Lasso回归能够将某些模型参数压缩为零,实现特征选择的效果。L1正则化具有稀疏性,因此Lasso回归常被用于特征选择和模型简化。
-
决策树回归(Decision Tree Regression): 决策树回归是一种非参数化的回归算法,它将输入空间划分为多个区域,并在每个区域内拟合一个局部模型。决策树回归适用于复杂的非线性关系,并且能够处理离散型和连续型特征。然而,决策树容易产生过拟合,因此常常需要剪枝等策略来提高泛化性能。
-
随机森林回归(Random Forest Regression): 随机森林回归是基于决策树的集成学习方法,通过随机选择特征和样本来构建多个决策树。随机森林回归具有较强的鲁棒性和泛化能力,能够应对高维度数据和噪声。此外,它还可以评估特征的重要性,用于特征选择和解释模型。
-
支持向量回归(Support Vector Regression, SVR): 支持向量回归是一种使用支持向量机(SVM)技术进行回归分析的方法。SVR通过将目标变量与一条超平面之间的间隔最大化来拟合模型。SVR适用于非线性关系和高维度数据,并具有较好的泛化性能。然而,SVR对参数的选择敏感,需要进行调优。
总结
本篇博客简单介绍了回归的概念和几种常见的回归算法,包括线性回归、多项式回归、岭回归、Lasso回归、决策树回归、随机森林回归和支持向量回归。每种算法都有其特点和适用范围,可以根据具体问题选择合适的回归算法进行建模和预测。在实际应用中,还可以结合特征工程、模型评估和调参等技巧进一步优化回归模型的性能。





)
)



)








