1. 位图

1.1什么是位图

位图（Bitmap）是一种基于位操作的数据结构，用于表示一组元素的集合信息。它通常是一个仅包含0和1的数组，其中每个元素对应集合中的一个元素。位图中的每个位（或者可以理解为数组的元素）代表一个元素是否存在于集合中。当元素存在时，对应位的值为1；不存在时，对应位的值为0。

位图常用于判断某个元素是否属于某个集合，或者对多个集合做交集、并集或差集等集合运算。它的优点在于速度快，内存空间占用小，能表示大范围的数据。由于它的高效性和节省空间的特性，位图在很多场景中都有广泛的应用。

1.2为什么会有位图

给大家举个例子，假设存在 40 亿个不重复的无符号整数，也就是正数，没排过序，那么给一个无符号的整数，如何判断这个数是否在那 40 亿个数之中呢？

很多人第一想法就是直接遍历这 40 亿个整数，时间复杂度为 O(N)，每次遍历都判断是否等于这个给定的整数就可以了，这个想法对于少量数据是可实行的，但是这里数据有 40 亿个整数，换算成内存就是：40亿 * 4 = 160亿个字节，160亿 * 8 = 1240亿个比特位，1240亿 / 1024 / 1024 / 1024 ≈ 16GB，也就是说通过遍历这 40 亿个整数的话需要使用 16 GB的内存，那么这对于运行内存大的勉强可以实现，对于我们普通的电脑来说，几乎是不可能的。所以通过遍历这 40 亿个整数然后查找的想法是行不通的。

那么又有人会说了，我先将这 40 亿个数字进行排序，然后查找的时候使用二分查找的方式来查询不就可以了吗？我们来看看排序后再而二分查找的时间复杂度为多少：排序的时间复杂度为 O(NlogN)，二分查找的时间复杂度为 O(logN)，总体时间复杂度为 O((N+1)logN)，也就接近于 O(N)，所以这个也是行不通的。

而通过我们的位图实现的话，因为一个数字是否存在只需要使用一个比特位就可以实现，那么这 40 亿个数字总共需要：40亿 / 8 / 1024 / 1024 ≈ 512MB，这样就极大的节省了内存空间。

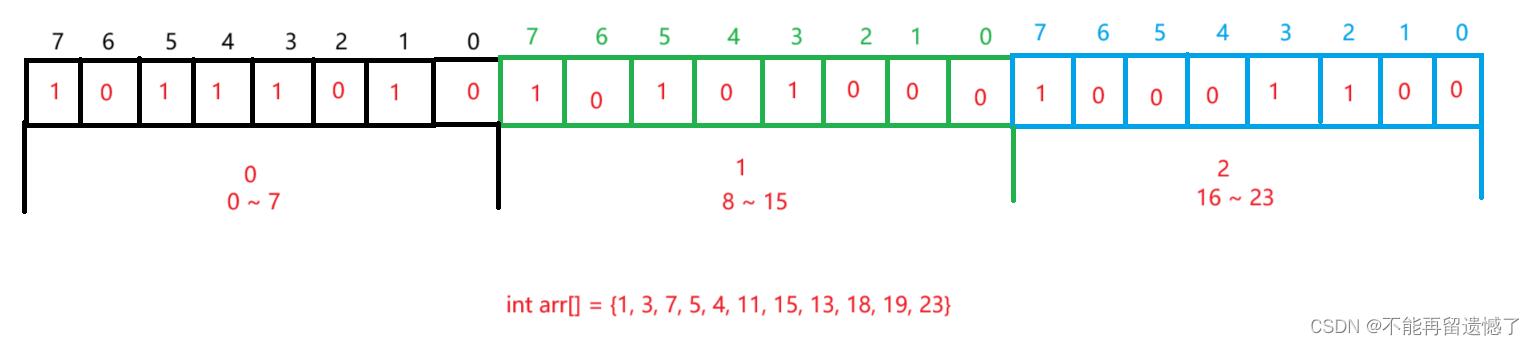
1.3 实现位图

首先我们的位图类中需要存在一个字节数组和计数器用来计算数组中的元素：

public class MyBitSet {private byte[] elem;private int usedSize;public MyBitSet() {//默认给一个字节elem = new byte[1];}public MyBitSet(int n) {//根据给定的整数的最大值来创建数组elem = new byte[n/8 + 1];  //这里只开辟n/8个字节是不够的，需要多一个}
}

然后就是插入操作，我们应该如何标记指定位置为 1 呢？因为一个字节的大小是 8 个比特位，所以数组的下标就可以用 n/8 来表示，这是知道了该元素在数组的哪个下标，再通过 n%8 可以知道该元素在该字节的哪一个比特位。假设我们要存储 13，13 / 8 = 1，那么该元素就存储在数组的 1 下标处，然后将一个字节从右开始的第 13 % 8 = 5 个位置设置为 1，也就是 arr[13/8] |= (1<<(13%8))。

public void set(int val) {//如果给的数字为负数的话，我们这里直接抛出异常//这里也可以不抛出异常，如果我们知道给定的数据中的最小的负数，那么我们可以在插入的时候每个数都加上一个值//使得每个数字都是正数if (val < 0) throw new ArrayIndexOutOfBoundsException();int arrayIndex = val/8;int bitIndex = val%8;elem[arrayIndex] |= (1<<bitIndex);usedSize++;
}

当查看指定数据是否存在的时候，还是通过相同的方法，查看 arr[arrIndex]位置的从右往左的第 bitIndex 上的位置是否为 1：

public boolean get(int val) {if (val < 0) throw new ArrayIndexOutOfBoundsException();int arrayIndex = val/8;int bitIndex = val%8;if ((elem[arrayIndex] & (1<<bitIndex)) != 0) return true;return false;
}

如果我们想要将已经插入的数据删除的话，也是将对应的比特位设置为 0 就可以了：

public void reSet(int val) {if (val < 0) throw new ArrayIndexOutOfBoundsException();int arrayIndex = val/8;int bitIndex = val%8;elem[arrayIndex] &= ~(1<<bitIndex);usedSize--;
}

查看当前位图存在多少数据：

public int getUsedSize() {return this.usedSize;}

上面是我们自己实现的位图，其实 Java 为我们提供了位图 BitSet：

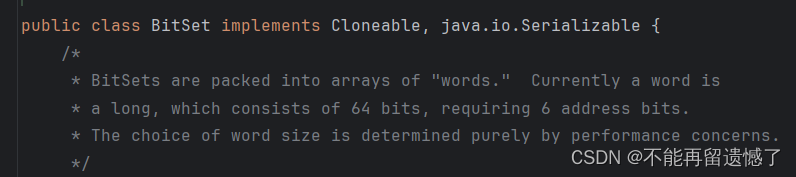
只不过，我们这里数组使用的是 byte，而 BitSet 使用的是 Long：

这里的初始化，数组中元素的个数也是1：

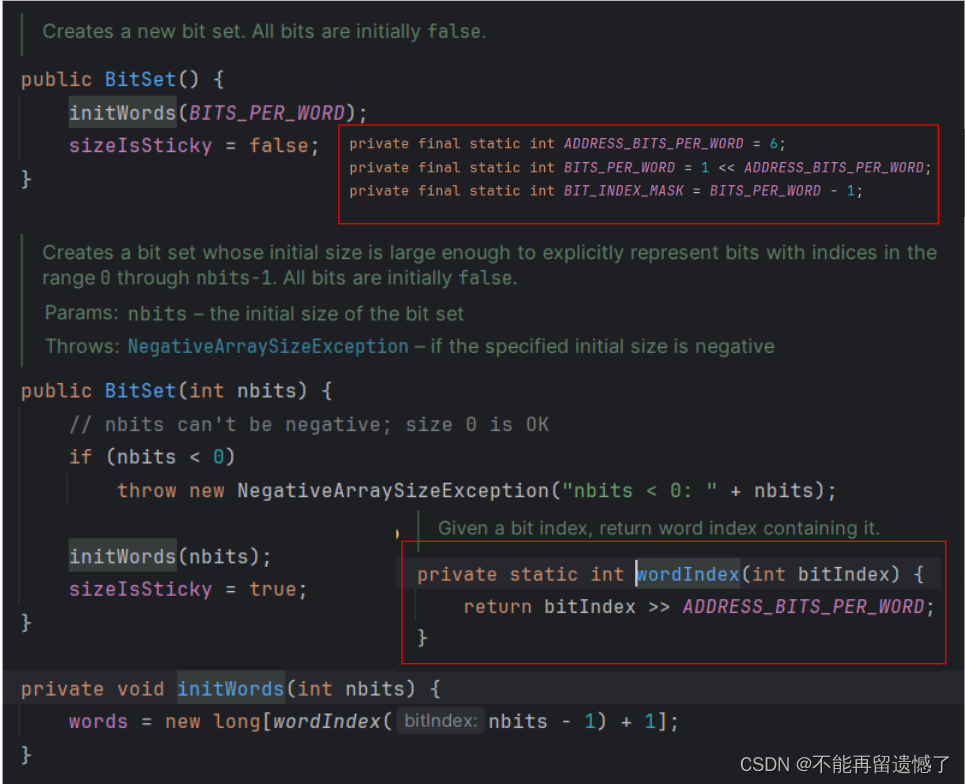
1.4 位图的应用

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

局限性：位图只能操作整数，对于小数的字符串无法处理，所以就出现了布隆过滤器。

2. 布隆过滤器

2.1 什么是布隆过滤器

布隆过滤器（Bloom Filter）是1970年由布隆提出的，它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多，缺点是有一定的误识别率和删除困难。

布隆过滤器的基本原理是将一个元素通过多个哈希函数映射到一个位数组中的多个位置，然后将这些位置置为1。在查询时，检查这些位置是否都是1，如果是，则认为元素可能存在于集合中。需要注意的是，布隆过滤器有可能产生误判（false positive），即认为某个元素存在于集合中，但实际上并不存在；但不会产生误判（false negative），即认为某个元素不存在于集合中，但实际上存在。

布隆过滤器的应用场景包括但不限于防止垃圾邮件、搜索引擎、数据库缓存、数据安全等。例如，在Redis数据库中，可以使用布隆过滤器解决缓存穿透问题，即当查询一个不存在的数据时，直接返回空，而不是再次从数据库中查询。这样可以避免对数据库的过多压力，提高系统的性能和稳定性。

2.2 为什么会有布隆过滤器

对于海量数据的处理，使用普通的方法是无法做到的，虽然位图可以处理大量的数据，但是位图只能处理整数，对于一些字符串，位图是无法处理的，那么有人就会想到使用哈希表来存储，哈希表虽然可以存储多种数据类型的数据，但是存储在哈希表中也需要占用大量的空间。那么如何做到即可以存储整数之外的数据类型，也可以节省空间呢？那就是布隆过滤器，布隆过滤器结合了位图和哈希表，使得布隆过滤器可以应用多种场景。

2.3 布隆过滤器的插入

布隆过滤器的插入其实和位图的插入类似，只不过在布隆过滤器插入之前，会通过多个哈希函数来得到不同的结果，为什么会需要多个哈希函数呢？我们都知道哈希冲突，当我们进行哈希操作的时候，很容易就会发生哈希冲突，通过多个哈希函数计算出来的哈希函数可以大大降低哈希冲突。

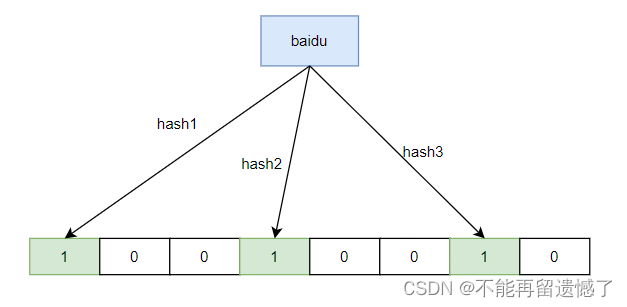
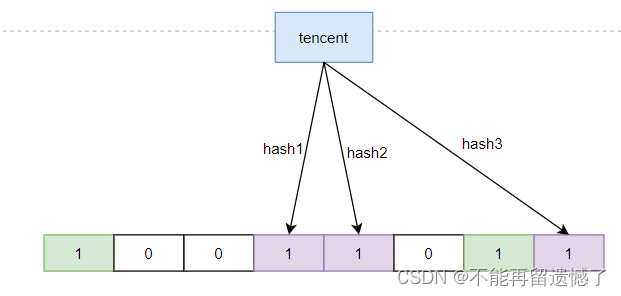
2.4 布隆过滤器的查找

布隆过滤器的查找就是将需要查找的元素，通过多个哈希函数的计算，然后根据计算的值去位图中寻找，如果计算的多个哈希值中某一个位置为 0，那么该元素一定不存在，但是如果所有位置都为 1，也不能一定确定该元素就在布隆过滤器中。假设 baidu 通过哈希函数计算出来的哈希值为1、3、7，tencent 计算出来的哈希值为3、4、8，alibaba 计算出来的哈希值为 2、5、6，而我们要查找的 zijietiaodong 计算出来的哈希值为 1、4、6，那么就不能说 zijietiaodong 一定存在于布隆过滤器中。

2.5 布隆过滤器的模拟实现

首先我们需要构建出几个哈希函数，那么构建多少个哈希函数才合适呢？这里有公式：

• 设bitarray大小为m，样本数量为n，失误率为p
• 使用样本数量n和失误率p可以算出m，公式为：
  
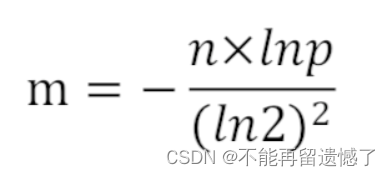
• 所使用哈希函数个数k可以由以下公式求得：
  
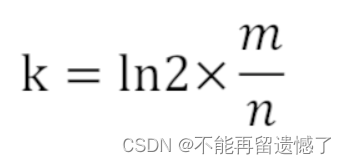
• 通过 bitarray 的大小m和哈希函数的个数可以计算出失误率p：
  

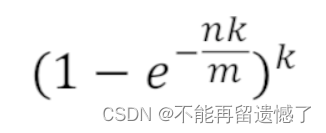
public class SimpleHash {//容量private int cap;//随机种子private int seed;public SimpleHash(int cap, int seed) {this.cap = cap;this.seed = seed;}/*** 将当前的字符串转换为哈希值* @param val* @return*/public int hash(String val) {int result = 0;for (int i = 0; i < val.length(); i++) {result = seed * result + val.charAt(i);}return (cap - 1) & result;}
}

布隆过滤器的初始化：

public class BloomFilter {private static final int DEFAULT_SIZE = 1 << 24;private static final int[] seeds = new int[]{5,7,11,13,31,37,61};private BitSet bitSet;  //位图用来存储元素private SimpleHash[] func;  //存放多个哈希函数private int size;public BloomFilter() {bitSet = new BitSet(DEFAULT_SIZE);func = new SimpleHash[seeds.length];for (int i = 0; i < seeds.length; i++) {func[i] = new SimpleHash(DEFAULT_SIZE,seeds[i]);}}
}

布隆过滤器的插入：

/*** 布隆过滤器的插入* @param val*/
public void set(String val) {if (val == null) return;for (SimpleHash f : func) {bitSet.set(f.hash(val));}size++;
}

布隆过滤器的查找：

/*** 布隆过滤器中查找某个元素是否存在* @param val* @return*/
public boolean contains(String val) {if (val == null) return false;for (SimpleHash f : func) {if (!bitSet.get(f.hash(val))) return false;}return true;  //有误判
}

布隆过滤器不建议进行删除操作，因为在删除一个元素的时候可能会影响其他元素。

2.6 布隆过滤器的优点

1. 增加和查询元素的时间复杂度为：O(K)（K为哈希函数的个数，一般比较小），与数据量大小无关
2. 哈希函数相互之间没有关系，方便硬件进行并行运算
3. 布隆过滤器不需要存储元素本身，在某些对于保密要求比较严格的场合有很大优势
4. 在能够承受一定误判时，布隆过滤器比其他数据结构有很大的空间优势
5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
6. 使用同一组散列函数的布隆过滤器可以进行交、并、差集运算

2.7 布隆过滤器缺陷

1. 误判率：这是布隆过滤器最主要的缺陷。由于哈希函数的随机性和冲突的可能性，即使位数组中的某些位置被置为1，也不一定表示元素一定存在于集合中。因此，布隆过滤器有可能产生误判（false positive），即认为某个元素存在于集合中，但实际上并不存在。
2. 不能删除元素：一旦将元素加入布隆过滤器中，就不能将其删除。这是因为删除操作会破坏位数组中已经记录的信息，导致查询的准确性下降。这也是布隆过滤器的一个主要限制。
3. 不能获取元素本 身
4. 如果采用计数

3. 海量数据面试题

3.1 哈希切割

1. 给定一个超过 100G 大小的log file，log 中存着 IP 地址，设计算法找到出现次数最多的 IP 地址，同样那如果是出现次数 topK 的IP呢？

如果忽略大小的话，我们可以使用 <K,V> 模型来统计每个 IP 出现的次数，但问题就是这里的数据非常多，使用 <K,V> 模型的话，一次性是无法都加载到内存当中的。那么我们将这个大文件分成多个小文件不就可以了？可以是可以，可是如何划分呢？有人会说均分不就可以了？均分可以吗？均分不可以，因为你均分之后，你其中一个文件中的出现次数最多的 IP 地址并不是所有文件中 IP 地址出现次数最多的，那么我们应如何将 IP 地址相同的划分到一个文件呢？

因为 IP 地址本质上也是一个字符串，所以我们可以使用哈希函数先将 IP 地址转换为一个整数，然后将得到的一样的哈希值给放到一个文件中，那么这样相同的 IP 地址最终就会被分到同一个文件中，这种思路叫做 哈希分割

当完成哈希分割之后，我们统计每个文件中 IP 地址出现的次数，最后得到出现次数最多的 IP 地址。

3.2 位图

1. 给定100亿个整数，设计算法找到只出现一次的整数。

这道题目有两种思路：

1. 哈希切割
2. 位图

首先是哈希切割，我们将出现的所有的相同的整数给分割到一个文件中，然后遍历每个文件，统计文件中整数出现的整数的次数，最终得到只出现了一次的整数。

然后第二种思路就是通过位图来解决。但是位图不是只能判断某一个元素是否存在吗？这道题目不是要求出现了一次的整数吗？那么使用位图该如何解决呢？

是的，一个位图只能判断某个元素是否存在，但是两个位图就可以判断某个元素出现的次数了，两个位图的相同位置可能的结果是 00、01、10和11，我们使用 00 表示该元素未出现，01 表示该元素出现了一次，10 表示出现了两次，11表示出现的次数超过 2 次。

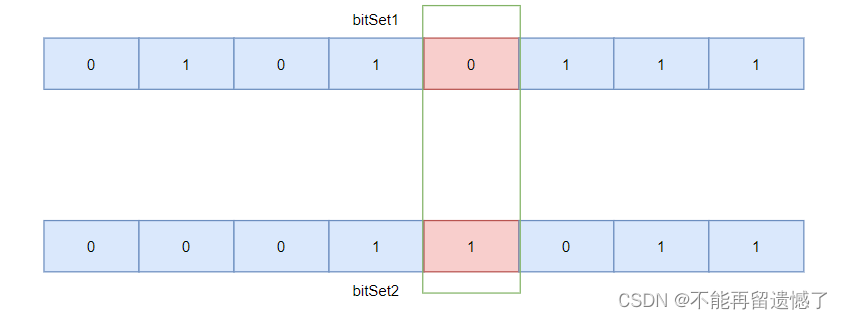
这是使用了两位位图的情况，如果我就想只用一个位图解决可以吗？可以的，之前位图一个比特位表示一个元素，这里我们可以使用两个比特位来表示一个元素。一个字节之前可以表示 8 个元素，现在我只表示 4 个元素，那么 arrIndex 就为 n / 4，bitIndex 就为 2*(n % 4)，这样每两个比特位可以表示的结果就有 00、01、10、11，这样就可以判断出只出现了一次的整数了。

2. 给定两个文件，分别有 100亿 个整数，我们只有一个 G 的内存，如何找到两个文件的交集？

同样是两种思路：

1. 哈希切割
2. 位图

我们两个文件都使用相同的哈希函数对文件中的数据进行切割，切割完成之后，分别遍历两个相同下标的文件，看这两个文件中是否有相同的元素。

第二种思路，使用位图，分别使用一个位图，只用 0 和 1 标识某个元素是否存在，都存入位图之后，再分别遍历这两个位图，如果相同位置上的数据都为 1 的话，该位置表示的整数就是两个文件中的交集。

3.3 布隆过滤器

给两个文件，分别有 100亿 个query，我们只有 1G 内存，如何找到两个文件的交集？分别给出精确算法近似算法。

既然提到精确算法和近似算法，那么这个问题就有两种思路可以解决：

1. 哈希切割（精确算法）
2. 布隆过滤器（近似算法）

这个做法和上面类似，分别遍历两个文件，将文件分割成 n 个大小的文件，然后再分别遍历对应的文件，找两个文件中存在的 query。

第二种思路是布隆过滤器，先遍历一个文件，将该文件中的 query 通过哈希函数映射到布隆过滤器中，然后再遍历第二个文件，遍历的同时，在布隆过滤器中看该元素是否存在，存在则为交集。