向量搜索查询faiss、annoy

首先介绍annoy :
转发空间：https://download.csdn.net/blog/column/10872374/114665212

Annoy是高维空间求近似最近邻的一个开源库。

Annoy构建一棵二叉树，查询时间为O(logn)。

Annoy通过随机挑选两个点，并使用垂直于这个点的等距离超平面将集合划分为两部分。

如图所示，图中灰色线是连接两个点，超平面是加粗的黑线。按照这个方法在每个子集上迭代进行划分。
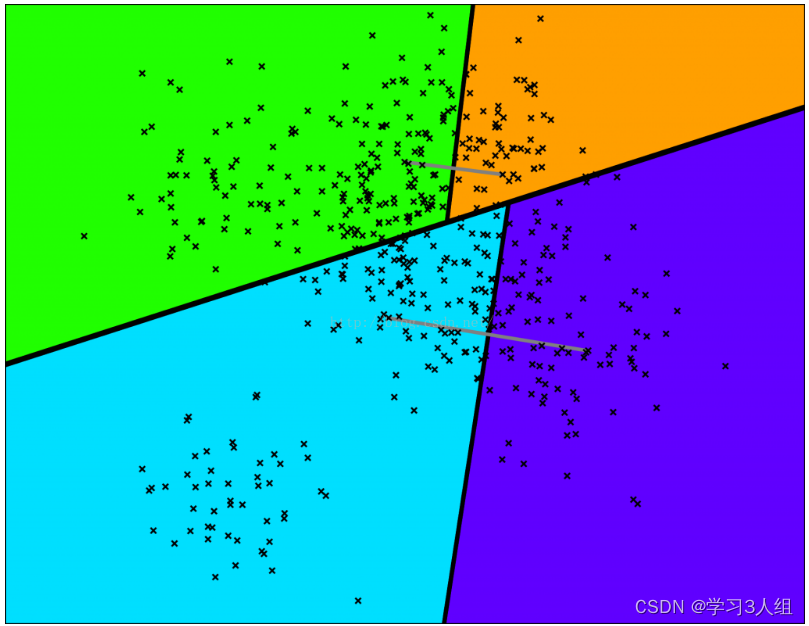
在这里插入图片描述

依此类推，直到每个集合最多剩余k个点，下图是一个k = 10 的情况。

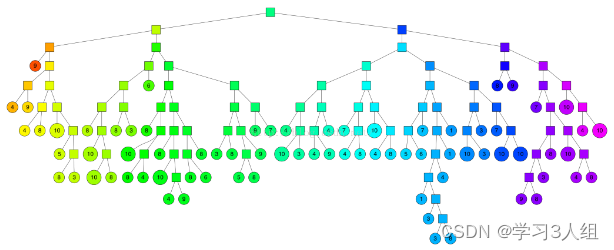
在这里插入图片描述

n_trees在构建时提供，并影响构建时间和索引大小。较大的值将给出更准确的结果，但更大的索引。

search_k在运行时提供，并影响搜索性能。较大的值将给出更准确的结果，但将需要更长的时间返回。

代码实现：

pip install annoy == 1.17.0 -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn

from tqdm import tqdm
import pandas as pd
import time
import numpy as np
from annoy import AnnoyIndex
from sentence_transformers import SentenceTransformer, InputExample
from sentence_transformers import models, losses
from torch.utils.data import DataLoader
from sentence_transformers import SentenceTransformer, util
from sentence_transformers import SentenceTransformer, SentencesDataset, InputExample, evaluation, losses, models
from torch.utils.data import DataLoader
model = SentenceTransformer(r'327_6epoch_64batchdjwSaveModel/djwSaveModel')
emb1 = model.encode("美赞臣安婴儿A+亲舒婴儿奶粉1段850克0-12个月宝宝")
print(emb1.shape)
emb2 = model.encode("美赞臣亲舒一段领券满减")
emb3 = model.encode("真手表打火机带手电筒真车钥匙电子手表打火机充电防风送男友潮")
cos_sim = util.pytorch_cos_sim(emb1, emb2)
cos_sim1 = util.pytorch_cos_sim(emb3, emb2)
print("Cosine-Similarity:", cos_sim,cos_sim1)
corpus_data = pd.read_csv("corpus.tsv",sep="\t",header=None,names=['doc_id','title'])#读取csv文件
corpus_title_data=corpus_data['title'].values
qrels_train_data = pd.read_csv("qrels.train.tsv",sep="\t",header=None,names=['query_id','doc_id'])#读取csv文件
dev_id_query_data =[]
dev_querytxt_data=[]
with open("dev.query.txt","r",encoding='utf-8') as f:lines=f.readlines()for line in lines:dev_id_query_data.append(line.split("\n")[0].split("\t"))dev_querytxt_data.append(line.split("\n")[0].split("\t")[1])
print(len(dev_querytxt_data))
print(dev_querytxt_data[0:10])
f=128
t = AnnoyIndex(f, 'angular')  # Length of item vector that will be indexed
for index_i, i in tqdm(enumerate(dev_querytxt_data)):  # len 是1000embi = model.encode(i)t.add_item(index_i, embi)# if index_i==100:break
for index_j, j in tqdm(enumerate(corpus_title_data)):  # 1001500embj = model.encode(j)t.add_item(index_j + 1000, embj)# if index_j == 100: break
t.build(500)
t.save('327_6epoch_64batchdjwSaveModel_embeedding.ann')

两个超参数需要考虑：树的数量n_trees和搜索过程中检查的节点数量search_k

基本上，建议在可用负载量的情况下尽可能大地设置n_trees，并且考虑到查询的时间限制，建议将search_k设置为尽可能大。

n_trees: 在构建期间提供，影响构建时间和索引大小。值越大，结果越准确，但索引越大。

search_k: 在运行时提供，并影响搜索性能。值越大，结果越准确，但返回的时间越长。如果不提供，就是n_trees * n， n是最近邻的个数

u = AnnoyIndex(f, 'angular')
u.load('ceshi_embeedding.ann')
for i in range(100):temp=u.get_nns_by_item(i,4)print(dev_querytxt_data[i])for idx in temp[1:]:print(corpus_title_data[idx-1000])print("------------------------------------------------------------")Facebook: 亿级向量相似度检索库Faiss原理
Faiss的核心原理其实就两个部分：
Product Quantizer, 简称PQ.
Inverted File System, 简称IVF.

2 Product Quantizer

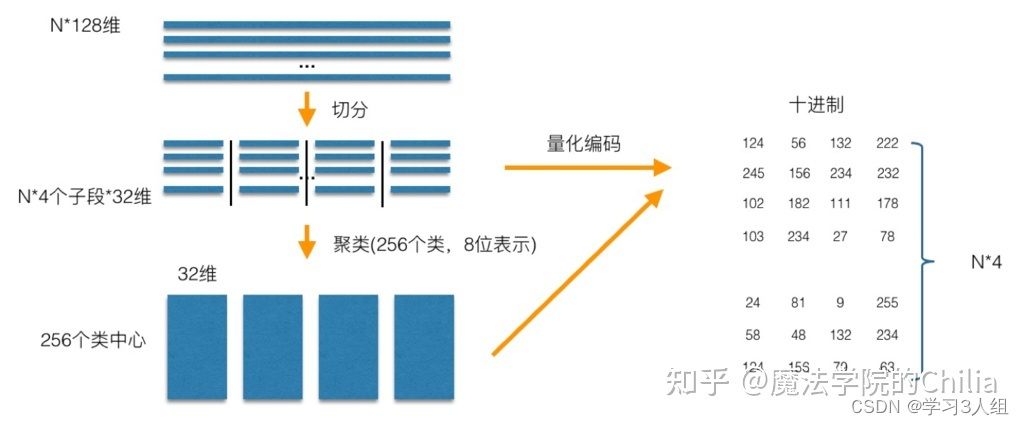
在这里插入图片描述

在做PQ之前，首先需要指定一个参数M，这个M就是指定向量要被切分成多少段，在上图中M=4，所以向量库的每一个向量就被切分成了4段，然后把所有向量的第一段取出来做Clustering得到256个簇心（256是一个作者拍的经验值）；再把所有向量的第二段取出来做Clustering得到256个簇心，直至对所有向量的第N段做完Clustering，从而最终得到了256*M个簇心。

做完Cluster，就开始对所有向量做Assign操作。这里的Assign就是把原来的N维的向量映射到M个数字，以N=128，M=4为例，首先把向量切成四段，然后对于每一段向量，都可以找到对应的最近的簇心 ID，4段向量就对应了4个簇心 ID，一个128维的向量就变成了一个由4个ID组成的向量，这样就可以完成了Assign操作的过程 – 现在，128维向量变成了4维，每个位置都只能取0~127，这就完成了向量的压缩。

完成了PQ的Pre-train，就可以看看如何基于PQ做向量检索了
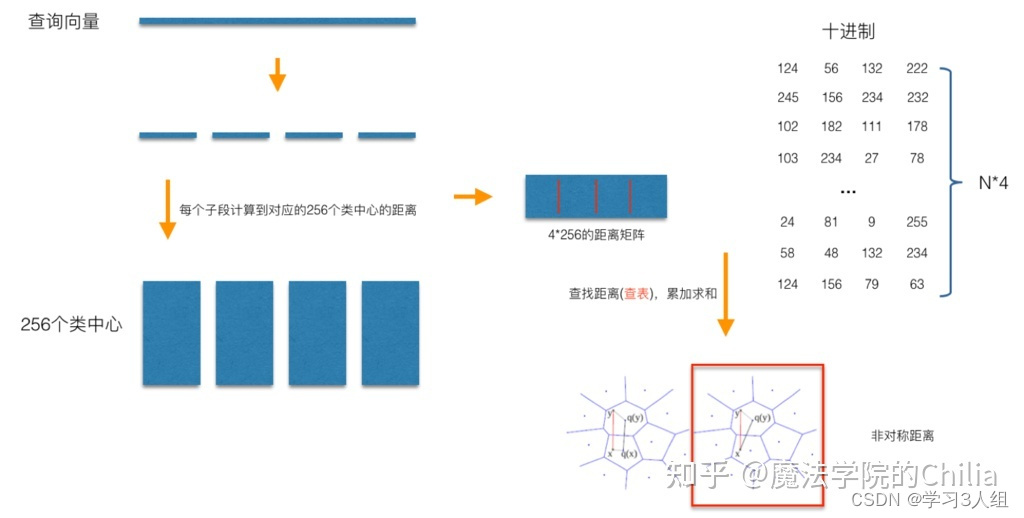
在这里插入图片描述

同样是以N=128，M=4为例，对于每一个查询向量，以相同的方法把128维分成4段32维向量，然后计算每一段向量与之前预训练好的簇心的距离，得到一个4*256的表。然后就可以开始计算查询向量与库里面的向量的距离。此时，库的向量已经被量化成M个簇心 ID，而查询向量的M段子向量与各自的256个簇心距离已经预计算好了，所以在计算两个向量的时候只用查M次表，比如的库里的某个向量被量化成了[124, 56, 132, 222], 那么首先查表得到查询向量第一段子向量与其ID为124的簇心的距离，然后再查表得到查询向量第二段子向量与其ID为56的簇心的距离…最后就可以得到四个距离d1、d2、d3、d4，查询向量跟库里向量的距离d = d1+d2+d3+d4。所以在提出的例子里面，使用PQ只用4×256次128/4维向量距离计算加上4xN次查表，而最原始的暴力计算则有N次128维向量距离计算，很显然随着向量个数N的增加，后者相较于前者会越来越耗时。

2 Inverted File System
要想减少需要计算的目标向量的个数，做法就是直接对库里所有向量做KMeans Clustering，假设簇心个数为1024。那么每来一个query向量，首先计算其与1024个粗聚类簇心的距离，然后选择距离最近的top N个簇，只计算查询向量与这几个簇底下的向量的距离，计算距离的方法就是前面说的PQ。Faiss具体实现有一个小细节，就是在计算查询向量和一个簇底下的向量的距离的时候，所有向量都会被转化成与簇心的残差，这应该就是类似于归一化的操作，使得后面用PQ计算距离更准确一点。使用了IVF过后，需要计算距离的向量个数就少了几个数量级，最终向量检索就变成一个很快的操作。

import faissnlist = 100
m = 8 ##每个向量分8段
k = 4 ##求4-近邻
quantizer = faiss.IndexFlatL2(d)    # 内部的索引方式依然不变
index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8) # 每个向量都被编码为8个字节大小
index.train(xb)
index.add(xb)
index.nprobe = 10                
D, I = index.search(xq, k)          # 检索
print(I[-5:])