代码随想录Day43 | 1049. 最后一块石头的重量 II 494. 目标和
- 1049.最后一块石头的重量II
- 494.目标和
- 474.一和零
- 01背包
- 01背包应用问题
1049.最后一块石头的重量II
文档讲解:代码随想录
视频讲解: 这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II
状态
主要目的就是将石头分成重量和相近的两堆,然后最后两堆相减重量和最小。所以还是先求得sum/2,然后以0~sum/2为背包容量,来统计当前dp[j]的j容量下,从stones中选取任意数量的石头,使得和为不大于j的最大值。
- dp数组
dp[j]表示在容量j下,选取任意数量的石头,不大于j的最大和 - 递推公式
dp[j] = max(dp[j],dp[j-stones[i])+stones[i]) - 初始化
全是正数结果,所以可以初始化为0
dp[0] = 0 - 遍历顺序
先石头再背包,背包倒序 - 打印dp数组
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int i = 0;i<stones.size();i++){sum+=stones[i];}int target = sum/2;//dp 当前不大于j的最大和vector<int> dp(target+1,0);for(int i = 0;i<stones.size();i++){for(int j = target;j>=stones[i];j--){dp[j] = max(dp[j],dp[j-stones[i]]+stones[i]);}}return sum-2*dp[target];}
};
494.目标和
文档讲解:代码随想录
视频讲解: 装满背包有多少种方法?| LeetCode:494.目标和
状态
一道组合问题,可以按照回溯方法求解,但复杂度过高。
使用动态规划的方法来解决组合问题
同样和为sum,所有正数和设为x,那么所有负数的和绝对值就是sum-x。那么我们要求的正数加负数的结果就是2x-sum。所以对于target我们的x可以表示为x = (target+sum)/2;
那么就是容量为0~x的背包,从数组中任意选取数字,使得其和相加为x。
- dp数组
dp[j]表示当前容量为j,dp[j]就是能够选取使得和为j的方法数 - 递推公式
dp[j]中j = j-nums[i] + nums[i],也即是说对于数组中每一个数nums[i]都有可能存在一个数,两个数相加为j,那么dp[j]的总次数就是每个nums[i]存在对应的对值的个数之和。
dp[j] += dp[j-nums[i]] - 初始化
dp[0] = 1;
相当于是和为0默认开始为1,但如果后续的和目标为0,那么值会继续增加 - 遍历顺序
先数字,再背包 - 打印dp数组
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for(int i=0;i<nums.size();i++){sum+=nums[i];}if(abs(target) > sum) return 0;//如果sum+target没有办法被2整除 也不存在//x = (sum+target)/2if((sum+target)%2 == 1) return 0;int x = (sum+target)/2;//dp数组vector<int> dp(x+1,0);dp[0] = 1;for(int i = 0;i<nums.size();i++){for(int j = x;j>=nums[i];j--){dp[j] += dp[j-nums[i]];}}return dp[x];}
};
474.一和零
文档讲解:代码随想录
视频讲解: 装满这个背包最多用多少个物品?| LeetCode:474.一和零
状态
m个0 和 n个1 是两个背包
- dp数组
dp[i][j]表示集合中有i个0,j个1的最长集合长度。 - 递推公式
假设要增加的字符串中拥有x个0,y个1那么dp[i][j] = dp[i-x][j-y]+1;
dp[i][j] = max(dp[i][j],dp[i-x][j-y]+1); - 初始化
全部初始化为0。 - 遍历顺序
先物品(字符串)再背包(0和1的个数限制)背包倒序 - 打印dp
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {//实际上是1维dp只不过是两个背包所以使用二维数组统计vector<vector<int>> dp(m+1,vector<int>(n+1,0));//遍历每个字符串统计0和1的个数for(string str : strs){int x = 0;int y = 0;for(char c : str){if(c == '0') x++;if(c == '1') y++;}//遍历背包for(int i = m;i>=x;i--){for(int j = n;j>=y;j--){dp[i][j] = max(dp[i][j],dp[i-x][j-y]+1);}}}return dp[m][n];}
};
01背包
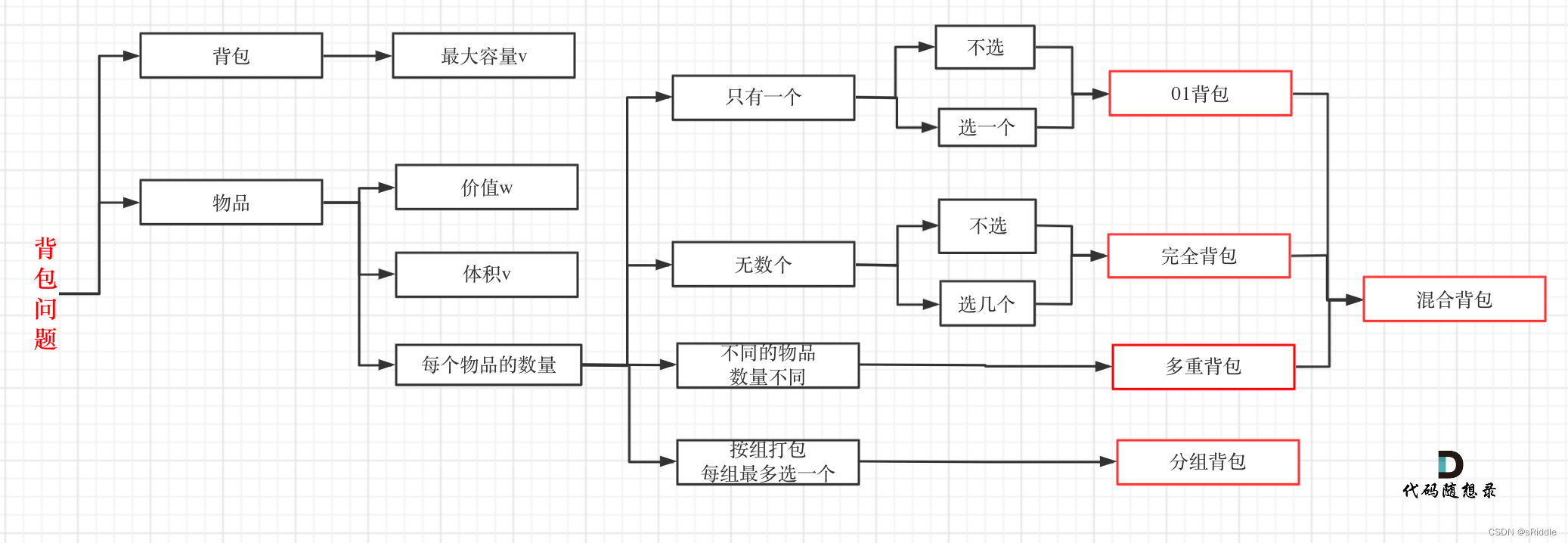
可以看到对于物品数量只有一个的问题一般都是使用01背包解决。这就提示我们需要注意分辨题目中哪个是背包哪个是物品。
01背包的初始化一般都初始化为0。
01背包应用问题
- 给定背包容量,求能够装满背包的最大价值
- 给定背包容量,求能否刚好装满背包
- 给定背包容量,从物品中选择最多能装多少
- 给定背包容量,有多少种方法能够装满
- 给定背包容量,装满背包最多有多少物品


)
![[项目管理] 如何使用git客户端管理gitee的私有仓库](http://pic.xiahunao.cn/[项目管理] 如何使用git客户端管理gitee的私有仓库)

)


真题解析#中国电子学会#全国青少年软件编程等级考试)




)

)


)
)