题目

题目链接
给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

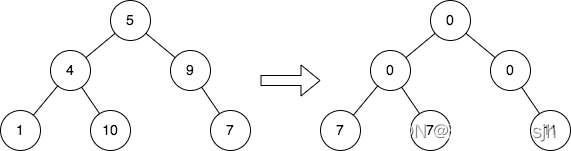
输入：root = [5,4,9,1,10,null,7]
输出：[0,0,0,7,7,null,11]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。

• 值为 5 的节点没有堂兄弟，所以值修改为 0 。
• 值为 4 的节点没有堂兄弟，所以值修改为 0 。
• 值为 9 的节点没有堂兄弟，所以值修改为 0 。
• 值为 1 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
• 值为 10 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
• 值为 7 的节点有两个堂兄弟，值分别为 1 和 10 ，所以值修改为 11 。

示例 2：

输入：root = [3,1,2]
输出：[0,0,0]
解释：上图展示了初始的二叉树和修改每个节点的值之后的二叉树。

• 值为 3 的节点没有堂兄弟，所以值修改为 0 。
• 值为 1 的节点没有堂兄弟，所以值修改为 0 。
• 值为 2 的节点没有堂兄弟，所以值修改为 0 。

提示：
树中节点数目的范围是 [1, 10⁵] 。
1 <= Node.val <= 10⁴

思路

使用层序遍历法模拟即可 ，使用队列来进行节点存储

代码

class Solution {
public:TreeNode* replaceValueInTree(TreeNode* root) {if (!root) return nullptr;  root->val = 0;  queue<TreeNode*> q;  q.push(root);  int pre = 0;  while (!q.empty()) {  int size = q.size();  int sum = 0;  for (int i = 0; i < size; i++) {  TreeNode* cur = q.front();  q.pop();  cur->val = pre - cur->val;  TreeNode* left = cur->left;  TreeNode* right = cur->right;  int val = (left ? left->val : 0) + (right ? right->val : 0);  if (left) {  q.push(left);  left->val = val;  }  if (right) {  q.push(right);  right->val = val;  }  sum += val;  }  pre = sum;  }  return root;  }
};

结果