这是树的第10篇算法，力扣链接。
给定两个整数数组
inorder和postorder，其中inorder是二叉树的中序遍历，postorder是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。示例 1:
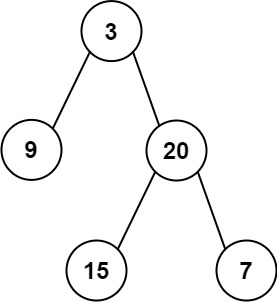
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出：[3,9,20,null,null,15,7]
回忆一下中序遍历和后序遍历。
中序遍历 (Inorder Traversal)
在中序遍历中，我们按照以下顺序遍历树中的节点：
- 遍历左子树
- 访问根节点
- 遍历右子树
对于二叉搜索树（BST），中序遍历会按照升序访问所有节点，因为二叉搜索树的特点是左子节点的值小于根节点的值，根节点的值小于右子节点的值。
后序遍历 (Postorder Traversal)
后序遍历的顺序是：
- 遍历左子树
- 遍历右子树
- 访问根节点
后序遍历常用于删除或释放树中的节点。因为你在删除节点之前先访问其子节点，这样可以安全地删除每个节点。
假设有一棵二叉树如下：
A/ \B C/ \ \ D E F对这棵树进行不同的遍历会得到以下结果：
- 中序遍历：
D, B, E, A, C, F。首先遍历左子树（D, B, E），然后是根节点（A），最后是右子树（C, F）。- 后序遍历：
D, E, B, F, C, A。首先是左子树（D, E, B），然后是右子树（F, C），最后是根节点（A）。
这道题和上一篇算法的前序遍历类似，这不过这里的后序遍历涉及到一定的逆逻辑，例如根节点是最后一个节点，右子树的范围到 len(postorder)-1-len(inorder[index+1:])
func buildTree(inorder []int, postorder []int) *TreeNode {if len(postorder) == 0 {return nil}index := 0for ; index < len(inorder); index++ {if inorder[index] == postorder[len(postorder)-1] {break}}result := &TreeNode{Val: postorder[len(postorder)-1]}result.Right = buildTree(inorder[index+1:], postorder[len(postorder)-1-len(inorder[index+1:]):len(postorder)-1])result.Left = buildTree(inorder[:index], postorder[:len(postorder)-1-len(inorder[index+1:])])return result
}
当然，也可以试试迭代的方法。
func buildTree(inorder []int, postorder []int) *TreeNode {if len(postorder) == 0 {return nil}result := &TreeNode{Val: postorder[len(postorder)-1]}stack := []*TreeNode{result}inorderIndex := len(inorder) - 1for i := len(postorder) - 2; i >= 0; i-- {node := stack[len(stack)-1]if node.Val != inorder[inorderIndex] {node.Right = &TreeNode{Val: postorder[i]}stack = append(stack, node.Right)} else {for len(stack) > 0 && stack[len(stack)-1].Val == inorder[inorderIndex] {node = stack[len(stack)-1]stack = stack[:len(stack)-1]inorderIndex--}node.Left = &TreeNode{Val: postorder[i]}stack = append(stack, node.Left)}}return result
}
