难度参考

        难度：中等

        分类：二叉树

        难度与分类由我所参与的培训课程提供，但需要注意的是，难度与分类仅供参考。且所在课程未提供测试平台，故实现代码主要为自行测试的那种，以下内容均为个人笔记，旨在督促自己认真学习。

题目

        给出一棵完全二叉树，求出该树的节点个数！

        输入：root=[1,2,3,4,5,6]
        输出：6
        示例2:
        输入：root=[]
        输出：0
        示例3:
        输入：root=[1]
        输出：1
        提示：
        树中节点的数目范围是[0,5*10^4]
        0<=Node.val<=5*10^4
        题目数据保证输入的树是完全二叉树

思路

        对于这道题目要求计算一个完全二叉树的节点个数，可以利用完全二叉树的性质来解决，而不需要对整个树进行遍历。

        完全二叉树是指除了最后一层外，每一层的节点都被填满，并且最后一层的节点靠左排列的二叉树。简单来说，完全二叉树是一种具有最优结构的二叉树。

        下面是一个完全二叉树的示例：

      A/   \B     C/ \   /D   E F

        在这个示例中，树的每一层都被节点填满，最后一层的节点靠左排列。

        需要注意的是，对于完全二叉树，叶节点只会出现在最后两层，并且最后一层的叶节点都靠左排列。

        完全二叉树的性质包括：

1. 对于树的任意节点，如果它的深度（从根节点到达该节点的路径的长度）为 d，则以该节点为根的子树一定是一个高度为 h-d+1 的满二叉树。

   • 这是因为完全二叉树的定义要求除了最后一层外，其他层都是满的，而最后一层的节点从左到右连续排列。

2. 一棵高度为 h 的满二叉树，其节点个数为 2^h-1。

        完全二叉树与满二叉树有一定的关系，但并不是完全一样的概念。

        满二叉树是一种特殊的二叉树，它的每一层都被节点填满，所有的叶节点都在同一层上。换句话说，满二叉树的节点数达到了最大值。满二叉树的层数是固定的。

        而完全二叉树是除了最后一层外，每一层的节点都被填满，并且最后一层的节点靠左排列。完全二叉树的节点数可以少于满二叉树，最后一层不一定是满的。

        所以可以说，满二叉树是完全二叉树的一种特殊情况，但完全二叉树不一定是满二叉树。完全二叉树的层数可以少于满二叉树的层数，节点数也可以少于满二叉树的节点数。

        下面是一个满二叉树的示例：

      A/   \B     C/ \   / \D   E F   G

        基于上述性质，我们可以采用以下步骤来计算完全二叉树的节点个数：

1. 首先，计算树的左子树和右子树的深度 leftDepth 和 rightDepth。

2. 如果 leftDepth 等于 rightDepth，则说明左子树是一个满二叉树，且其节点个数可以通过公式 2^leftDepth-1 计算得到。

   • 在这种情况下，我们只需要递归计算右子树的节点个数，然后加上左子树的节点个数和根节点，即可得到完整的节点个数。

3. 如果 leftDepth 不等于 rightDepth，则说明右子树是一个满二叉树，且其节点个数可以通过公式 2^rightDepth-1 计算得到。

   • 在这种情况下，我们只需要递归计算左子树的节点个数，然后加上右子树的节点个数和根节点，即可得到完整的节点个数。

        通过实现上述步骤，我们可以快速地计算出完全二叉树的节点个数。

示例

        假设我们有以下二叉树：

     1/   \2     3/ \   /
4   5 6

        首先，根节点存在，我们开始计算左子树的高度。从根节点1开始，我们通过左子节点2，再通过左子节点4，没有更多的左子节点，此时左子树的高度为3。

        接下来，我们计算右子树的高度。从根节点1开始，我们通过右子节点3，再通过左子节点6，没有更多的右子节点，此时右子树的高度为2。

        由于左子树的高度(3)不等于右子树的高度(2)，所以我们知道右子树是完全二叉树。现在，我们递归地计算右子树的节点个数。右子树只有一个节点6，所以它的节点个数为1。

        由于左子树的高度(3)大于右子树的高度(2)，所以我们知道左子树不是完全二叉树。我们需要递归地计算左子树的节点个数。左子树有两个子节点4和5，因此左子树的节点个数为2。

        最后，我们将左子树的节点个数(2)、右子树的节点个数(1)和根节点(1)相加，得到整个二叉树的节点个数为6。

梳理

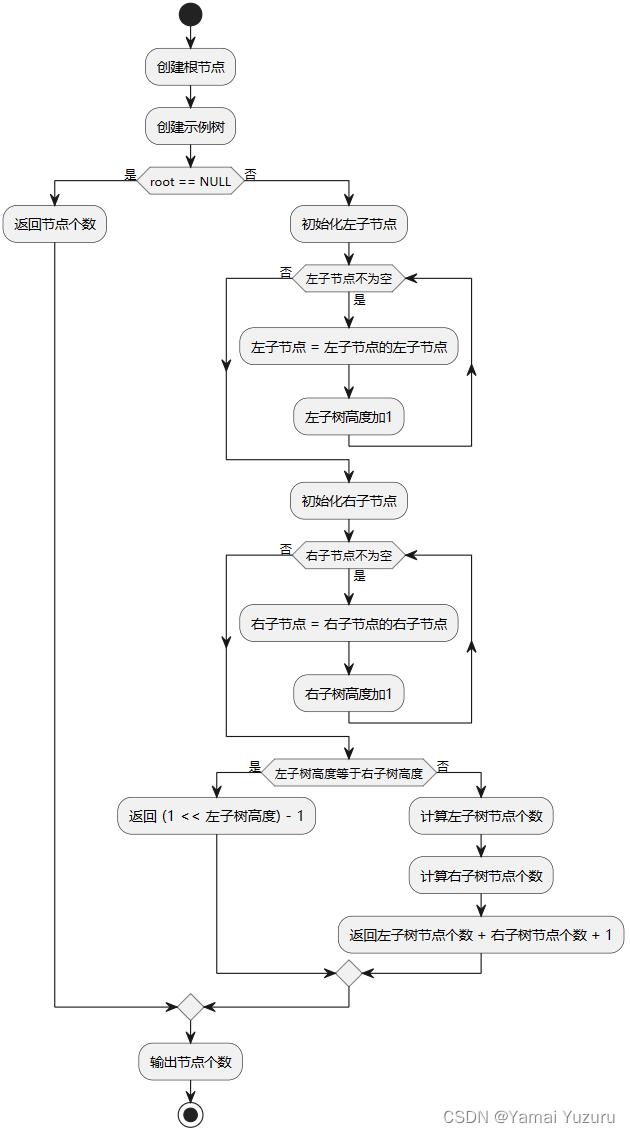
        我们通过判断左子树的高度和右子树的高度来确定给定二叉树是否是完全二叉树。

        判断一个二叉树是否是完全二叉树的方法如下：

1. 首先，我们计算左子树和右子树的高度，使用两个循环分别计算它们的高度。
2. 如果左子树的高度等于右子树的高度，说明左子树是一个满二叉树（即每个节点都有两个子节点），而右子树可能是一个完全二叉树。在完全二叉树中，所有的节点都尽量靠左排列，且最后一层节点从左到右依次填充。因此，在满二叉树的情况下，我们可以使用一个简单的公式计算出左子树的节点个数：(1 << leftHeight) - 1。其中，<< 是位移运算符，表示将1左移leftHeight位，即乘以2的leftHeight次方，然后减去1。
3. 如果左子树的高度不等于右子树的高度，说明左子树不是一个满二叉树，而右子树可能是一个完全二叉树。在这种情况下，我们递归地计算左子树和右子树的节点个数，并将结果相加再加上根节点的1。

        通过这种判断逻辑，我们可以正确地计算给定二叉树的节点个数。

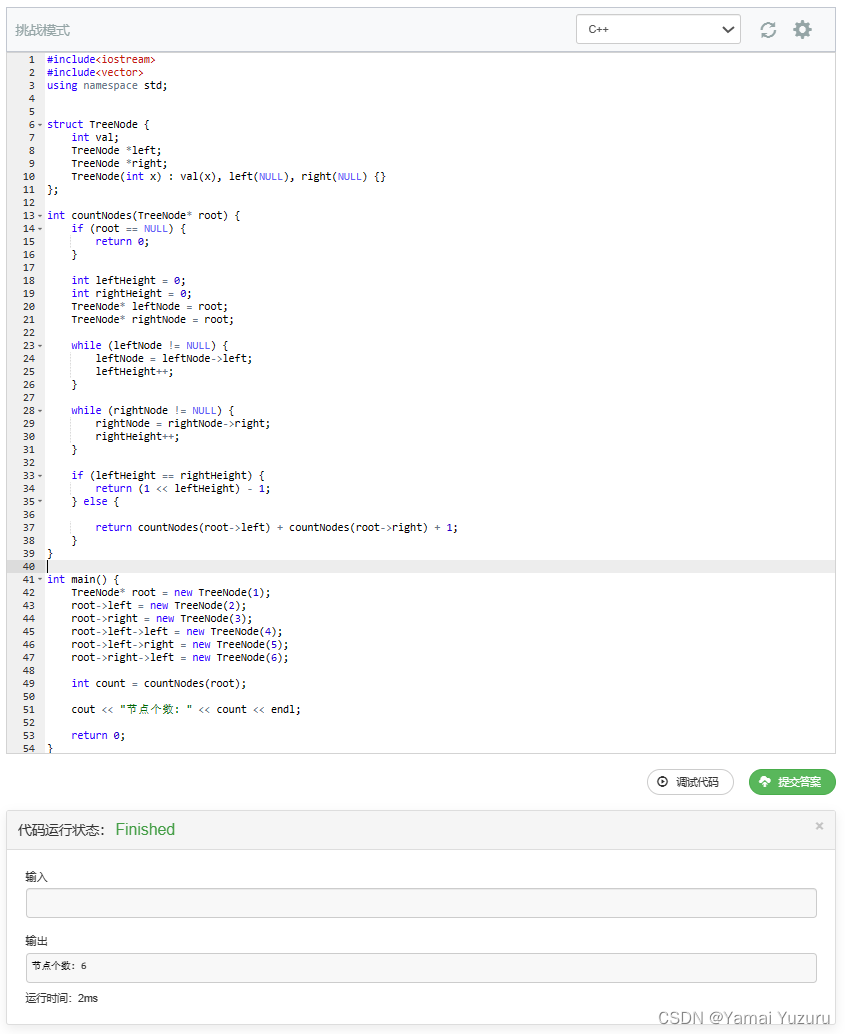
代码

#include<iostream>
#include<vector>
using namespace std;// 二叉树的节点定义
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};// 计算完全二叉树的节点个数
int countNodes(TreeNode* root) {if (root == NULL) {return 0;}int leftHeight = 0;int rightHeight = 0;TreeNode* leftNode = root;TreeNode* rightNode = root;// 计算左子树的高度while (leftNode != NULL) {leftNode = leftNode->left;leftHeight++;}// 计算右子树的高度while (rightNode != NULL) {rightNode = rightNode->right;rightHeight++;}// 如果左子树的高度等于右子树的高度，则说明左子树是完全二叉树if (leftHeight == rightHeight) {// 计算左子树的节点个数：2^leftHeight-1，加上根节点1，即为总节点个数return (1 << leftHeight) - 1;} else {// 如果左子树的高度不等于右子树的高度，则说明右子树是完全二叉树// 计算右子树的节点个数：2^rightHeight-1，加上根节点1，即为总节点个数return countNodes(root->left) + countNodes(root->right) + 1;}
}int main() {// 构建示例树 [1,2,3,4,5,6]TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);root->right->left = new TreeNode(6);// 计算节点个数int count = countNodes(root);// 输出结果cout << "节点个数: " << count << endl;return 0;
}

进阶

        如果是一棵普通二叉树？

思路

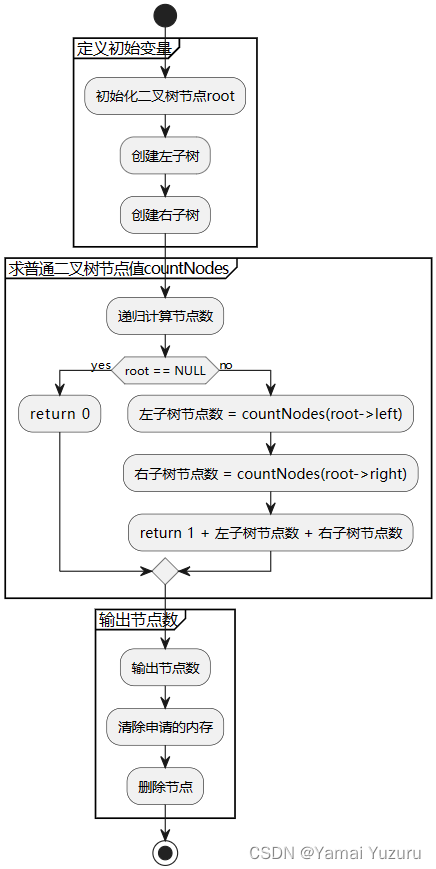
        当求任意一棵二叉树的节点个数时，可以使用递归的方式来解决。下面是一种求二叉树节点个数的思路和题解：

1. 如果根节点为空，则树中没有节点，返回节点个数为0。
2. 否则，递归计算根节点的左子树的节点个数，记为 leftCount。
3. 递归计算根节点的右子树的节点个数，记为 rightCount。
4. 节点个数等于左子树节点个数、右子树节点个数和根节点本身的总和（即 leftCount + rightCount + 1）。
5. 返回节点个数作为结果。

示例

        直接用了之前的输入（普通也包含完全）。

1. 要计算整个树的节点个数，开始于根节点1。
2. 根节点1本身是一个节点，因此开始时计数为1。
3. 接下来，递归地计算节点2的子树节点个数。节点2有两个孩子，节点4和节点5，它们都没有孩子，所以子树2的节点个数是1（节点2本身）+1（节点4）+1（节点5）=3。
4. 同样，节点3也被递归地计算。节点3有一个孩子，节点6，它没有孩子，所以节点3的子树节点个数是1（节点3本身）+1（节点6）=2。
5. 将所有计数相加：1（根节点1）+3（节点2及其子树的节点数）+2（节点3及其子树的节点数）=6。

        所以最终，整棵树的节点个数为6。

        这个过程是通过代码中的递归函数countNodes实现的。函数countNodes按照上述逻辑，以树的根节点开始访问每个节点，并递归地遍历它们的左右子树，计算每个子树的节点数，并将它们与当前节点的数量（1）相加。当遇到空子树（即NULL，或没有子节点的节点）时，递归调用返回0，表示这里没有更多的节点需要计数。通过这种方式，所有节点被计数并求和，得到整棵树的节点总数。   

梳理

        普通二叉树和完全二叉树在结构上存在显著不同，因此求解它们节点个数的最佳方法往往也不同。这些不同主要表现在：

1. 普通二叉树：它的结构没有特定的规则，节点可以任意地分布在左右子树中。为了计算普通二叉树中的节点数，我们通常采用递归方法，对每个节点进行遍历。递归过程中，当遇到一个非空节点时，就将计数加1，并继续递归计算它的左右子节点。

2. 完全二叉树：它是一种特殊的二叉树，所有的层都是满的，除了最后一层，最后一层的节点尽量都向左排列。这种结构使得我们可以利用完全二叉树的性质来用非递归的方法来计算节点数。例如，可以通过计算树高以及最后一层节点的数量来求得总节点数。因为在完全二叉树中，除了最后一层外，其余每层的节点数都是已知的（即 2^层级数 - 1）。

        可以使用普通二叉树计算节点个数的方法来计算完全二叉树的节点数，即递归遍历每个节点，这种方法在任何类型的二叉树中都适用。然而，当树的高度较大时，这种方法相对较慢，因为它需要访问树中的每个节点。

        针对完全二叉树，利用其特殊性质（每层节点数等比递增、最后一层节点尽量左对齐等），可以设计出更为高效的算法（其他方法回头补）。

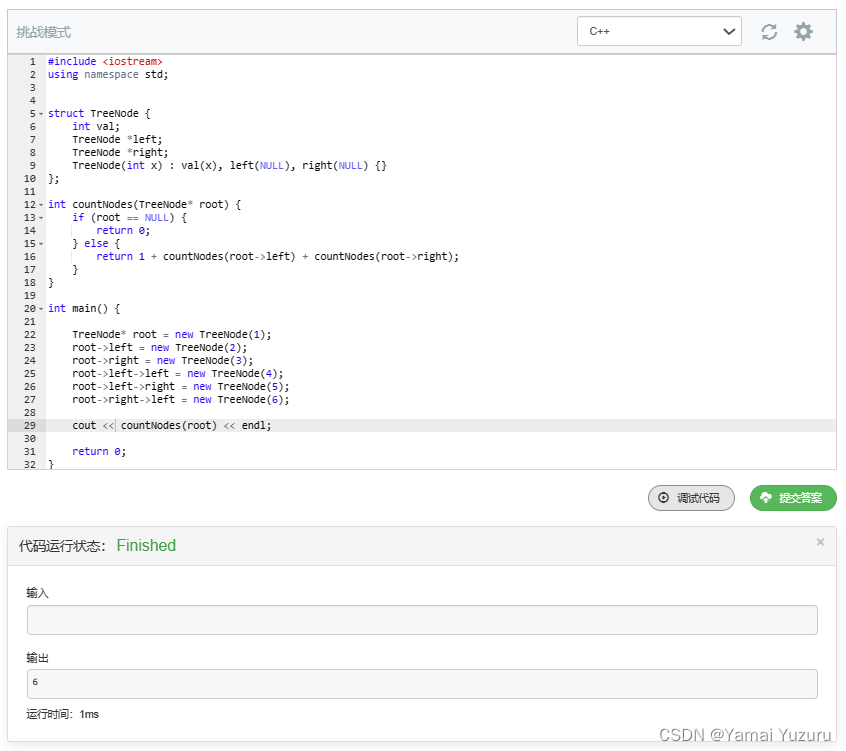
代码

#include <iostream>
using namespace std;// 定义二叉树节点结构体
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};// 用于计算二叉树节点数的递归函数
int countNodes(TreeNode* root) {if (root == NULL) {return 0;} else {return 1 + countNodes(root->left) + countNodes(root->right);}
}// 主函数
int main() {// 创建二叉树// 注意：这里仅作为示例，具体创建二叉树的方法取决于输入格式和树结构TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);root->right->left = new TreeNode(6);// 计算节点数并输出结果cout << "Number of nodes: " << countNodes(root) << endl;// 清理申请的内存(此处未显示，但在实际使用中需要处理)// 如通过后序遍历删除所有节点// deleteTree(root);return 0;
}

打卡