引言
计算一个正整数的阶乘是常见的数学问题。阶乘的定义为:n的阶乘(记作n!)是所有小于及等于n的正整数的乘积。例如,5的阶乘(5!)就是5×4×3×2×1=120。下面我们将通过一个使用递归方法实现阶乘的C语言代码示例,并进一步探讨如何采用非递归(迭代)的方式来实现相同的功能。
递归实现
int PAND_recursive(int a) {if (a == 0){return 1; // 阶乘的递归基}return a * PAND_recursive(a - 1); // 递归调用
} 递归方法的核心在于将复杂问题简化为相似的子问题。在上述代码中,PAND_recursive函数通过递归地调用自身,每次将待求解的阶乘问题转换为较小的阶乘问题,直至达到递归基(即a=0),此时直接返回1。
图解
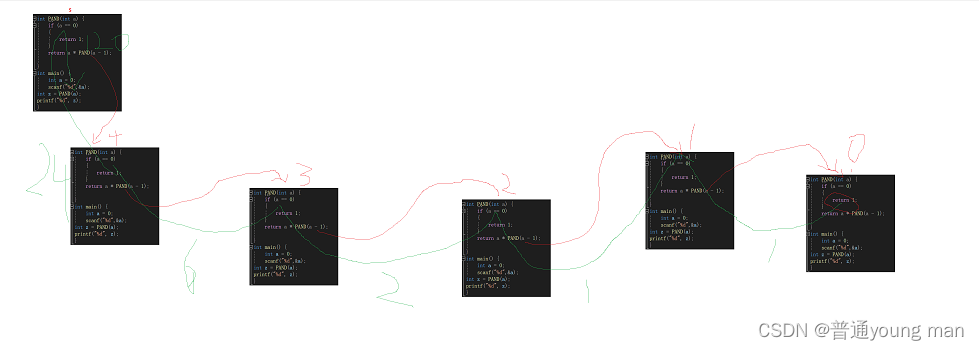
红:递推 绿:回归
迭代实现
int PAND_iterative(int a) {int factorial = 1;for(int i = 1; i <= a; ++i) {factorial *= i;}return factorial;
} 在PAND_iterative函数中,我们使用了一个for循环,从1开始,逐步将每个整数乘以累计变量factorial,直至遍历到输入值a,从而实现阶乘的计算。
主函数
int main() {int a = 0;scanf("%d",&a);// 使用递归方法计算阶乘int recursive_result = PAND_recursive(a);// 使用迭代方法计算阶乘int iterative_result = PAND_iterative(a);// 输出结果(这里仅以迭代结果为例)printf(" %d\n", a, iterative_result);return 0;
}递归与迭代方法的优缺点对比
-
递归方法的优点在于逻辑表达简洁清晰,尤其适合描述和解决具有自然递归性质的问题。缺点是对于大数值阶乘计算,递归调用可能导致栈溢出,且相对迭代方法效率较低。
-
迭代方法则通过循环结构逐步解决问题,不需要额外的函数调用,减少了栈空间的消耗,且在效率上优于递归方法。但相对于递归,其逻辑可能稍显复杂,尤其是对于初学者而言,理解起来可能需要更多的时间和练习。
综上所述,针对阶乘计算这样的问题,开发者可以根据实际情况和需求,灵活选择递归或迭代这两种不同的实现策略。


 | Ei Scopus检索)







)








