- 小结
- 博弈论题型
- 素数的特性
- 连续异或
- 代码
题目:素数取りゲーム
临摹的题解:AT_ttpc2019d题解
这题真的看题解都断断续续看了两天才看懂这一个题解 : (
小结
本题一下遇到了我好多没了解过的点,博弈论、素数的一些特性,连续异或的本质
下文部分包含参考题解的情景下的用词
博弈论题型
- 取东西取尽结算胜负的博弈,都是剩余 相同类型的操作(本题对应贡献为1、2、3的三类)有偶数步数时,后手赢 ,因为后手直接克隆先手操作就稳赢了
- 由1.可得:分析此种博弈,从后手必胜的情况入手 比较简单,可以 剔除掉偶数部分去推演 ,奇数项留1个,就可以作所有情况的最终基本情况了
举例:(1、2、3表示贡献度)
奇数个1,奇数个2,奇数个3 ==> 1个1,1个2,1个3
上面两个是等效的,因为后手可以copy前面取其他1、2、3的所有操作
这其实刚好是参考题解中,贡献度异或为0情况时最复杂的情况的“最终基本情况”
- 先手必胜的情况,就是后手必输的情况!两种情况其实都是一种情况,“必输就是必胜!”
举例:(先手A,后手B,以先手必胜的情况开局) A走一步之后,此时A就是此时战况的后手了,而A仍然是是必胜的! 那不就是走一步后转化为后手的必胜情况了?
素数的特性
参考题解里解释的非常清楚。
连续异或
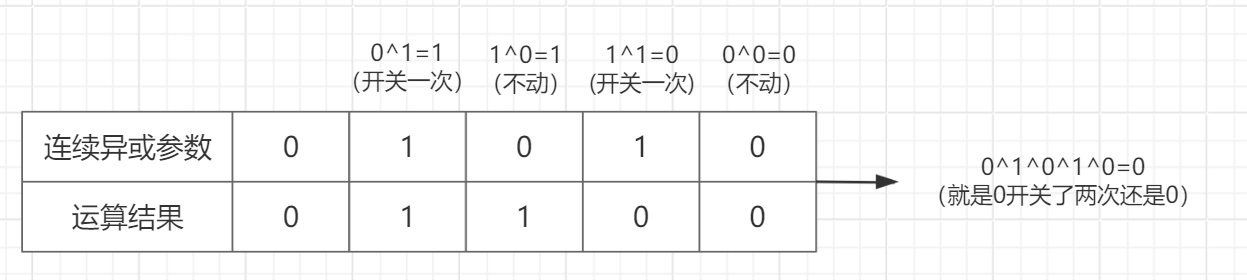
连续异或的作用:可以将其看作以“关”为起点(或者以第一个参与运算的值为起点,一样的),遇到1则开关一次,遇到0则不动的一个流程
结果就是偶数个1最终是“关”,也就是0,奇数个1就是“开”,也就是1
代码
#include <iostream>
#include <bitset>
using namespace std;
#define FIRST "An"
#define LAST "Ai"
//数组长度范围2ee5,素数范围1e6const int N = 1e6 + 5;
bitset<N> mark; //注意!!!mark[i]==0 时才是素数
int primes[N/10]; //不需要那么大
int n;
int cnt = 0;int main()
{mark[0] = mark[1] = 1; //mark[i]==0 时才是素数,所以0、1不是素数要标记//先初始化素数数据库,线性筛for (int i = 2; i <= N; i++){if(!mark[i]) primes[++cnt] = i;for (int j = 1; primes[j] <= N /i; j++){mark[primes[j] * i] = 1;if(i%primes[j] == 0) break;}}cin >> n;int num;int res = 0;for (int i = 1; i <= n; i++){cin >> num;if(mark[num-2] == 0)//如果-2是素数,那么一定>=5,先这样判断以避免越界,因为题目要求X>=2,而2-4<0{if(num ==7)res ^= 3;elseres ^= 2;}elseres ^= 1;}switch (res){case 0:cout << LAST; //后手必胜break;default:cout << FIRST;break;}
}








——详解】)

)






