数学建模--G(1,1)型的灰色预测模型的Python实现

1.算法适用情况

2.算法推演步骤

3.算法核心代码

4.算法效果展示

1.算法适用情况

#1.灰色预测模型简介
"""
1.灰色预测是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
2.灰色预测对原始数据进行生成处理来寻找系统变动的规律，并生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。
3.灰色预测模型要求时长尽可能多或者数据尽可能充足,如果数据不足的话灰色预测的效果很差
4.如果数据不足,可以采用普通的时间序列来进行预测
"""

2.算法推演步骤

#算法步骤如下所示:
#1.生成累加数据集合
#2.计算矩阵B和向量Y
#3.计算结果矩阵U=[a,u] U=(B^T.B)^-1.B^T.Y
#4.建立灰色预测模型函数
#5.灰色预测精度检验
#6.灰色误差检验
#7.可视化绘图

3.算法核心代码

#1.灰色预测模型简介
"""
1.灰色预测是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
2.灰色预测对原始数据进行生成处理来寻找系统变动的规律，并生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。
3.灰色预测模型要求时长尽可能多或者数据尽可能充足,如果数据不足的话灰色预测的效果很差
4.如果数据不足,可以采用普通的时间序列来进行预测
"""
#导入必要的库和数据
import math
import numpy as np
import matplotlib.pyplot as plt
# 这两行代码解决 plt 中文显示的问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falsehist_data=[724.57,746.62,778.27,800.8,827.75,871.1,912.37,954.28,995.01,1037.2]
number=len(hist_data)
x0=np.array(hist_data)#1.生成累加数据集合
add_hist_data = [sum(hist_data[0:i+1]) for i in range(number)]
x1 = np.array(add_hist_data)
#2.计算矩阵B和向量Y
#B矩阵是一个number-1行2列的矩阵
#Y向量是一个number-1行1列的矩阵
B=np.zeros([number-1,2])
Y=np.zeros([number-1,1])
#通过for循环计算值
#Y=[x0[1],x0[2],x0[3],.......x0[n-1]]
#B=[[-0.5(x(0)+x(1)),1],.......,[-0.5(x(number)+x(1=number-1)),1]]
for i in range(0,number-1):B[i][0] = -0.5*(x1[i] + x1[i+1])B[i][1] = 1Y[i][0] = x0[i+1]
#3.计算结果矩阵U=[a,u]^T
#U=(B^T.B)^-1.B^T.Y
U=np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
a=U[0][0]
u=U[1][0]
#4.建立灰色预测模型函数
ans=np.zeros(number)
ans[0]=x0[0]
for i in range(1,number):ans[i]=(x0[0]-u/a)*(1-math.exp(a))*math.exp(-a*(i))
#5.灰色预测精度检验
#5.1.残差平均值+残差平方
#残差平均值
aver0=0
for i in range(number):aver0+=(x0[i]-ans[i])
aver0=aver0/number
#残差平方
s0 = 0;       
for i in range(0,number):s0 += ((x0[i] - ans[i]) - aver0)**2;
s0 /= number#5.2.历史数据平均值+历史数据方差
aver1=0
S1=0
for i in range(number):aver1+=(x0[i])
aver1=aver1/number
for i in range(number):S1+= (x0[i]-aver1)**2;
S1 /= number
#5.3.后验差比值
C=s0/S1
#5.4.小误差概率P
sum=0
for i in range(number):if abs(x0[i]-ans[i]-aver0)<0.6754*math.sqrt(S1):sum=sum+1else:sum=sum
p=sum/number
#6.灰色误差检验
ANS=0
if(C<0.35 and p>0.95):#预测效果不错ANS=1m=20answer=np.zeros(m)for i in range(m):answer[i]=(x0[0]-u/a)*(1-math.exp(a))*math.exp(-a*(i+number))
else:ANS=0print("关联性不强,灰色预测法不可用!")
#7.可视化绘图
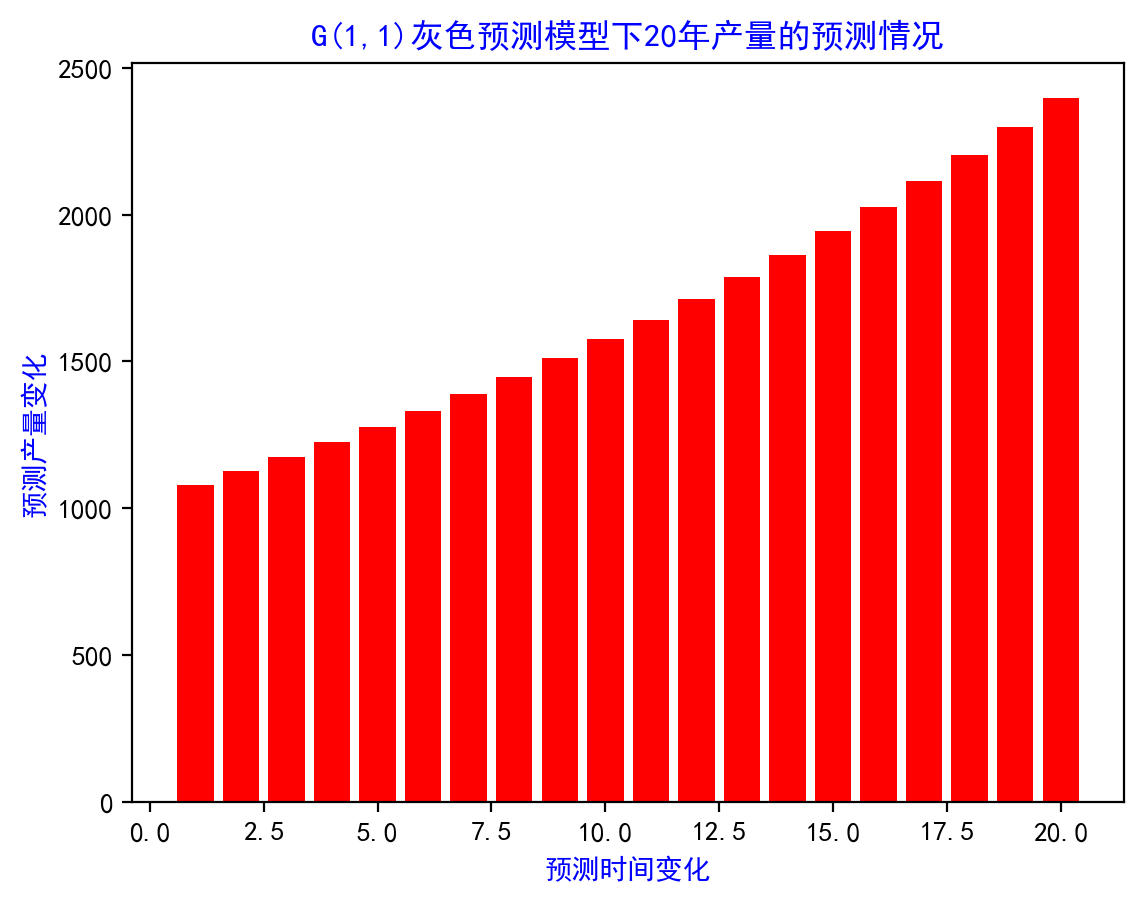
if ANS == 1:for i in range(m):print("预测第",i+1,"年的数据是:",answer[i])x=[]y=[]for i in range(m):x.append(i+1)y.append(answer[i]) plt.bar(x,y,color='r')plt.xlabel("预测时间变化",color='b')plt.ylabel("预测产量变化",color='b')plt.title("G(1,1)灰色预测模型下20年产量的预测情况",color='b')plt.savefig('C:/Users/Zeng Zhong Yan/Desktop/灰度预测模型.png', dpi=200, bbox_inches='tight')plt.show()