介绍
随机森林是一种基于集成学习的有监督机器学习算法。随机森林是包含多个决策树的分类器,一般输出的类别是由决策树的众数决定。随机森林也可以用于常见的回归拟合。随机森林主要是运用了两种思想。具体如下所示。
- Breimans的Bootstrap aggregating
- Ho的random subspace method
储备知识
集成学习
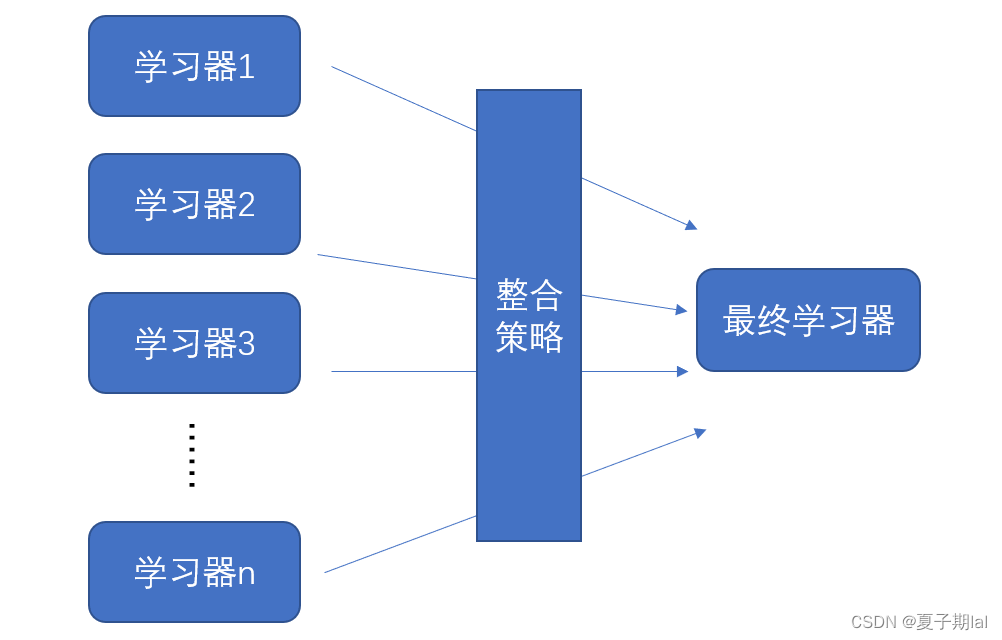
集成学习主要是通过个体学习器(如决策树)通过一定组合策略将其组合起来,形成一个准确率较高,较为优秀的学习器。
学习器有同质和异质之分,如随机森林里面的学习器都是决策树,即为是同质,反之即为异质。
集成学习的学习器一般为弱学习器,但弱学习器也需要下列特质。
- 需要一定的准确性
- 需要多样性,弱学习器之间需要存在一定差异性
决策树学习
决策树是机器学习常见的方法,而且决策树本质为树学习,树学习能够有以下优点。
- 在特征值缩放和其他转换下,决策树的结果保持不变
- 无关特征对于结果影响较少,因此决策树对于无关结果是稳健的
树学习的缺点如下。
- 生长很深的树容易学习到高度不规则的模式,即为过学习,在训练集上具有一定的低偏差和高变异数的特点。
因此,随机森林是平均多个深决策树的结果,目的是为了降低变异数。此外,随机森林的决策树是在一个数据集的不同部分进行训练,各部分具有一定的独立性。
随机森林的缺点为偏差的小幅增加和可解释性的丧失。优点为用于大数据集上能够提高准确率和性能。
Bagging 算法
Bagging算法又称为引导聚集算法(装袋算法),属于集成学习算法。主要的目的为能够提高回归,风雷的准确性以及稳定性,同时能够降低结果的变异数,降低过拟合发生的概率。
随机森林训练算法将bagging算法应用于树学习中,给定训练集合 X = x 1 , ⋯ x n X=x_1, \cdots x_n X=x1,⋯xn和label集合 Y = y 1 ⋯ y n Y=y_1 \cdots y_n Y=y1⋯yn,Bagging 算法会从训练集合中有放回采样B次,在这些样本上不断训练树模型。
具体流程如下所示。
For b = 1, …, B:(循环B次,即为重复B次操作)
Sample, with replacement, n training examples from X, Y; call these Xb, Yb.(有放回采样,样本数量为B)
Train a classification or regression tree fb on Xb, Yb(训练树回归/分类模型)
迭代B次之后即为训练结束,对未知样本x的预测可以通过对x上所有单个回归书的预测求取平均来实现。
公式如下所示。 f ^ \hat f f^为预测结果,可以为分类或者拟合结果。 f b ( x ′ ) f_b(x^{\prime}) fb(x′)为经过单个决策树之后的结果。
f ^ = 1 B ∑ b = 1 B f b ( x ′ ) \hat{f}=\frac1B\sum_{b=1}^Bf_b(x^{\prime}) f^=B1b=1∑Bfb(x′)
此外, x ′ x^{\prime} x′上所以单个回归树的预测的标准差可以作为预测的不确定性的估计数值。具体公式如下所示。
σ = ∑ b = 1 B ( f b ( x ′ ) − f ^ ) 2 B − 1 . \sigma=\sqrt{\frac{\sum_{b=1}^B(f_b(x^{\prime})-\hat{f})^2}{B-1}}. σ=B−1∑b=1B(fb(x′)−f^)2.
bagging方法在不增加偏置的情况下能够降低方差。
单个树模型的预测会对数据集的噪声十分敏感,因此对于多个树模型,只要树模型没有明显的相关性,在同一个数据集上简单的训练多个树模型会导致树模型具有强相关性。因此bagging方法的Bootstrap抽样方法能够通过同样的数据集产生不同的训练集以供其他树模型训练。从而降低模型的关联性。
代码
样本数据主要根据下列连接获取。
需要自主上传下载google云盘去获取
import sklearn.datasets as datasets
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestRegressor
from sklearn.decomposition import PCA
from six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
import os# 导入数据,路径中要么用\\或/或者在路径前加r,目前是读取当前路径,所以数据文件要放置在同一文件夹/目录中
dataset = pd.read_csv(r'./petrol_consumption.csv')# 准备训练数据
# 自变量, 因变量,本代码主要做的是拟合,而且这里主要获取数据的dataframe转化为ndarry
X = dataset.iloc[:, 0:4].values
y = dataset.iloc[:, 4].values# 将数据分为训练集和测试集,切分数据集合,而且比例为8:2,随机种子为0,保证结果可复现性
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=0)
regr = RandomForestRegressor() # 设置随机森林拟合,下列为参数
# regr = RandomForestRegressor(random_state=100,
# bootstrap=True,
# max_depth=2,
# max_features=2,
# min_samples_leaf=3,
# min_samples_split=5,
# n_estimators=3)
# 这里为封装管道,最终直接可以调用,所以这里运用的是最大最小归一化,而且运用的是PCA降低维度,最终回归用的是regr,所以走完了所有的操作
pipe = Pipeline([('scaler', StandardScaler()), ('reduce_dim', PCA()),('regressor', regr)])
pipe.fit(X_train, y_train)
ypipe = pipe.predict(X_test)# 执行一次,需要自己去配置graphviz,这个网上有很多教程,主要是用于绘制图像
# os.environ['PATH'] = os.environ['PATH']+';'+r"D:\CLibrary\Graphviz2.44.1\bin\graphviz"
dot_data = StringIO()
# export_graphviz()数是一个用于将决策树可视化的函数,通常与机器学习库scikit-learn一起使用
export_graphviz(pipe.named_steps['regressor'].estimators_[0],# pipe.named_steps['regressor'].estimators_[0]返回的是回归器的第一个实例,即为随机初始化一个决策树绘制out_file=dot_data)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('tree.png')Image(graph.create_png())# Get numerical feature importances,获取特征(输入变量的重要程度,即为判断哪个因素最为重要)
importances = list(regr.feature_importances_)
# List of tuples with variable and importance
print(importances)# 保存模型的特征名称
feature_list = list(dataset.columns)[0:4]
# round()函数将特征重要程度四舍五入
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(feature_list, importances)]
# 将特征重要程度进行排序
feature_importances = sorted(feature_importances, key = lambda x: x[1], reverse = True)import matplotlib.pyplot as plt
# Set the style
# plt.style.use('fivethirtyeight')
# list of x locations for plotting
x_values = list(range(len(importances)))
print(x_values)
# Make a bar chart
plt.bar(x_values, importances, orientation = 'vertical')
# Tick labels for x axis
plt.xticks(x_values, feature_list,rotation=6)
# Axis labels and title
plt.ylabel('Importance'); plt.xlabel('Variable'); plt.title('Variable Importances');
plt.show()
print('successful')
回归器的参数如下所示。sklearn的RandomForestRegressor参数如下所示。
'''
sklearn.ensemble.RandomForestRegressor(
n_estimators=100, *, # 树的棵树,默认是100
criterion='mse', # 默认“ mse”,衡量质量的功能,可选择“mae”。
max_depth=None, # 树的最大深度。
min_samples_split=2, # 拆分内部节点所需的最少样本数:
min_samples_leaf=1, # 在叶节点处需要的最小样本数。
min_weight_fraction_leaf=0.0, # 在所有叶节点处的权重总和中的最小加权分数。
max_features='auto', # 寻找最佳分割时要考虑的特征数量。
max_leaf_nodes=None, # 以最佳优先方式生长具有max_leaf_nodes的树。
min_impurity_decrease=0.0, # 如果节点分裂会导致杂质的减少大于或等于该值,则该节点将被分裂。
min_impurity_split=None, # 提前停止树木生长的阈值。
bootstrap=True, # 建立树木时是否使用bootstrap抽样。 如果为False,则将整个数据集用于构建每棵决策树。
oob_score=False, # 是否使用out-of-bag样本估算未过滤的数据的R2。
n_jobs=None, # 并行运行的Job数目。
random_state=None, # 控制构建树时样本的随机抽样
verbose=0, # 在拟合和预测时控制详细程度。
warm_start=False, # 设置为True时,重复使用上一个解决方案,否则,只需拟合一个全新的森林。
ccp_alpha=0.0,
max_samples=None) # 如果bootstrap为True,则从X抽取以训练每个决策树。
'''
参考
维基百科随机森林介绍
随机森林算法梳理(Random Forest)
一文看懂随机森林
用Python实现随机森林回归




大数据实战——Flume数据采集的基本案例实战)


)
![[FFmpeg] 常用ffmpeg命令](http://pic.xiahunao.cn/[FFmpeg] 常用ffmpeg命令)









及其应用:青蛙跳台阶问题)
