98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

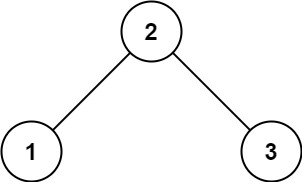
输入：root = [2,1,3]
输出：true

示例 2：

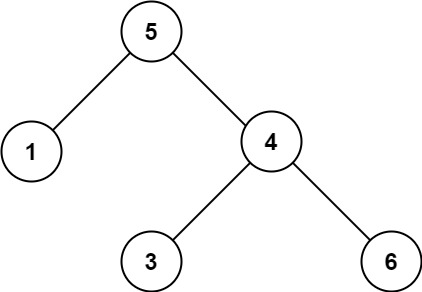
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路：要验证肯定要遍历，想到如果符合二叉搜索树的话，中序遍历的结果就会是从小到大的，判断一下即可。若需要判断，那么需要加上一个临时结点来记录上一个遍历的结点。

代码实现：

class Solution {
public:bool isValidBST(TreeNode* root) {stack<TreeNode *> stk;TreeNode *cur = root;TreeNode *pre = nullptr;while(cur || !stk.empty()) {if(cur) {stk.push(cur);cur = cur->left;}else {cur = stk.top();stk.pop();if(pre && cur->val <= pre->val) return false;pre = cur;cur = cur->right;}}return true;}
};

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

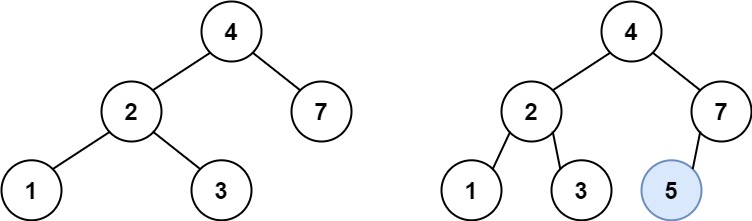
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

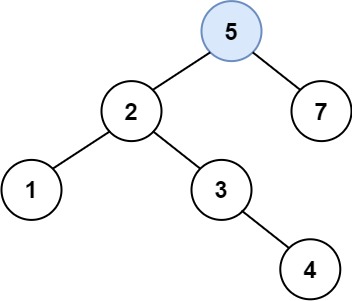
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

思路：想了想，要是重构二叉树好像有些复杂，这样的话，始终添加为叶子结点就好。那么，还是会用到两个结点，一个cur用于遍历和判断，另一个pre用于在判断找到叶子结点后，再判断添加为左孩子（新节点小）还是右孩子（新节点大）。

代码实现：

class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root == nullptr) {TreeNode *node = new TreeNode(val);return node;}TreeNode *cur = root;TreeNode *pre = nullptr;while(cur) {pre = cur;if(cur->val > val) cur = cur->left;else if(cur->val <= val) cur = cur->right;}TreeNode *node = new TreeNode(val);if(pre->val > val) pre->left = node;else if(pre->val <= val) pre->right = node;return root;}
};