whale-quant 学习 part7：量化回测

量化回测

计算策略评估指标
聚宽平台量化回测实践
- 策略实现
参考

计算策略评估指标

使用数据为：贵州茅台（600519.SH）、工商银行（601398.SH）、中国平安（601318.SH），策略基准是沪深300指数（000300.XSHG），策略采用最简单的方式：买入持有。持有周期为20180101 - 20221231，共1826个自然日。
数据获取

import pandas as pd  
import numpy as np
import matplotlib.pyplot as plt
import tushare as ts
%matplotlib inline   # 无视warning
import warnings
warnings.filterwarnings("ignore")# 正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False#起始和结束日期可以自行输入，否则使用默认
def get_data(code, start_date, end_date):# 配置 tushare tokenmy_token = 'XXXXX'  pro = ts.pro_api(my_token)df = pro.daily(ts_code=code, start_date=start_date, end_date=end_date)df.index = pd.to_datetime(df.trade_date)return df.close#以上证综指、贵州茅台、工商银行、中国平安为例
stocks={'600519.SH':'贵州茅台','601398.SH':'工商银行','601318.SH':'中国平安'
}df = pd.DataFrame()
for code,name in stocks.items():df[name] = get_data(code, '20180101', '20221231')# 按照日期正序
df = df.sort_index()# 本地读入沪深300合并
df_base = pd.read_csv('000300.XSHG_2018_2022.csv')
df_base.index = pd.to_datetime(df_base.trade_date)
df['沪深300'] = df_base['close']

净值曲线 一组时间序列的曲线，其含义表示为股票或基金在不同时间的价值相对于期初的价值的倍数。

# 以第一交易日2018年1月1日收盘价为基点，计算净值并绘制净值曲线
df_worth = df / df.iloc[0]
df_worth.plot(figsize=(15,6))
plt.title('股价净值走势', fontsize=10)
plt.xticks(pd.date_range('20180101','20221231',freq='Y'),fontsize=10)
plt.show()

年化收益率
累计收益率
$R_t = \frac{P_r-P_t}{P_t} \\ P_T 表示在期末资产的价格 \\ P_t 表示期初资产价格$
年化收益率
$R_p = (1+R)^{\frac{m}{n}}-1$
R表示期间总收益率，m是与n(可以是天数、周数、月数)相对应的计算周期，根据计算惯例，m=252、52、12分别指代日、周、月向年化的转换；n为期间自然日天数。(年化收益的一个直观的理解是，假设按照某种盈利能力，换算成一年的收益大概能有多少。这个概念常常会存在误导性，比如，这个月股票赚了5%，在随机波动的市场中，这是很正常的现象。如果据此号称年化收益为5%×12个月=60%，这就显得不太可信了，实际上每个月的收益不可能都这么稳定。所以在听到有人说年化收益的时候，需要特别留意一下具体的情况，否则很容易被误导。)

# 区间累计收益率(绝对收益率)
total_return = df_worth.iloc[-1]-1
total_return = pd.DataFrame(total_return.values,columns=['累计收益率'],index=total_return.index)
total_return# 年化收益率
annual_return = pd.DataFrame((1 + total_return.values) ** (252 / 1826) - 1,columns=['年化收益率'],index=total_return.index)
annual_return

波动率
波动率是对收益变动的一种衡量，本质也是风险，波动率和风险，都是用来衡量收益率的不确定性的。我们用方差来表示，年波动率等于策略收益和无风险收益的标准差除以其均值，再除以交易日倒数的平方根，通常交易日取252天。
$\sqrt{\frac{252}{n-1}\sum^{n}_{ri=1}(r_p-\hat{r_p})^2} \\ r_p 表示策略每日收益率 \\ \hat{r_p} 表示策略每日收益率的平均值 \\ n表示策略执行天数$

df_return = df / df.shift(1) - 1
df_return = ((df_return.iloc[1:] - df_return.mean()) ** 2)volatility = pd.DataFrame(np.sqrt(df_return.sum() * 252 / (1826-1)),columns=['波动率'],index=total_return.index)
volatility

最大撤回
选定周期内任一历史时点往后推，于最低点时的收益率回撤幅度的最大值。最大回撤用来描述可能出现的最糟糕的情况。最大回撤是一个重要的风险指标，对于量化策略交易，该指标比波动率还重要。 P为某一天的净值，i为某一天，j为i后的某一天，Pi为第i天的产品净值，Pj则是Pi后面某一天的净值
该资产的最大回撤计算如下：
$MaxDrawdown=\frac{max(P_i-P_j)}{P_i}$

def max_drawdown_cal(df):md = ((df.cummax() - df)/df.cummax()).max()return round(md, 4)max_drawdown = {}stocks={'600519.SH':'贵州茅台','601398.SH':'工商银行','601318.SH':'中国平安','000300.XSHG': '沪深300'
}for code,name in stocks.items():max_drawdown[name]=max_drawdown_cal(df[name])max_drawdown = pd.DataFrame(max_drawdown,index=['最大回撤']).T
max_drawdown

Alpha和Beta系数
Beta系数代表投资中的系统风险，而在投资中除了系统风险外还面临着市场波动无关的非系统性风险。 Alpha系数就代表投资中的非系统性风险，是投资者获得与市场波动无关的回报。
可以使用资本资产定价模型（CAPM）来估计策略的beta和alpha值，CAPM模型为：
$E(r_i)=r_f+\beta(E(r_m)-r_f) \\ E(r_i) 表示投资组合的预期收益率 \\ r_f 表示无风险利率 \\ r_m 表示市场指数收益率 \\ \beta 表示股市波动风险与投资机会中的结构性与系统性风险 \\ CAPM的计量模型可以表示为 \\ r_i=\alpha+\beta r_m +\epsilon_{\alpha} \\ \epsilon_\alpha表示随机扰动，即个体风险$

from scipy import stats#计算每日收益率 收盘价缺失值（停牌），使用前值代替
rets=(df.iloc[:,:4].fillna(method='pad')).apply(lambda x:x/x.shift(1)-1)[1:]#市场指数为x，个股收益率为y
x = rets.iloc[:,3].values
y = rets.iloc[:,:3].values
capm = pd.DataFrame()
alpha = []
beta = []
for i in range(3):b, a, r_value, p_value, std_err=stats.linregress(x,y[:,i])#alpha转化为年化alpha.append(round(a*250,3))beta.append(round(b,3))capm['alpha']=alpha
capm['beta']=beta
capm.index=rets.columns[:3]
#输出结果：
capm

夏普比率
夏普比率（sharpe ratio）表示每承受一单位总风险，会产生多少的超额报酬，该比率越高。夏普比率是在资本资产定价模型进一步发展得来的。
$SharpeRatio=\frac{R_p-R_f}{\sigma_p} \\R_p 表示策略年化收益率 \\R_F 表示无风险收益差 \\ \sigma_p表示年化标准差$

# 超额收益率以无风险收益率为基准 假设无风险收益率为年化3%
ex_return=rets - 0.03/250# 计算夏普比率
sharpe_ratio=np.sqrt(len(ex_return))*ex_return.mean()/ex_return.std()
sharpe_ratio=pd.DataFrame(sharpe_ratio,columns=['夏普比率'])
sharpe_ratio

信息比率
信息比率含义与夏普比率类似，只不过其参照基准不是无风险收益率，而是策略的市场基准收益率。
$InformationRatio=\frac{R_p-R_f}{\sigma_t} \\ R_p 表示策略年化收益率 \\ R_F表示无风险收益率 \\ \sigma_t 表示策略与基准每日收益率差值的年化标准差$

###信息比率
ex_return = pd.DataFrame() 
ex_return['贵州茅台']=rets.iloc[:,0]-rets.iloc[:,3]
ex_return['工商银行']=rets.iloc[:,1]-rets.iloc[:,3]
ex_return['中国平安']=rets.iloc[:,2]-rets.iloc[:,3]#计算信息比率
information_ratio = np.sqrt(len(ex_return))*ex_return.mean()/ex_return.std()
#信息比率的输出结果
information_ratio = pd.DataFrame(information_ratio,columns=['信息比率'])
information_ratio

聚宽平台量化回测实践

聚宽（https://www.joinquant.com/）成立于2015年5月，是一家量化交易平台，为投资者提供做量化交易的工具与服务，帮助投资者更好地做量化交易。整体来看，聚宽具有以下几点优势

聚宽让做量化交易的成本极大降低
提供多种优质的便于取用的数据
提供投资研究功能，便于自由地统计、研究、学习等
提供多种的策略评价指标与评价维度
支持多种策略的编写、回测、模拟、实盘
具备丰富且活跃的量化社区，可以发帖、学习、比赛等。

策略实现

本部分将介绍如何在聚宽平台实现一个双均线策略（具体参照ch05择时策略），并且在聚宽平台上进行回测，来测试整体收益率。

策略代码如下，核心点有：

选择标的为：002594.XSHE 比亚迪
选择基准为：000300.XSHG 沪深300
策略为：当5日线金叉10日线，全仓买入；当5日线死叉10日线全仓卖出。

# 导入函数库
from jqdata import *# 初始化函数，设定基准等等
def initialize(context):# 设定沪深上证作为基准set_benchmark('000300.XSHG')# 开启动态复权模式(真实价格)set_option('use_real_price', True)# 输出内容到日志 log.info()log.info('初始函数开始运行且全局只运行一次')# 过滤掉order系列API产生的比error级别低的log# log.set_level('order', 'error')### 股票相关设定 #### 股票类每笔交易时的手续费是：买入时佣金万分之三，卖出时佣金万分之三加千分之一印花税, 每笔交易佣金最低扣5块钱set_order_cost(OrderCost(close_tax=0.001, open_commission=0.0003, close_commission=0.0003, min_commission=5), type='stock')## 运行函数（reference_security为运行时间的参考标的；传入的标的只做种类区分，因此传入'000300.XSHG'或'510300.XSHG'是一样的）# 开盘前运行run_daily(before_market_open, time='before_open', reference_security='000300.XSHG')# 开盘时运行run_daily(market_open, time='open', reference_security='000300.XSHG')# 收盘后运行run_daily(after_market_close, time='after_close', reference_security='000300.XSHG')## 开盘前运行函数
def before_market_open(context):# 输出运行时间log.info('函数运行时间(before_market_open)：'+str(context.current_dt.time()))# 给微信发送消息（添加模拟交易，并绑定微信生效）# send_message('美好的一天~')# 要操作的股票：比亚迪（g.为全局变量）g.security = '002594.XSHE'## 开盘时运行函数
def market_open(context):log.info('函数运行时间(market_open):'+str(context.current_dt.time()))security = g.security# 获取股票的收盘价close_data5 = get_bars(security, count=5, unit='1d', fields=['close'])close_data10 = get_bars(security, count=10, unit='1d', fields=['close'])# close_data20 = get_bars(security, count=20, unit='1d', fields=['close'])# 取得过去五天，十天的平均价格MA5 = close_data5['close'].mean()MA10 = close_data10['close'].mean()# 取得上一时间点价格#current_price = close_data['close'][-1]# 取得当前的现金cash = context.portfolio.available_cash# 五日均线上穿十日均线if (MA5 > MA10) and (cash > 0):# 记录这次买入log.info("5日线金叉10日线，买入 %s" % (security))# 用所有 cash 买入股票order_value(security, cash)# 五日均线跌破十日均线elif (MA5 < MA10) and context.portfolio.positions[security].closeable_amount > 0:# 记录这次卖出log.info("5日线死叉10日线, 卖出 %s" % (security))# 卖出所有股票,使这只股票的最终持有量为0for security in context.portfolio.positions.keys():order_target(security, 0)## 收盘后运行函数
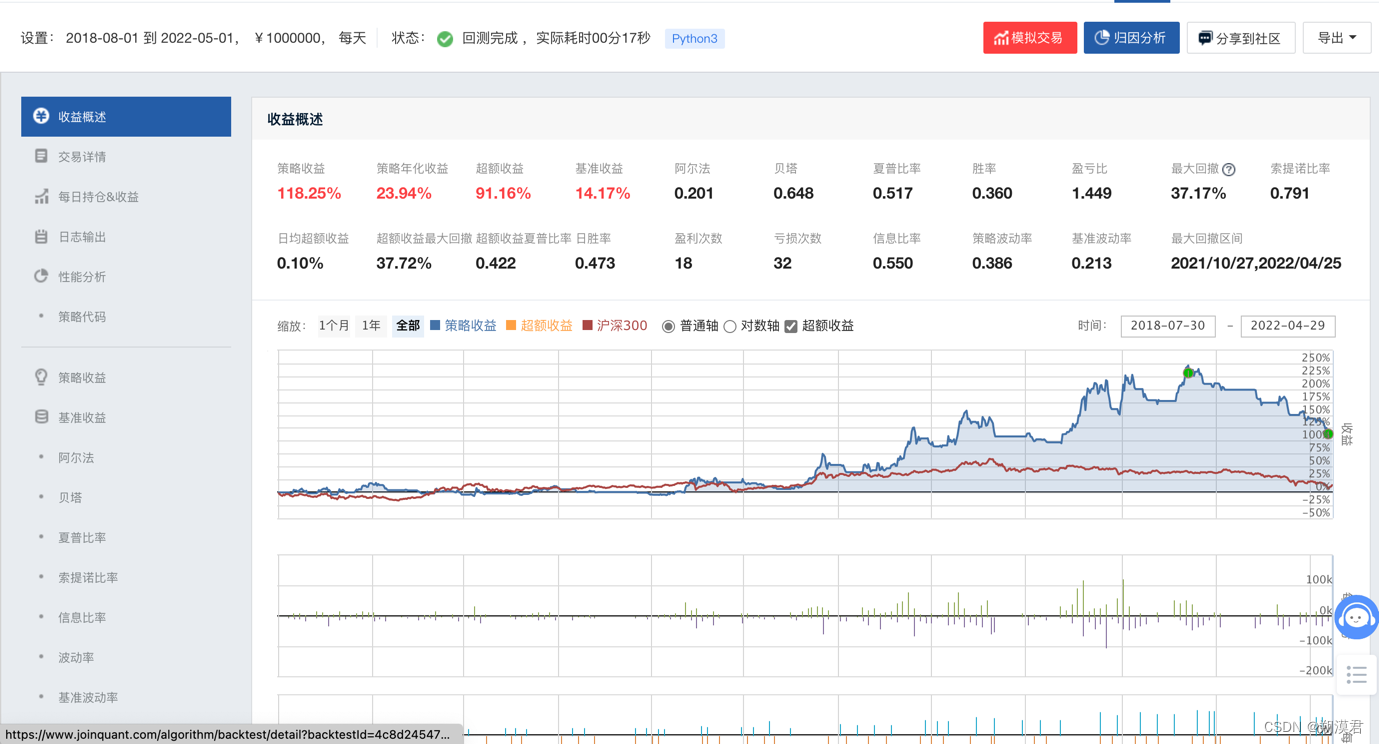
def after_market_close(context):log.info(str('函数运行时间(after_market_close):'+str(context.current_dt.time())))#得到当天所有成交记录trades = get_trades()for _trade in trades.values():log.info('成交记录：'+str(_trade))log.info('一天结束')log.info('##############################################################')