Hi,大家好,我是半亩花海。本文主要源自《第二届全国技能大赛智能制造工程技术项目比赛试题(样题) 模块 E 工业大数据与人工智能应用》,基于给出的已知轴承状态的振动信号样本,对数据进行分析,建立轴承故障诊断模型,对未知状态的振动信号样本进行预测,判断该样本属于哪种状态。
目录
技术描述
任务说明
任务一
一、导入必要库
二、读取并处理训练数据
三、绘制比例分布饼图
任务二
一、导入必要库
二、数据预处理
2.1 数据切片和分层抽样
2.2 轴承振动信号检视-时域分析
2.3 频域功率谱的分布¶
三、模型构建与训练
3.1 循环神经网络模型 (RNN)
3.3.1 构建 RNN 模型
3.3.2 训练 RNN 模型
3.1.3 可视化训练结果 (RNN)
3.2 卷积神经网络模型 (CNN)
3.2.1 构建 CNN 模型
3.2.2 训练 CNN 模型
3.2.3 可视化训练结果 (CNN)
3.3 多层感知器模型 (MLP)
3.3.1 构建 MLP 模型
3.3.2 训练 MLP 模型
3.3.3 可视化训练结果 (MLP)
四、模型预测
4.1 数据预处理
4.2 模型预测和结果保存
五、结果分析
技术描述
轴承是当代机械设备中一种重要零部件。它的主要功能是支撑机械旋转体,降低其运动过程中的摩擦系数,并保证其回转精度。由于轴承的关键作用和广泛使用,其健康状况直接影响着所在设备运行的稳定性与安全性,因此轴承故障的早期诊断具有重要意义。
传统的轴承故障诊断方法包括听声音、手持设备点检和测温度等,但是这些方法的缺点是对人的经验与感觉强依赖,难以传承和标准化,且实时性和精确性较差,往往检测到故障时故障已经很严重了。为了克服这些传统轴承故障诊断方法的缺点,现在轴承故障诊断的研究领域主要聚焦在将振动分析和大数据、人工智能等技术相结合,采用机理+数据驱动的方法来提升轴承故障诊断的效果。
常见的轴承故障如下图所示:

本试题的任务是基于给出的已知轴承状态(包括健康状态和不同故障状态)的振动信号样本,对数据进行分析,建立轴承故障诊断模型,对未知状态的振动信号样本进行预测,判断该样本属于哪种状态。
所提供的数据中包含 4 种不同状态的轴承振动信号样本,包括健康状态和 3 种不同的故障状态。每个样本为一组连续采集的轴承振动信号,下表为轴承振动信号的基本信息。
| 采样率 | 50Hz |
| 轴承转速 | 13.33Hz |
| 每组振动信号长度 | 40960 |
每一组振动信号样本对应一个轴承状态标签,下表为 4 种不同轴承状态的标签和相应的说明。
| 标签 | 说明 |
| normal | 健康 |
| inner | 内圈故障 |
| outer | 外圈故障 |
| roller | 滚动体故障 |
数据分为样本数据、样本标签和测试数据,样本数据混合了4种状态的样本,样本标签是各样本对应的轴承状态,测试数据是未知状态待检测的样本。数据存储在工业大数据平台中(有需要训练集和测试集的朋友可以在评论区或者私信我)。
任务说明
任务一
从工业大数据平台中查询数据,分析各种状态类型轴承样本的数量,制作一张比例分布饼图,要求有图例和占比数字标签。
一、导入必要库
import pandas as pd
import matplotlib.pyplot as plt
import warningswarnings.filterwarnings("ignore") # 忽略警告信息
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置黑体样式
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号二、读取并处理训练数据
train_data = pd.read_csv('train.csv')
labels = train_data['label'] # 提取标签列
print(train_data)
# 统计各标签数量并转换为字典
count_dict = labels.value_counts().to_dict()
三、绘制比例分布饼图
# 提取标签和对应的数量用于饼图
labels = list(count_dict.keys())
sizes = list(count_dict.values())
colors = ['blue', 'green', 'red', 'yellow'] # 为每个扇形定义颜色# 制作比例分布饼图
fig, ax = plt.subplots(figsize=(6, 6)) # 创建一个大小为6x6的figure对象
ax.pie(sizes, labels=labels, colors=colors, autopct='%1.1f%%', startangle=90, textprops={'fontsize': 12}) # 在ax上绘制饼图
# ax = plt.gca() # 返回坐标轴
ax.legend(loc='upper right', bbox_to_anchor=(1.1, 1.1), fontsize=10) # 添加图例
ax.axis('equal') # 保持纵横比相等, 确保饼图呈圆形
plt.title('轴承状态类型比例分布', fontsize=15) # 设置饼图标题plt.show() # 显示饼图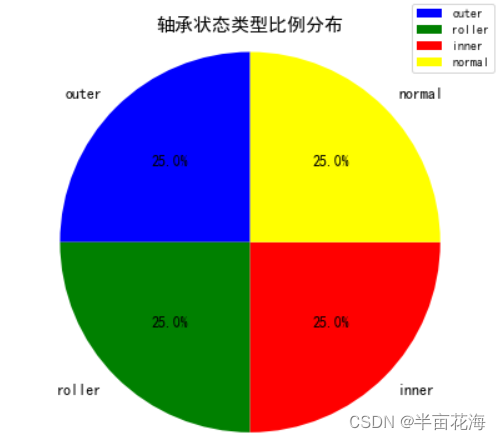
任务二
对样本数据进行分析,使用 Python 编程语言建立人工智能预测模型,通过模型判断测试数据对应的轴承状态,并保存在如下格式要求的文件中。
一、导入必要库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from tensorflow.keras.layers import Conv1D, SimpleRNN, MaxPooling1D, Flatten, Dense, Dropout
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import Sequential
from collections import defaultdict
import warningswarnings.filterwarnings("ignore") # 忽略警告信息
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置黑体样式
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号二、数据预处理
2.1 数据切片和分层抽样
# 读取训练数据
data = pd.read_csv('train.csv')# 将标签编码为数字
label_encoder = LabelEncoder()
data['label'] = label_encoder.fit_transform(data['label'])# 数据切片处理
X = []
y = []
for i in range(len(data)):row = data.iloc[i, 1:].values # 选择第i行的所有列(除第1列), 再将 DataFrame 行转换为 NumPy 数组row_reshaped = np.reshape(row[:len(row) // 512 * 512], (-1, 512)) # 将一维数组 row 切片并重新形状为一个二维数组, 每行包含512个元素X.extend(row_reshaped) # 将二维数据展开成一维数组y.extend(np.tile(data.iloc[i, 0], row_reshaped.shape[0])) # 在给定方向上重复数组: np.tile(要重复的数组, 重复的次数)
X = np.array(X)
y = np.array(y)# 对标签进行独热编码
y = to_categorical(y)# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) # 设置测试集占比25%, 随机种子422.2 轴承振动信号检视-时域分析
通过检视数据对信号进行时域分析,可以看到数据集中收集的是一个维度的振动信号,不同的标签对应的信号振幅应该有所不同。
f, ax = plt.subplots(2,2,figsize=(32,16))
state_list = ['normal', 'inner', 'outer', 'roller']
for i in range(2):for j in range(2):current_ax = ax[j][i]current_ax.title.set_text(state_list[2*j+i])# 提取数据current_data = list(data[data.label==2*j+i].iloc[0][1:513])# 绘制线图,并设置线宽、标记大小sns.lineplot(data=current_data, ax=current_ax, linewidth=2, markersize=10)# 调整横轴和纵轴刻度标签的字体大小current_ax.tick_params(axis='x', labelsize=16)current_ax.tick_params(axis='y', labelsize=16)# 调整标题的字体大小current_ax.title.set_fontsize(24)
plt.show() # 显示图形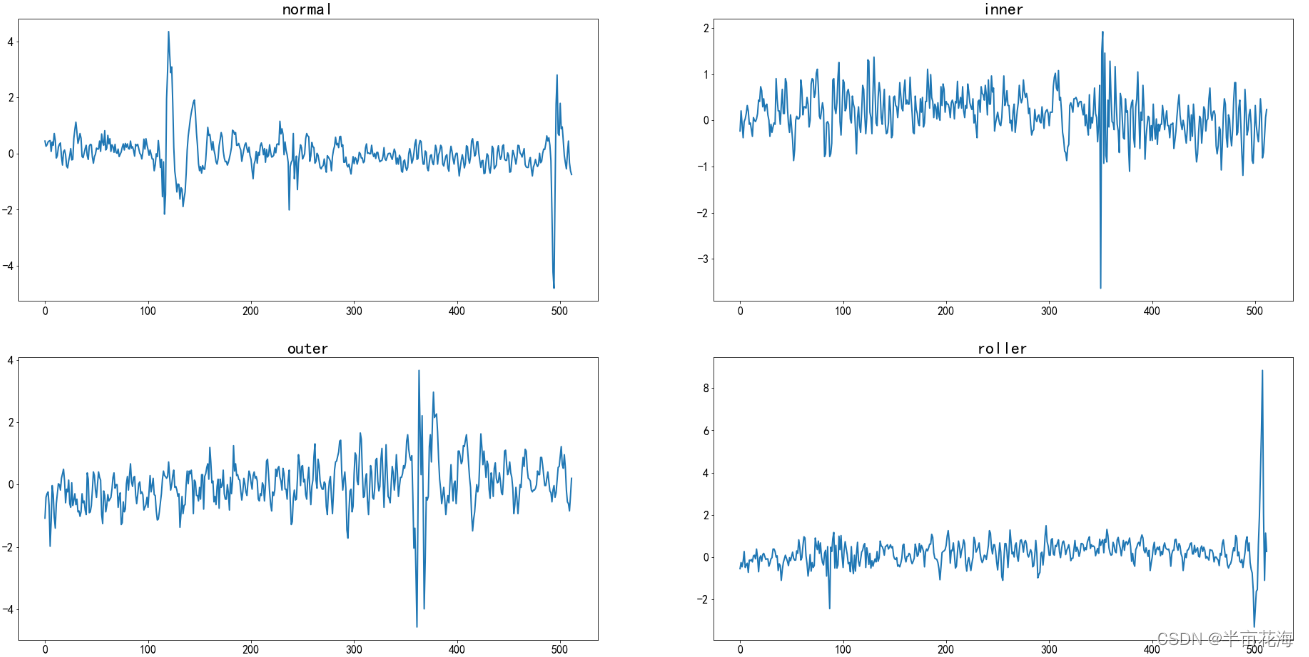
2.3 频域功率谱的分布¶
通过快速傅立叶变换对频域的功率谱做一个快速的可视化。
f, ax = plt.subplots(2,2,figsize=(32,16))
state_list = ['normal', 'inner', 'outer', 'roller']
for i in range(2):for j in range(2):current_ax = ax[j][i]current_ax.title.set_text(state_list[2*j+i])# 提取数据current_data = data[data.label==2*j+i].iloc[0][1:513]# 计算FFTfft = np.fft.fft(current_data)# 绘制线图,并设置线宽、标记大小sns.lineplot(data=(fft.real ** 2 - fft.imag ** 2), ax=current_ax, linewidth=2, color='red')# 调整横轴和纵轴刻度标签的字体大小current_ax.tick_params(axis='x', labelsize=16)current_ax.tick_params(axis='y', labelsize=16)# 调整标题的字体大小current_ax.title.set_fontsize(24)
plt.show() # 显示图形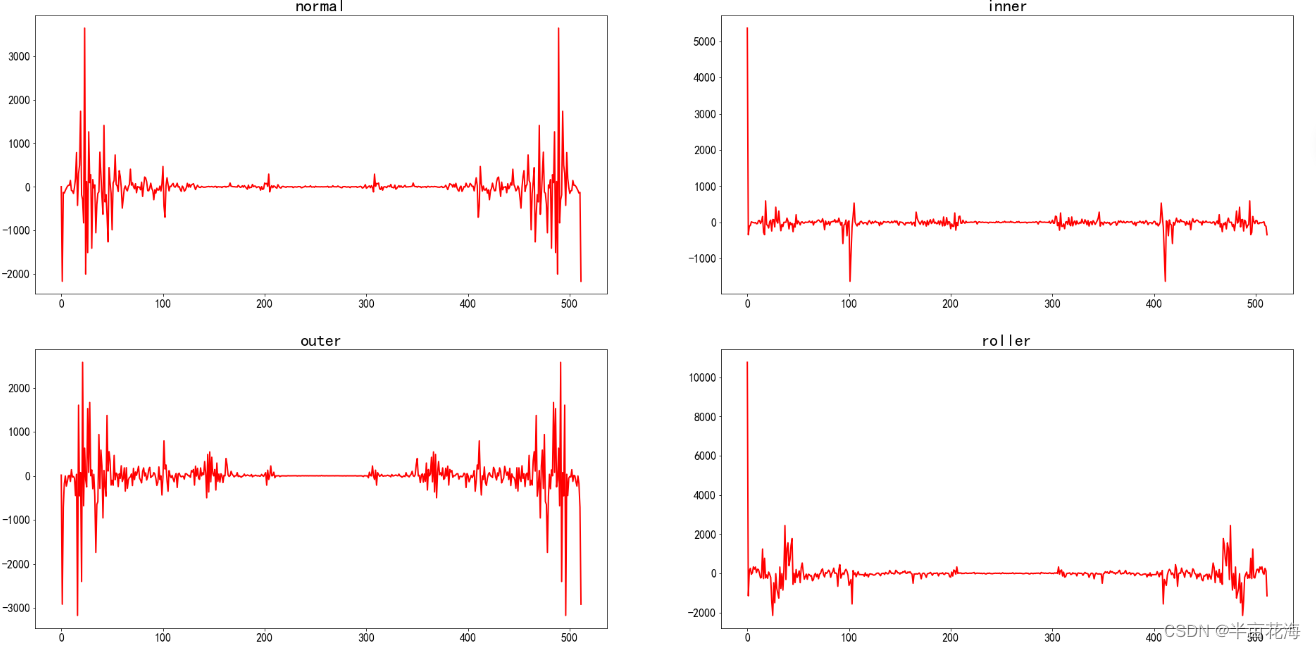
三、模型构建与训练
3.1 循环神经网络模型 (RNN)
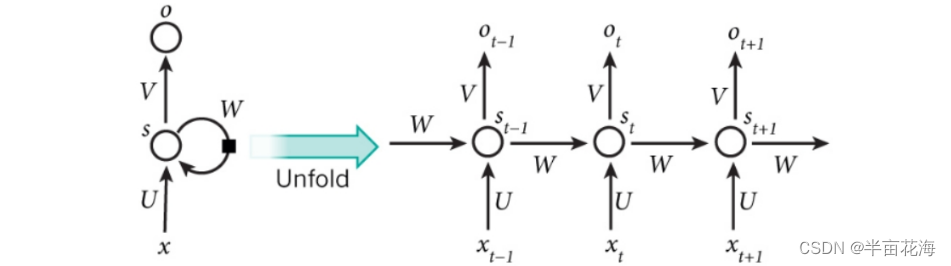
循环神经网络 (Recurrent Neural Network,RNN) 是一类具有短期记忆能力的神经网络。在循环神经网络中,神经元不但可以接受其它神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。RNN具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐藏层之间的节点不再无连接而是有连接的,并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。
RNN 网络中第 t 次的隐含层状态的计算公式为:
RNN 网络的特点:
- 这里的W,U,V在每个时刻都是相等的(权重共享)
- 隐藏状态可以理解为: S=f(现有的输入+过去记忆总结)
以下是一种典型的 RNN 结构中 Hidden Layer 层级展开图:
3.3.1 构建 RNN 模型
# 构建RNN模型
rnn_model = Sequential()
rnn_model.add(SimpleRNN(64, activation='relu', input_shape=(512, 1), return_sequences=True)) # SimpleRNN层, 64个单元, 激活函数ReLU, 输入形状(512, 1)
rnn_model.add(MaxPooling1D(pool_size=2)) # 一维最大池化层, 窗口大小为2
rnn_model.add(Flatten()) # 将多维数据展平为一维
rnn_model.add(Dense(128, activation='relu')) # 全连接层, 4个神经元, 激活函数为relu
rnn_model.add(Dropout(0.5)) # Dropout层, 丢弃率为0.5, 减少过拟合风险
rnn_model.add(Dense(4, activation='softmax')) # 全连接层, 4个神经元, 激活函数为softmax
rnn_model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 编译RNN模型 (交叉熵损失函数, Adam优化器,评估指标为准确率)3.3.2 训练 RNN 模型
# 训练RNN模型
history = rnn_model.fit(X_train.reshape(-1, 512, 1), y_train, epochs=30, batch_size=32,validation_data=(X_test.reshape(-1, 512, 1), y_test))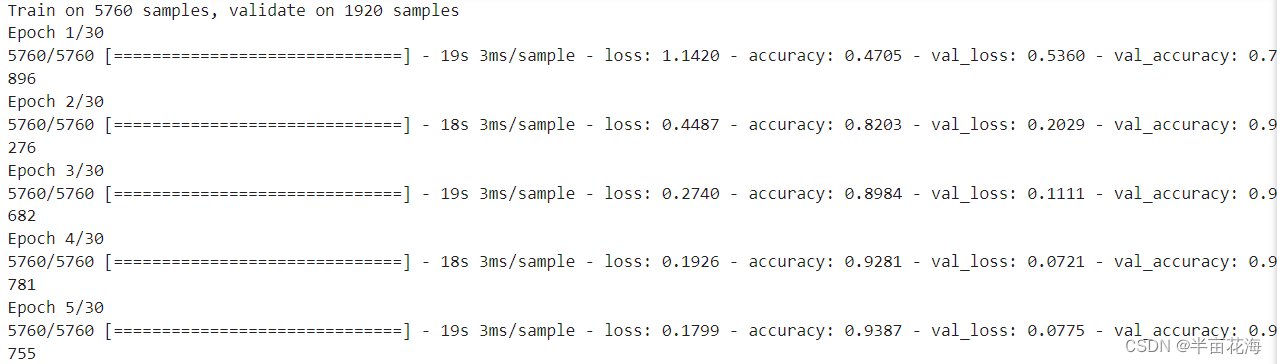
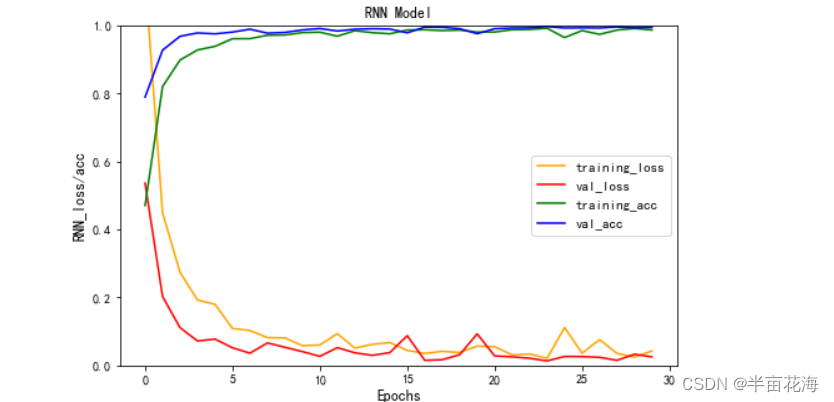
3.1.3 可视化训练结果 (RNN)
3.2 卷积神经网络模型 (CNN)
CNN 网络是一种带有卷积结构的前馈神经网络,卷积结构可以减少深层网络占用的内存量,其中三个关键操作——局部感受野、权值共享、池化层,有效的减少了网络的参数个数,缓解了模型的过拟合问题。
CNN 网络的主要结构如下:
| 输入层 | 卷积层 | 激活层 | 池化层 | 光栅化 | 全连接层 | 激活层 | 输出层 |
|---|---|---|---|---|---|---|---|
| 输入数据 | 使用卷积核特征提取和映射 | 非线性映射 | 下采样降维 | 展开像素, 联接全连接层 | 在尾部进行拟合, 减少特征损失 | 非线性映射 | 输出结果 |
CNN 网络的结构可视化如下:

3.2.1 构建 CNN 模型
# 构建CNN模型
Conv1D_model = Sequential()
Conv1D_model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(512, 1))) # 一维卷积层, 64个滤波器, 大小3, 激活函数relu, 输入形状(512, 1)
Conv1D_model.add(MaxPooling1D(pool_size=2)) # 一维最大池化层, 窗口大小为2
Conv1D_model.add(Flatten()) # 将多维数据展平为一维
Conv1D_model.add(Dense(128, activation='relu')) # 全连接层, 128个神经元, 激活函数relu
Conv1D_model.add(Dropout(0.5)) # Dropout层, 丢弃率为0.5, 减少过拟合风险
Conv1D_model.add(Dense(4, activation='softmax')) # 全连接层, 4个神经元, 激活函数为softmax
Conv1D_model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 编译CNN模型 (交叉熵损失函数, Adam优化器,评估指标为准确率)3.2.2 训练 CNN 模型
# 训练CNN模型
history = Conv1D_model.fit(X_train.reshape(-1, 512, 1), y_train, epochs=30, batch_size=32,validation_data=(X_test.reshape(-1, 512, 1), y_test))
3.2.3 可视化训练结果 (CNN)
# 绘制CNN模型的损失率和准确率曲线
plt.figure(figsize=(8, 5))
plt.plot(history.history['loss'], color='orange', label='training_loss') # 训练集损失率
plt.plot(history.history['val_loss'], color='red', label='val_loss') # 验证集损失率
plt.plot(history.history['accuracy'], color='green', label='training_acc') # 训练集准确率
plt.plot(history.history['val_accuracy'], color='blue', label='val_acc') # 验证集准确率
plt.title('CNN Model')
plt.legend(fontsize=11)
plt.xlabel('Epochs', fontsize=12)
plt.ylabel('CNN_loss/acc', fontsize=12)
plt.ylim(0, 1) # 设置纵坐标范围为0-1
plt.show()3.3 多层感知器模型 (MLP)
多层感知器也叫人工神经网络,除了输入层和输出层,它中间可以有多个隐层,最简单的 MLP 只含一个隐层,即三层的结构。MLP 神经网络属于前馈神经网络的一种。在网络训练过程中,需要通过反向传播算法计算梯度,将误差从输出层反向传播回输入层,用于更新网络参数。
MLP 模型的结构如下:

3.3.1 构建 MLP 模型
# 构建MLP模型
mlp_model = Sequential()
mlp_model.add(Dense(256, activation='relu', input_shape=(512,))) # 全连接层,256个神经元,激活函数ReLU,输入形状(512,)
mlp_model.add(Dropout(0.5)) # Dropout层,丢弃率为0.5,减少过拟合风险
mlp_model.add(Dense(128, activation='relu')) # 全连接层,128个神经元,激活函数ReLU
mlp_model.add(Dropout(0.5)) # Dropout层
mlp_model.add(Dense(64, activation='relu')) # 全连接层,64个神经元,激活函数ReLU
mlp_model.add(Dropout(0.5)) # Dropout层
mlp_model.add(Dense(4, activation='softmax')) # 输出层,4个神经元(对应4个类别),激活函数Softmax
mlp_model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 编译MLP模型 (交叉熵损失函数, Adam优化器,评估指标为准确率)3.3.2 训练 MLP 模型
# 训练MLP模型
history = mlp_model.fit(X_train.reshape(-1, 512), y_train, epochs=50, batch_size=32,validation_data=(X_test.reshape(-1, 512), y_test))
3.3.3 可视化训练结果 (MLP)
# 绘制MLP模型的损失率和准确率曲线
plt.figure(figsize=(8, 5))
plt.plot(history.history['loss'], color='orange', label='training_loss') # 训练集损失率
plt.plot(history.history['val_loss'], color='red', label='val_loss') # 验证集损失率
plt.plot(history.history['accuracy'], color='green', label='training_acc') # 训练集准确率
plt.plot(history.history['val_accuracy'], color='blue', label='val_acc') # 验证集准确率
plt.title('MLP Model')
plt.legend(fontsize=11)
plt.xlabel('Epochs', fontsize=12)
plt.ylabel('MLP_loss/acc', fontsize=12)
plt.ylim(0, 1) # 设置纵坐标范围为0-1
plt.show()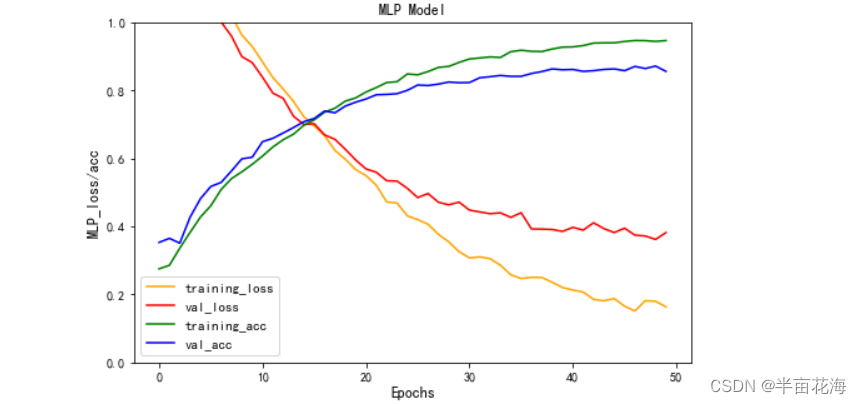
四、模型预测
4.1 数据预处理
# 读取测试数据
test_data = pd.read_csv('test_data.csv')# 测试集数据预处理
X_test = []
sample_names = []
for i in range(len(test_data)):row = test_data.iloc[i, 1:].valuesrow_reshaped = np.reshape(row[:len(row) // 512 * 512], (-1, 512))X_test.extend(row_reshaped)sample_names.extend([f"sample {i}"] * row_reshaped.shape[0])
X_test = np.array(X_test)4.2 模型预测和结果保存
# 定义一个模型预测并结果保存的函数
def predict_and_save(model, X_test, output_filename):# 使用模型进行预测predictions = model.predict(X_test)# 获取预测结果中概率最高的类别predicted_labels = np.argmax(predictions, axis=1)# 定义类别映射关系,将数值标签映射到相应的类别labels_mapping = {0: 'normal', 1: 'inner', 2: 'outer', 3: 'roller'}predicted_classes = [labels_mapping[label] for label in predicted_labels]# 创建包含样本名和预测类别的 DataFramefinal_predictions = pd.DataFrame({'name': sample_names, 'type': predicted_classes})# 对每个样本取众数(出现频率最高的类别)final_predictions = final_predictions.groupby('name')['type'].agg(lambda x: x.mode().iat[0]).reset_index()# 从样本名中提取样本编号并对 DataFrame 进行排序final_predictions['name'] = final_predictions['name'].apply(lambda x: int(x.split(' ')[-1]))final_predictions = final_predictions.sort_values(by='name')# 格式化样本名并将结果保存到 csv 文件中(不保存行索引)final_predictions['name'] = final_predictions['name'].apply(lambda x: f"sample {x}")final_predictions.to_csv(output_filename, index=False)# 调用 predict_and_save 函数对模型进行预测并保存结果
predict_and_save(rnn_model, X_test.reshape(-1, 512, 1), 'test_rnn.csv')
predict_and_save(Conv1D_model, X_test.reshape(-1, 512, 1), 'test_cnn.csv')
predict_and_save(mlp_model, X_test.reshape(-1, 512), 'test_mlp.csv')
五、结果分析
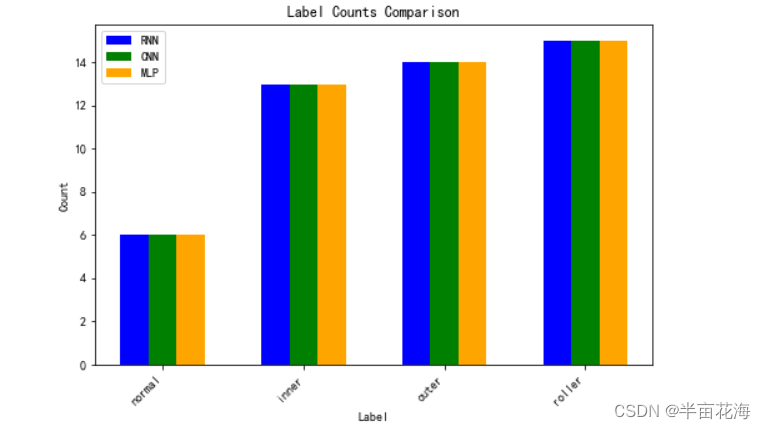
通过读取每个模型的测试结果文件,输出各个标签的数量,并且以直方图来可视化三个模型的标签数量。结果显示 RNN、CNN 和 MLP 模型预测的结果相同。
# 读取各个模型的测试结果文件
rnn_result = pd.read_csv('test_rnn.csv')
cnn_result = pd.read_csv('test_cnn.csv')
mlp_result = pd.read_csv('test_mlp.csv')# 输出各个标签的数量
def output_label_counts(result, model_name):label_counts = result['type'].value_counts()print(f"\n{model_name} Label Counts:")for label in ['normal', 'inner', 'outer', 'roller']:count = label_counts.get(label, 0)print(f"{label}: {count}")output_label_counts(rnn_result, 'RNN')
output_label_counts(cnn_result, 'CNN')
output_label_counts(mlp_result, 'MLP')# 可视化各个模型的标签数量(直方图)
plt.figure(figsize=(8, 5))
def plot_label_counts(result, model_name, index, color):label_counts = result['type'].value_counts()counts_in_order = [label_counts.get(label, 0) for label in ['normal', 'inner', 'outer', 'roller']]plt.bar(np.arange(len(counts_in_order)) + 0.2 * index, counts_in_order, width=0.2, label=model_name, color=color)# 绘制三个模型的直方图并指定颜色
plot_label_counts(rnn_result, 'RNN', 0, 'blue')
plot_label_counts(cnn_result, 'CNN', 1, 'green')
plot_label_counts(mlp_result, 'MLP', 2, 'orange')# 添加图例、标题和标签
plt.legend()
plt.title('Label Counts Comparison')
plt.xlabel('Label')
plt.ylabel('Count')
plt.xticks(np.arange(4) + 0.2, ['normal', 'inner', 'outer', 'roller'], rotation=45, ha='right')
plt.show()RNN Label Counts:
normal: 6
inner: 13
outer: 14
roller: 15
CNN Label Counts:
normal: 6
inner: 13
outer: 14
roller: 15
MLP Label Counts:
normal: 6
inner: 13
outer: 14
roller: 15





 —— (DBMS存储空间管理)】)







)


)

hadoop之hive的搭建1)
