今天做两个有点难度的题。
1、295. 数据流的中位数
手写堆实现:
加入元素:
如何维护一个中位数?我们考虑一下堆的特点,大顶堆堆顶是一个最大值,小顶堆堆顶是一个最小值,那么,如果我们可以把数据流的数据按顺序地平均地存放在两个堆中,一个大顶堆,一个小顶堆,那么大顶堆和小顶堆的堆顶不就是中位数吗?
就像下图这样,我们依次加入数据流,最后需要形成这样的堆。

还需要考虑一个问题,我们怎样加入元素?肯定是加一下大顶堆,再加一下小顶堆,这样依次加入元素,但是能直接就加吗?
不可以的,因为我们的大顶堆需要存储小的那部分元素,小顶堆需要存储大的那部分元素。
这里需要一个巧妙地操作,比如我们每次要往大顶堆添加元素,先把这个元素加到小顶堆,然后把小顶堆的堆顶加到大顶堆中。
比如,此时来了个100,两个堆size相同,我们想加到大顶堆中

但是100很大,所以我们先加入小顶堆,然后小顶堆堆顶移到大顶堆
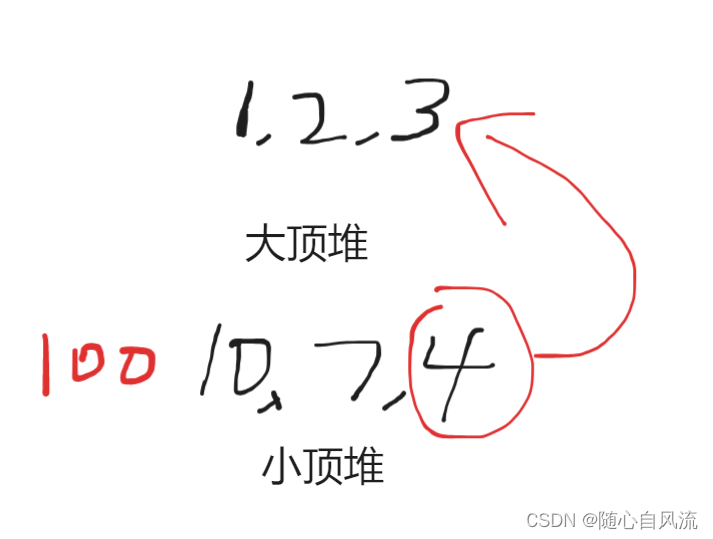
这样就实现了元素加入大顶堆并且大小有序。

加入代码如下:h1大顶堆,h2小顶堆。
if(h1.size == h2.size){h2.offer(num);h1.offer(h2.poll());}else{h1.offer(num);h2.offer(h1.poll());}返回答案
如果元素相同,返回堆头之和除以2;如果不同,那肯定是大顶堆h1多一个元素,直接返回就行。注意结果是double类型。
if(h1.size == h2.size){return (h1.peek() + h2.peek())/2.0;}return 1.0*h1.peek();这里我手写一下堆,复习一下堆的基本写法。
h1 = new Heap(10, true);
h2 = new Heap(10, false);
第二个参数是true代表大顶堆,是false代表小顶堆,我将大小顶堆代码合并了。
class MedianFinder {Heap h1 = null;Heap h2 = null;public MedianFinder() {h1 = new Heap(10, true);h2 = new Heap(10, false);}public void addNum(int num) {if(h1.size == h2.size){h2.offer(num);h1.offer(h2.poll());}else{h1.offer(num);h2.offer(h1.poll());}}public double findMedian() {if(h1.size == h2.size){return (h1.peek() + h2.peek())/2.0;}return 1.0*h1.peek();}
}
class Heap{private int[] array;int size;Boolean m;public Heap(int capacity, Boolean m) {this.array = new int[capacity];this.m = m;}public int peek(){return size==0 ? -999 : array[0];}public void offer(int offered){if(size == array.length) {resize();}up(offered);size++;}private void resize() {int capacity = size + (size>>1);int[] newArr = new int[capacity];System.arraycopy(array, 0, newArr, 0, size);array = newArr;}private void up(int offered) {int child = size;while(child > 0){int parent = (child - 1) / 2;if(m ? offered > array[parent] : offered < array[parent]){array[child] = array[parent];}else {break;}child = parent;}array[child] = offered;}public int poll(){int top = array[0];swap(0, size-1);size--;down(0);return top;}private void down(int i) {int lc = 2*i+1;int rc = lc+1;int now = i;if(lc < size && (m ? array[lc] > array[now] : array[lc] < array[now])){now = lc;}if(rc < size && (m ? array[rc] > array[now] : array[rc] < array[now])){now = rc;}if(now != i){swap(now, i);down(now);}}private void swap(int top, int bottom) {int t = array[top];array[top] = array[bottom];array[bottom] = t;}
}
利用优先队列:
优先队列底层就是堆嘛,所以直接用java提供的优先队列也行。( •̀ ω •́ )y
class MedianFinder {PriorityQueue<Integer> q1;PriorityQueue<Integer> q2;public MedianFinder() {q1 = new PriorityQueue<>((o1, o2)->o2-o1);q2 = new PriorityQueue<>();}public void addNum(int num) {if(q1.size() == q2.size()){q2.offer(num);q1.offer(q2.poll());}else{q1.offer(num);q2.offer(q1.poll());}}public double findMedian() {return (q1.size()==q2.size() ? 1.0*(q1.peek()+q2.peek())/2 :1.0*q1.peek());}
}2、239. 滑动窗口最大值
第一想法,直接来个优先队列,但是想想不对,因为优先队列会将窗口中的数据排序,排完序之后窗口继续移动,那我就无法知道应该pop掉哪个元素了。
我们需要一个数据结构,这个数据结构和队列很像,它能push加入队尾,pop删除队头,getMaxValue获取最大值。但是并没有这种现成的数据结构。
实现上面需求的数据结构叫做单调队列。
单调队列中存着窗口中的元素,队列头就是当前窗口最大值,为什么能是最大值呢?因为这个队列并不是存储所有的元素,而是有选择的存,单调队列每次新加元素时,都会比较与队尾的值,如果队尾小,就一直pop,直到能添加进去,所以,如果此时新加的元素是最大值,那么它会pop掉所有队元素,成为队头。
所以,想要在单调队列中存活,需要满足两个条件:
- 在窗口的范围内
- 没有被新来的元素干掉,也就是不比新来的元素小
java中,我使用LinkedList,LinkedList实现了双端队列接口,用双端队列来模拟单调队列。
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {LinkedList<Integer> list = new LinkedList<>();//nums.length-k+1int len = nums.length;int[] ans = new int[len-k+1];int cnt = 0;for(int i = 0; i < len; i++){//弹出过时的while(!list.isEmpty() && list.peek() < i-k+1){list.poll();}//弹出末尾不够大的while(!list.isEmpty() && nums[list.peekLast()] < nums[i]){list.pollLast();}list.offer(i);if(i >= k-1){ans[cnt++] = nums[list.peek()];}}return ans;}
})








——登录拦截器)
QT Quick Controls2新颖界面开发)


,无需服务器,使用github托管)





