1094. 拼车

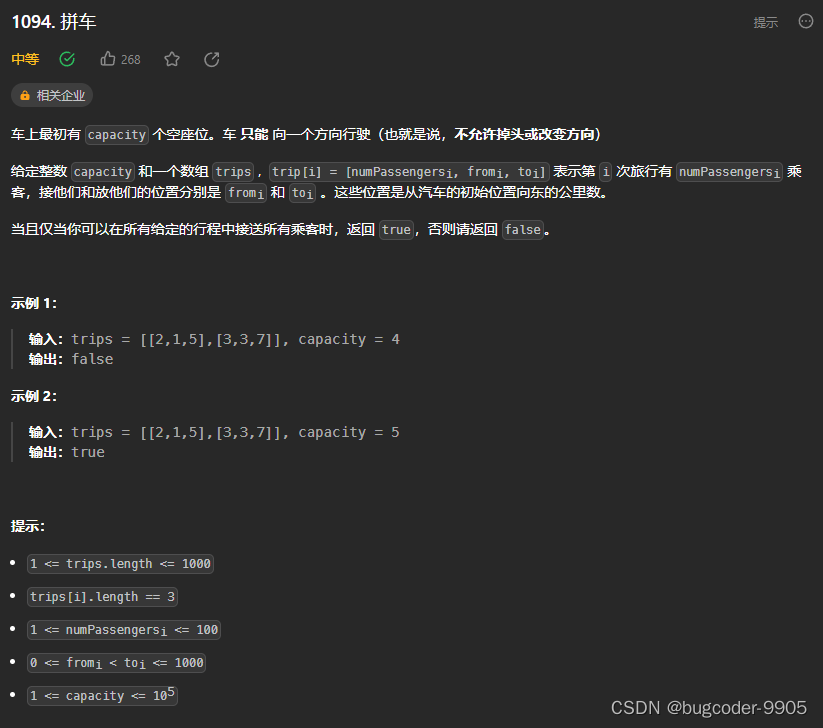
在这里插入图片描述

class Solution {public boolean carPooling(int[][] trips, int capacity) {int[] diff = new int[1001]; // 记录每个站点改变的人数，比如增加几个人，减少几个人for(int[] trip : trips){int cnt = trip[0];int from = trip[1];int to = trip[2];diff[from] += cnt;diff[to] -= cnt;}int num = 0; // 记录每个站点车上的人数for(int i = 0; i < 1001; i++){num += diff[i];if(num > capacity){return false;}}return true;}
}

1109. 航班预定统计

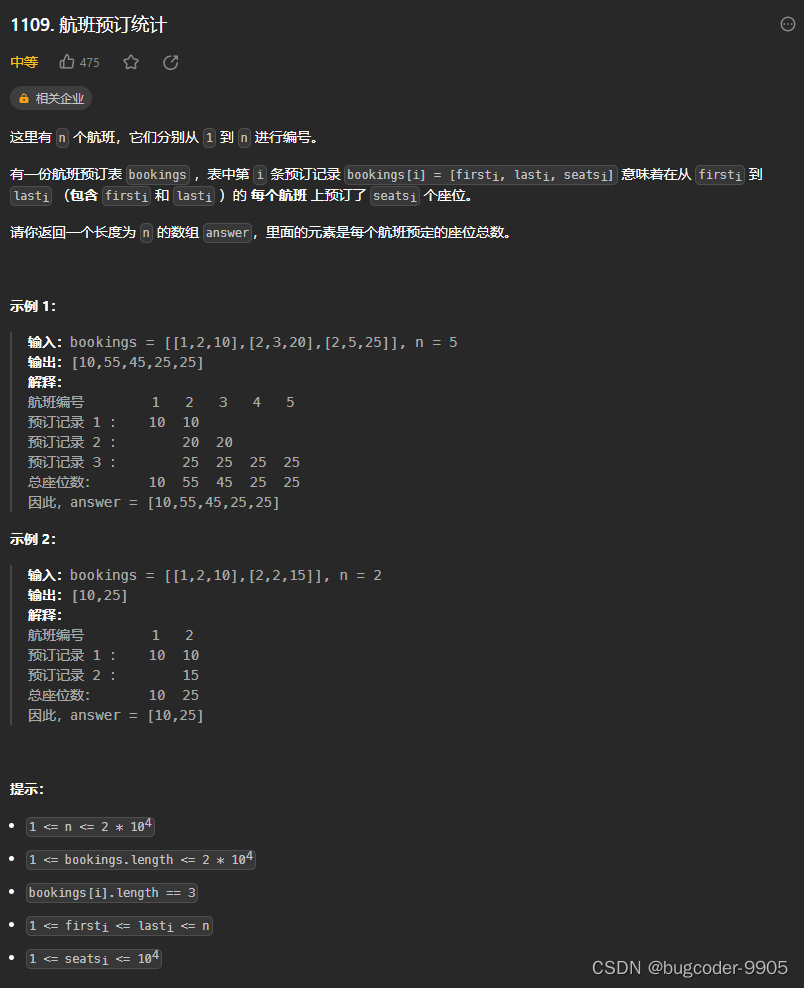
在这里插入图片描述

原数组后一位元素 - 前一位元素，得到的就是差分数组

通过差分数组求前缀和，可以得到原数组。对原数组区间[l, r]增加inc，相当于对差分数组的diff[l] += inc，diff[r + 1] -= inc

class Solution {public int[] corpFlightBookings(int[][] bookings, int n) {int[] diff = new int[n];int m = bookings.length;for(int i = 0; i < m; i++){int l = bookings[i][0];int r = bookings[i][1];int cnt = bookings[i][2];diff[l - 1] += cnt;if(r < n) diff[r] -= cnt;}for(int i = 1; i < n; i++){diff[i] += diff[i - 1];}return diff;}
}

303. 区域和检索 - 数组不可变

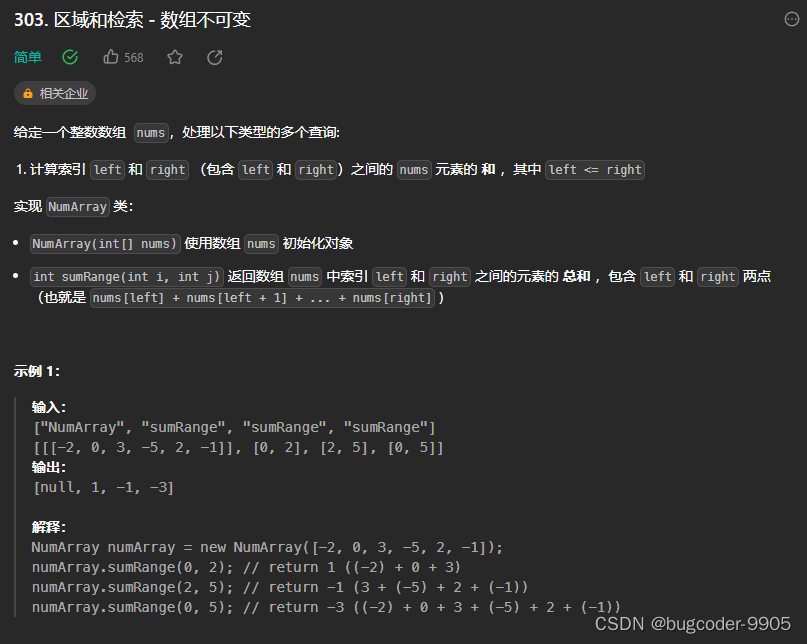
在这里插入图片描述

我们对原数组的[l, r]区间求和，可以转换为前缀和数组的差：pre[r] - pre[l - 1]

对前缀和求差分数组，可以得到原数组
对差分数组求前缀和，也可以得到原数组

class NumArray {int n;int[] pre;public NumArray(int[] nums) {n = nums.length;pre = new int[n];pre[0] = nums[0];for(int i = 1; i < n; i++){pre[i] = pre[i - 1] + nums[i];}}public int sumRange(int l, int r) {if(l == 0) return pre[r];return pre[r] - pre[l - 1];}
}

560. 和为K的子数组

在这里插入图片描述

class Solution {public int subarraySum(int[] nums, int k) {// 也就是前缀和数组两数之差为kint n = nums.length;int[] pre = new int[n];pre[0] = nums[0];for(int i = 1; i < n; i++){pre[i] = pre[i - 1] + nums[i];}int ans = 0;// presum, cntHashMap<Integer, Integer> map = new HashMap<>();map.put(0, 1);   // 表示pre[i]就是k，即[0,i]和为kfor(int i = 0; i < n; i++){if(map.containsKey(pre[i] - k)){ans += map.get(pre[i] - k);}map.put(pre[i], map.getOrDefault(pre[i], 0) + 1);}return ans;}
}

523. 连续的子数组的和

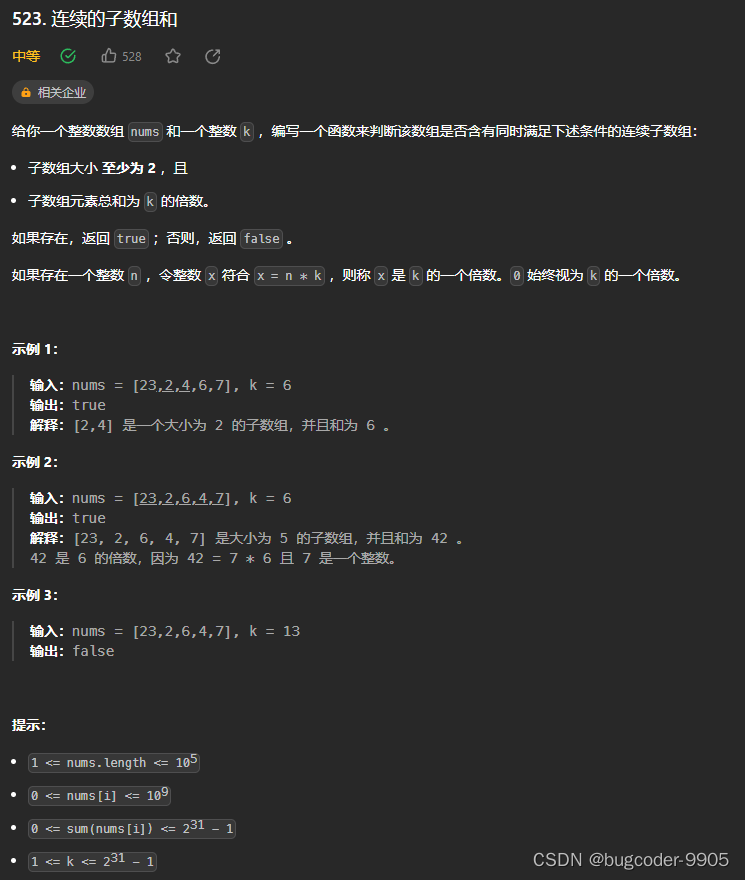
在这里插入图片描述
若区间和为k的整数倍，说明前缀和数组两个元素的差应该是k的整数倍，也即每个元素%k后，余数相同。余数相同，则表示两数之差是k的整数倍

class Solution {public boolean checkSubarraySum(int[] nums, int k) {int n = nums.length;int[] pre = new int[n];pre[0] = nums[0];for(int i = 1; i < n; i++){pre[i] = pre[i - 1] + nums[i];}HashMap<Integer, Integer> map = new HashMap<>();map.put(0, -2); // 如果前缀和数组 某个数 % k 的余数就是0，说明[0, i]区间的和就是k的整数倍，下标设置为-2for(int i = 0; i < n; i++){if(map.containsKey(pre[i] % k)){if(i > 0 && i - map.get(pre[i] % k) >= 2){// 同余的同时，还需要满足i > 0，因为i == 0时数组长度是1return true;}}else{// 余数已经出现过了，就不再更新了map.put(pre[i] % k, i);}}return false;}
}