PyTorch][chapter 13[李宏毅深度学习][Semi-supervised Linear Methods-2]

前言：

接上篇CSDN

这里面重点讲下面4个方面

PCA-Another Point of view（SVD）
PCA 和 AutoEncoder 的关系
PCA 的缺点
PCA Python 例子

一 PCA-Another Point of view

以手写数字7的图像为例，它由不同的笔画结构组成,分别为

$u^1,u^2,..u^k$

则手写数字7可以表示为

$x\approx c_1u^1+c_2u^2+..c_ku^l+\bar{x}$

上图 $c_1=1,c_2=1,c_3=c_4=c_5=0$

$x-\bar{x}\approx \hat{x}=c_1u^1+c_2u^2+...c_ku^k$

1.1 损失函数

我们要找到一组向量 $u^1,u^2,..u^k$ 使得

$L=||( x-\bar{x} )- \hat{x}||_2$ 最小(公式1.1）

有论文证明过，这个最优解就是SVD 奇异分解结果

1.2 PCA 降维原理回顾

$z=Wx$

$\begin{bmatrix} z_1\\ z_2 \\ ... \\ z_k \end{bmatrix}=\begin{bmatrix} w_1^T\\ w_2^T \\ ... \\ w_k^T \end{bmatrix}x$

这个特征向量 $W_1,W_2..W_k$ 是 $S=(x-\bar{x})(x-\bar{x})^T$ 的特征向量
这个解可以使得损失函数L公式1.1 最小，在Bitshop chapter12.1.2 里面有证明

1.3 SVD 奇异分解

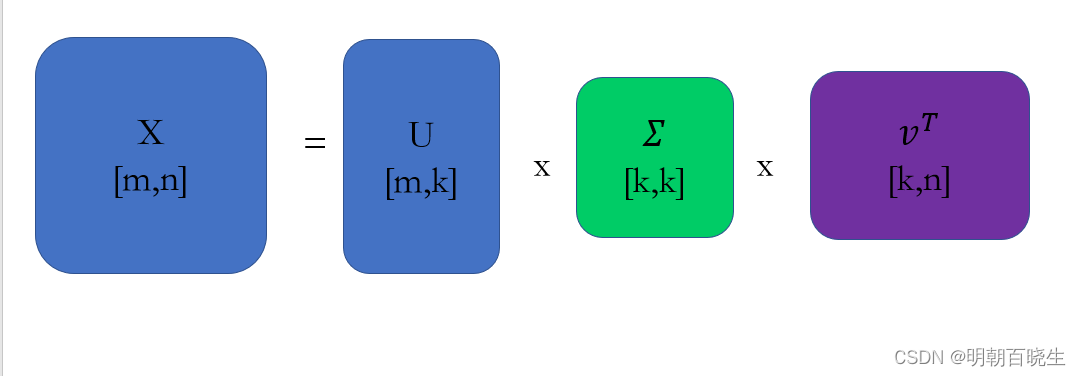
任意矩阵X（m,n），都可以将其分解为如下的形式

$X=U\sum V^T$

U：酉矩阵，亦称么正矩阵（单位正交），由对称矩阵 $XX^T$ 的特征向量组成。（与W的奇异值的顺序一致）
$\sum$ ：对角矩阵，由对称矩阵 $XX^T$ 或 $X^TX$ 的特征值的开平方组成，称为奇异值（从大到小排列，U和 $V^T$ 对应的特征向量亦如此）
$V^T$ ：酉矩阵，亦称么正矩阵（单位正交），由对称矩阵 $X^TX$ 的特征向量组成。（与 $\sum$ 的奇异值的顺序一致）

1.4 PCA 和 SVD 关系

假设我们有m笔数据 $x^1,x^2,..x^m$

第1笔数据 $x^1-\bar{x}=u^1c_1^1+u^2c_2^1+..$

第2笔数据 $x^2-\bar{x}=u^1c_1^2+u^2c_2^2+..$

第3笔数据 $x^3-\bar{x}=u^1c_1^3+u^2c_2^3+..$

我们发现可以用SVD 求上面的解

其中U 就是 $(x-\bar{x})(x-\bar{x})^T$ 的特征向量，跟PCA 中的协方差是一个东西

asso = np.cov(x, rowvar=False)

二 PCA 和 AutoEncoder 的关系

PCA 通过求解 $x\sim R^{n,1}$ 的协方差矩阵的特征值，特征向量得到投影矩阵 $W\sim R^{k,n}$

降维得到 :

投影： $z=Wx$

还原： $x=W^Tz$ 因为W 每一行之间都是正交基（不同特征值之间正交）

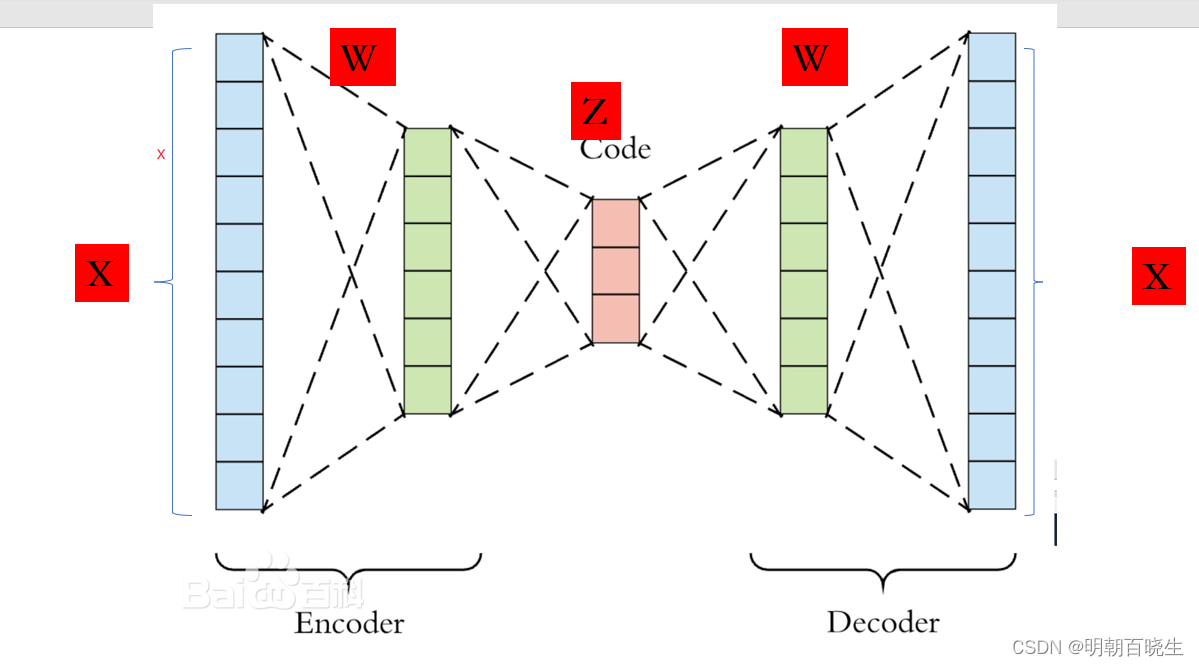
在神经网络里面可以通过AutoEncoder 来实现

编码器Encoder：

$z=W_1x$ ，模仿投影到低维空间功能

解码器Decoder：

$\hat{x}=W_2z$ 模仿还原到高维空间的功能

问题：

针对重构误差
$\hat{x}=x-\bar{x}=\sum_k c_kw_k$

如果可以线性重构：

三 PCA 的缺点

3.1 主成分选择：

选择较少的主成分可以实现较高的压缩率，但可能会丢失一些重要信息。而选择较多的主成分可能会保留过多的冗余信息。因此，在选择主成分的数量时需要权衡

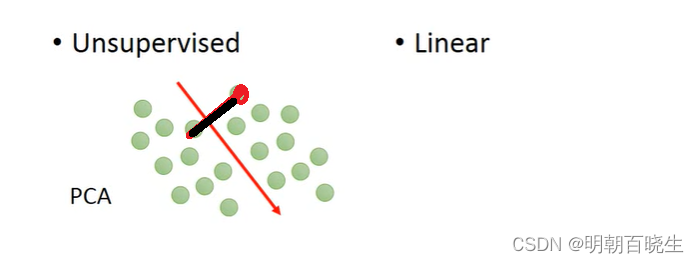
比如上图，红色点核绿色点两类。降低到一维上（红线）这个时候不同类别的特征信息就丢失了

在低维度空间无法区分.

3.2 非线性问题：

PCA是一种线性降维方法，它假设数据是线性可分的。对于非线性问题，PCA可能无法捕捉到数据的复杂结构。针对非线性问题，可以使用核PCA或其他非线性降维方法。

3,3数据预处理：

PCA对数据的预处理要求较高。标准化是必要的，因为PCA是基于特征之间的协方差矩阵进行计算的。如果数据不经过合适的预处理，可能会导致结果不准确或不可靠。

3.4 特征向量取多少个

原数据维度为d,降维维度为k. 这个k 到底怎么取

可以设置一个重构阀例t =95%

需要K 满足下面条件即可：

从大到小取特征值的绝对值

$a=\sum_{i=1}^K \lambda_i$

$b=\sum_{i=1}^d \lambda_i$

$\frac{a}{b}\geq t$

四 PCA Python 例子

# -*- coding: utf-8 -*-
"""
Created on Fri Feb  2 11:29:42 2024@author: chengxf2
"""import numpy as npdef calcCov(isAPI=True, data=None):'''isAPI : 是否通过直接调用API 方式data:   默认是每一行代表一个样本，每一列是一个维度，因为要降维所以做转置'''X = data.T#  m,n = np.shape(X)if True == isAPI:cov = np.cov(X,bias=False)print("\n api cov \n ",cov)else:#计算均值u = np.mean(X,axis=1,keepdims=True)m,n = np.shape(X)print(n)bias= X-u#print("\n 每一行是一个维度\n",X)#print("\n 均值 ",u)#print("\n x-u",a)cov = np.matmul(bias,bias.T)/(n-1)print("\n cov",cov)return covprint("\n API 协方差",cov)class PCA():def __init__(self, k):self.k = 0def obtain_features(self, eigVals, eigVecs,proportion):total = sum(abs(eigVals))print("\n 特征值 \n ",eigVals)m,n = np.shape(eigVecs)W= []eig_pairs = [(np.abs(eigVals[i]), list(eigVecs[:,i])) for i in range(n)]# 从大到小排序eig_pairs.sort(reverse=True)# select the top k eig_vecnumerator = 0k=0for paris in eig_pairs:val, eig = parisnumerator =numerator+valratio = numerator/totalk=k+1W.append(eig)if ratio>proportion:#每一行为一个特征向量#print("\n 特征向量",W)print("\n 特征向量维度",np.shape(W))breakW = np.array(W)return W.Tdef fit(self,data):#计算协方差矩阵cov = calcCov(True, data)#取总体能力的百分比proportion =0.8eigVals, eigVecs = np.linalg.eig(cov)self.W = self.obtain_features(eigVals, eigVecs, proportion)return self.Wdef reduction(self,data,W):#数据进行降维#data :m,n 每列为对应的属性#W: [n,k] 降到K维A = np.matmul(data, W)print(A.shape)return Adef main():data = np.random.rand(10,8)net = PCA(3)W= net.fit(data)net.reduction(data, W)if __name__ == "__main__":main()

参考：

13: Unsupervised Learning - Linear Methods_哔哩哔哩_bilibili

CSDN

基于PyTorch的PCA简单实现 - 知乎

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/662616.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！