本文主要参考:
【建议收藏】同济七版《高等数学》精讲视频 | 期末考试 | 考研零基础 | 高数小白_哔哩哔哩_bilibili
4.1.1.1 定积分引例_哔哩哔哩_bilibili
仅供本人学习使用。
积分是一个在多个领域都广泛使用的概念,特别是在数学和物理学中。
以下是积分的一些关键点:
积分作为微积分学与数学分析的核心概念之一,可以分为定积分和不定积分两种类型。
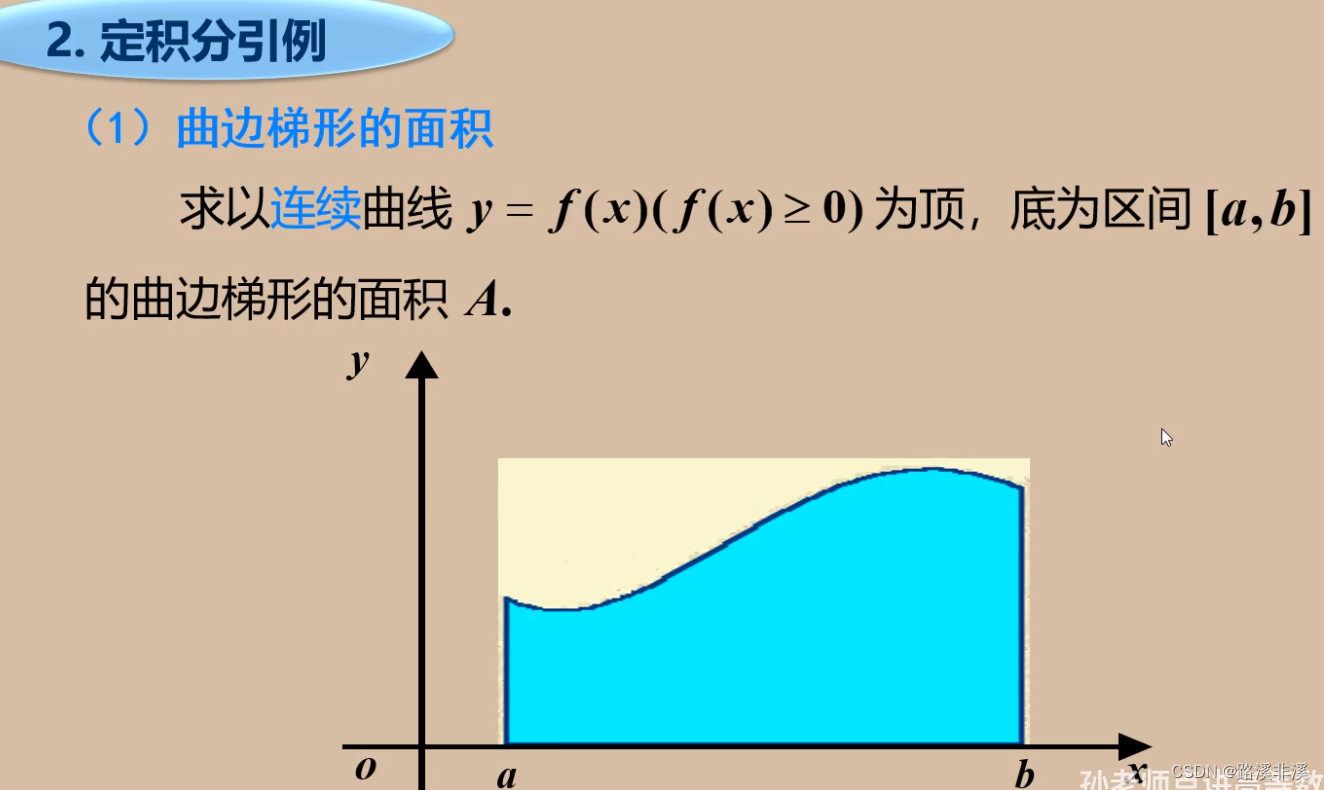
定积分可以被形象地理解为在坐标平面上,由曲线、直线以及坐标轴围成的曲边梯形的面积值,这是一个确定的实数值。积分的一个重要数学定义是由波恩哈德·黎曼给出的,他使用了极限的概念,将曲边梯形视为一系列矩形组合的极限。
积分具有特殊性质,如可加性和线性性,使得它可以用于计算曲边多边形和三角形的面积。此外,积分也是微分的逆运算,这意味着如果知道函数的导函数,可以通过积分反推原函数。
不定积分
不定积分是啥?
不定积分是微分的逆运算,求某一个函数的原函数的运算。
所以说,不定积分只是用来求原函数的一种方法,可以根据导函数求得原函数。
原函数的定义
一个函数求导得到导函数,那么原来的函数就是这个导函数对应的原函数,很好理解。
连续函数一定有原函数。
不定积分
这里带有任意项是说带有任意的常数项,因为常数求导后是0,所以知道一个导数再求原函数,原来的函数可能有一个常数项,这个常数项可能是任意常数C,所以才说是带有任意项的原函数。
不定积分和原函数的关系
这里稍微有些绕,绕来绕去,变换来变换去,但本质都是一样的。
不定积分从形式上来看,积的就是微分。
得到的就是带有任意常数项的原函数。
不定积分的性质
基本积分公式
积分就是求导的逆运算,或者说是微分的逆运算,但本质上就是找到导函数的原函数。
举个例子
参考的是上面的第(2)个积分公式。
有候直接积分不好积,可以尝试先化简或者转化成其他的等价形式,然后再积分。
比如:
换元积分法
换元积分法(Integration By Substitution)是求积分的一种方法,主要通过引进中间变量作变量替换,使得原式变得简易,从而来求较复杂的不定积分。
第一类换元法
就是找到一个整体,然后看能不能转化成对整体进行积分。
举个例子:
再举个例子:
第二类换元法
对比第一类换元法,第一类换元法是在原来的式子里凑一个整体;第二类换元法是直接将x用一个函数替换掉。
那选什么函数来替换x呢?
一般是根据经验来尝试,有几类总结如下:
第二类积分法求出的结果是关于替换函数的变量的函数,所以还要还原回去。
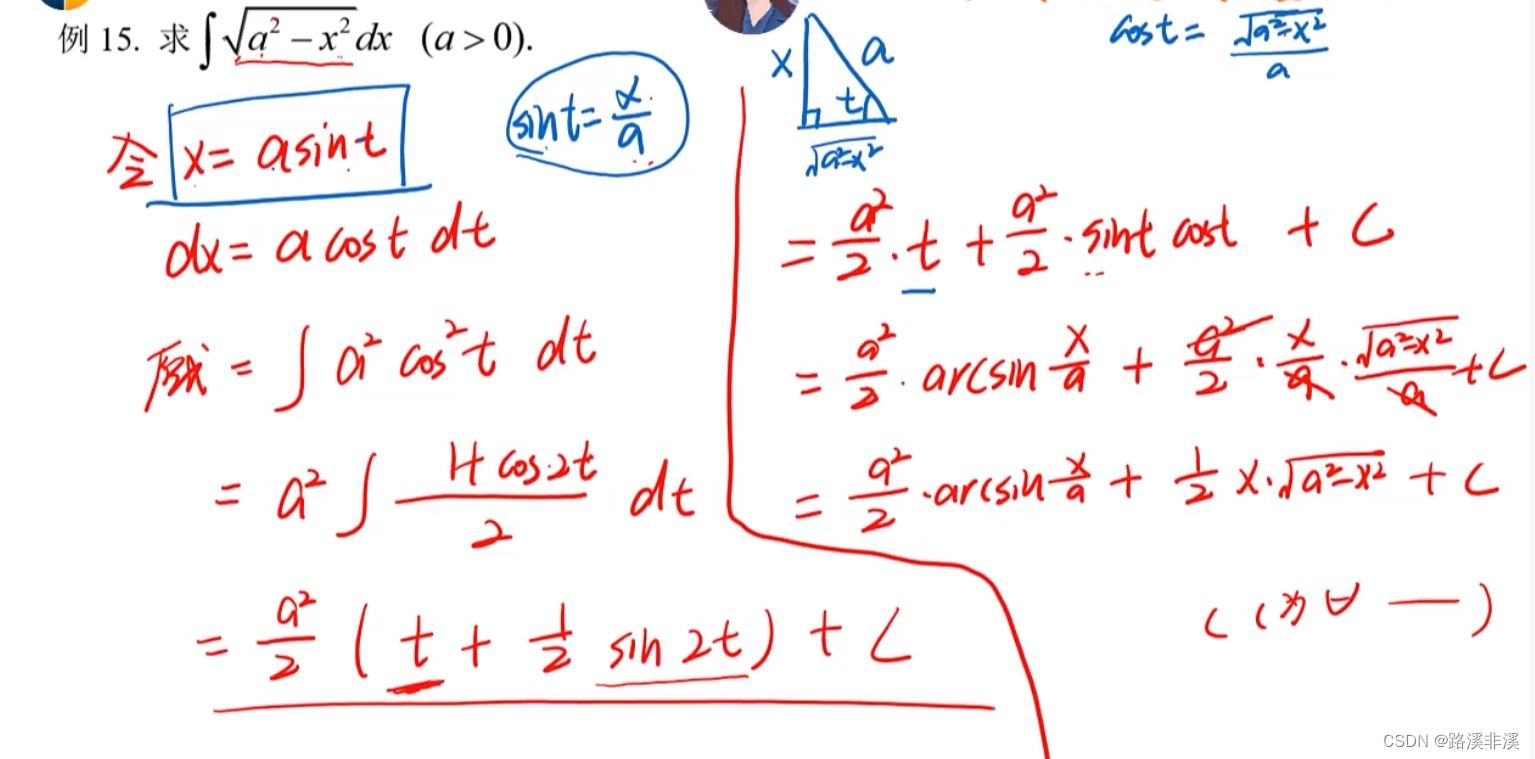
举个例子:
注意,左边求出来是关于t的结果,右边是将t还原成x。
分部积分法
口诀里的意思是
反三角函数、对数函数、幂函数、、指数函数、三角函数;
只有一类函数不要用这个方法,这个方法用于被积函数有以上两类函数的题目。
这个方法啥意思?
举个例子:
就是先将其中一类函数凑微分,然后按照式子展开,就能化简积分。
上面是关于不定积分的相关内容,一定要明确,不定积分就是一个导函数的原函数(带有任意常数项)
那么定积分呢?
定积分
引例
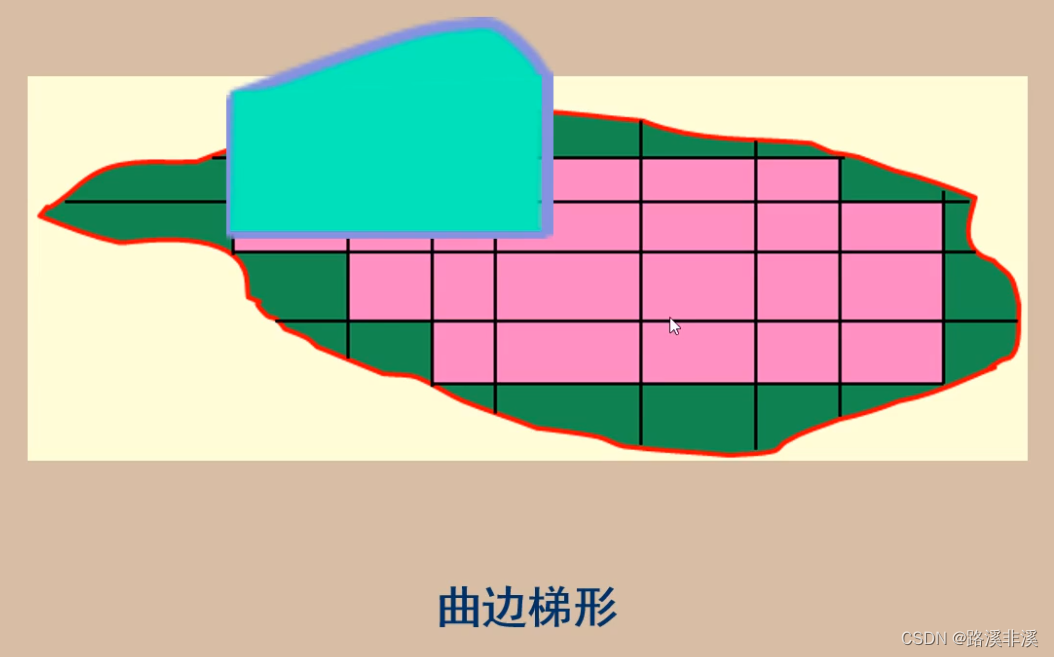
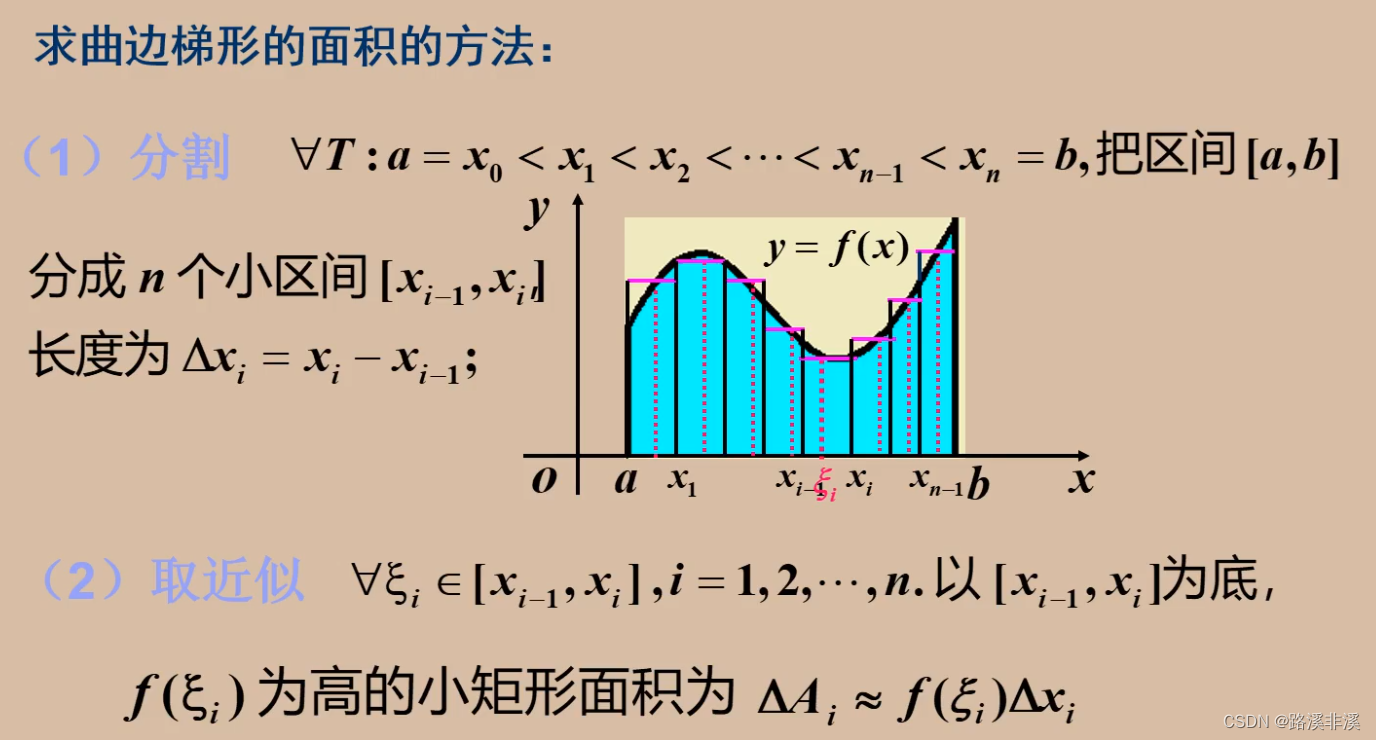
假如现在想要求一个湖泊的表面积,当获取模型之后,对其进行分割,其中含有完整矩形块的地方,面积很好求,可是有个问题,边沿的那些不规则的形状的面积,怎么计算呢?
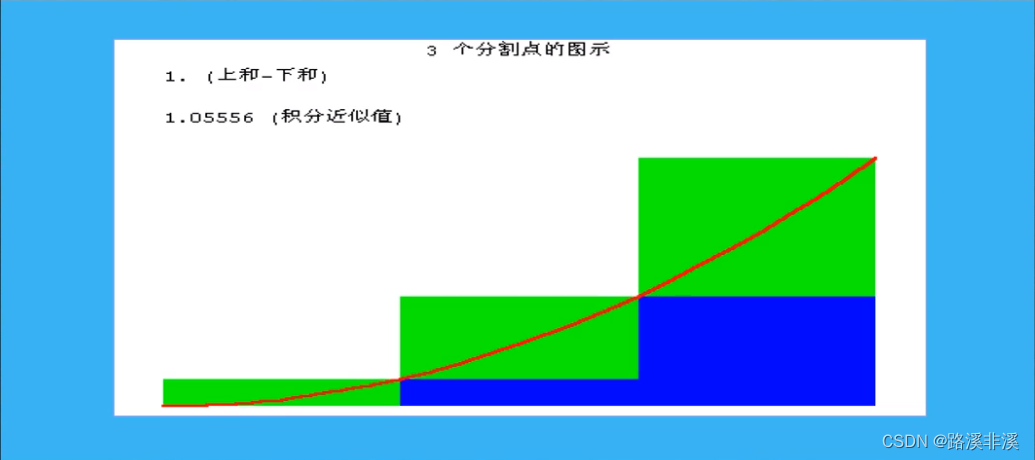
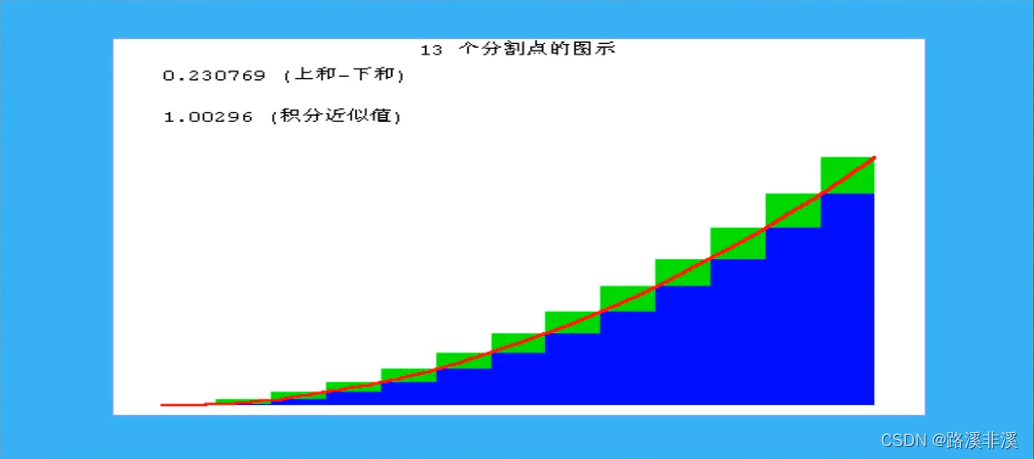
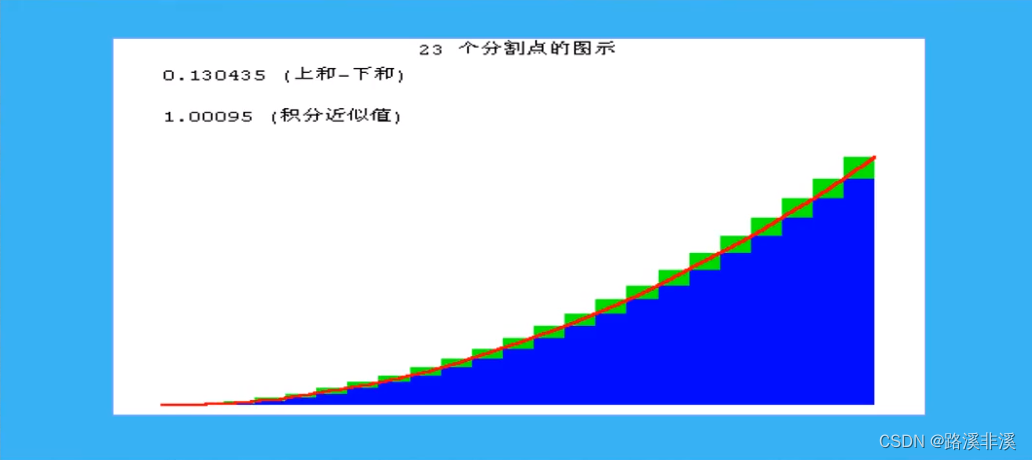
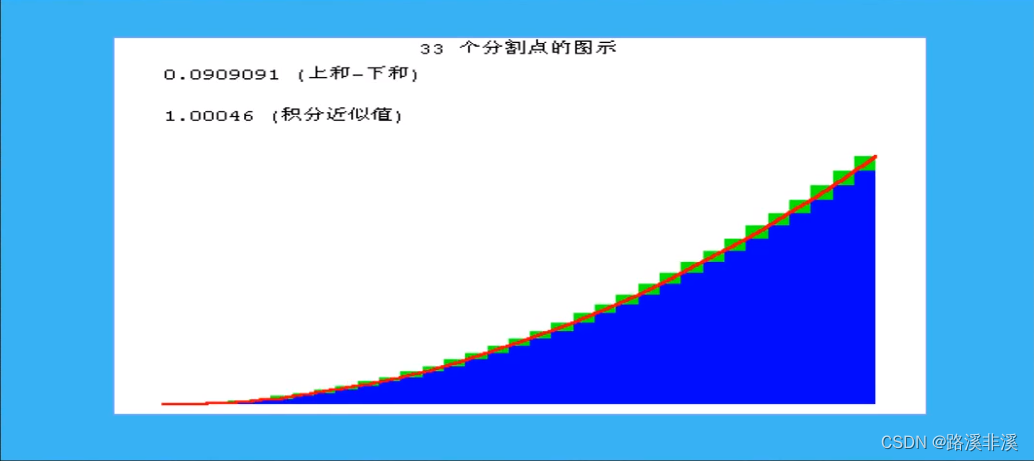
尝试求取曲边梯形的面积
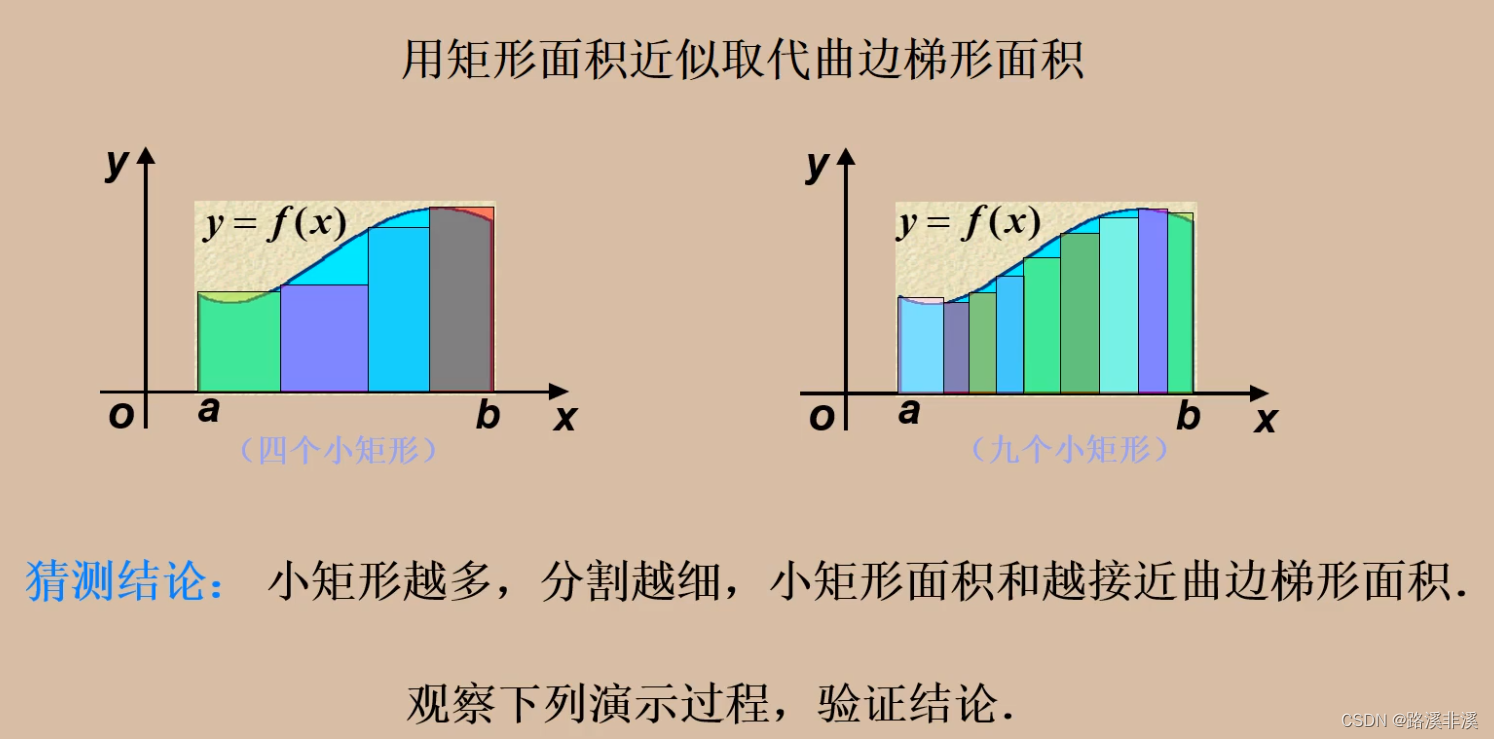
不断加大分割点
……
一直往后加,分割点越多,则矩形面积之和就越接近曲线所围成的面积。
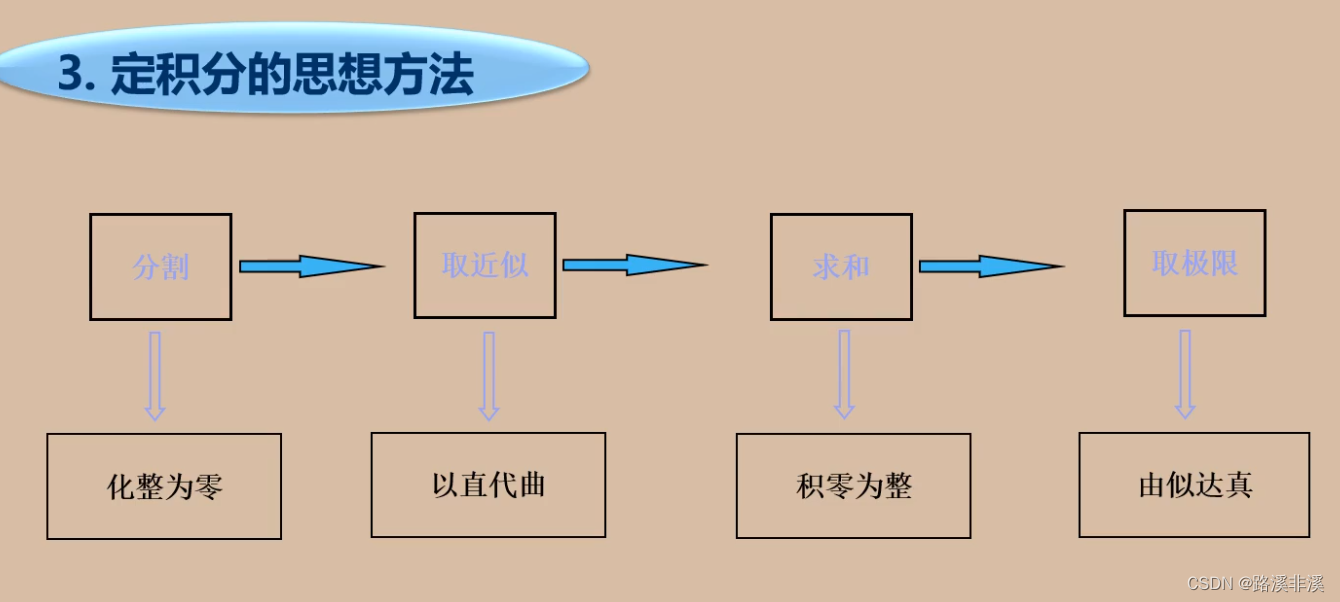
我们就尝试用这种思想来求曲边梯形的面积
上定义
从定义可知,定积分是个极限值,是个确定的常数,因此被叫做定积分。
不定积分得到的是个函数,是不确定的值;定积分得到的是个确定的值。
定积分又叫做黎曼积分。
黎曼积分(Riemann Integral),也就是所说的正常积分、定积分。在实分析中,由黎曼创立的黎曼积分首次对函数在给定区间上的积分给出了一个精确定义。黎曼积分在技术上的某些不足之处可由后来的黎曼-斯蒂尔杰斯积分和勒贝格积分得到修补。
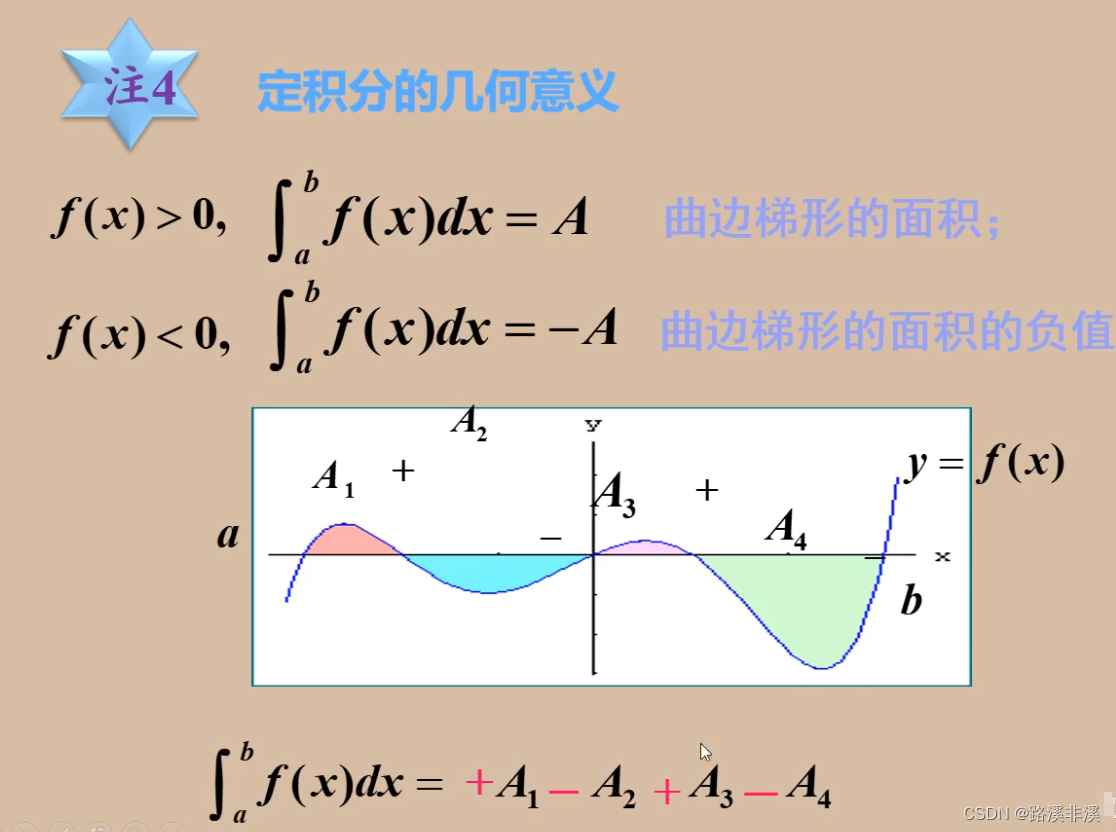
再看几何意义
其实就是曲线围成的面积的代数和。
上正下负,面积上多下少则整体为正,面积上少下多则整体为负。
注意:

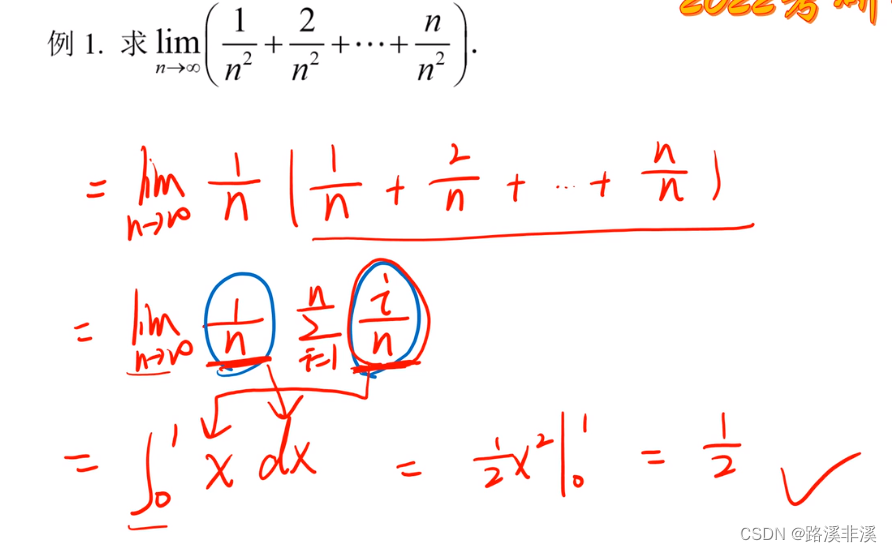
定积分求极限
ξi此时取的是每一个区间的结束点,只要在区间内,都是可以的。
举个例子:
可积的充分条件
定积分的性质
推论1
推论2:整体积分的绝对值小于等于绝对值的积分
这个从几何意义比较好理解,函数的绝对值是非负的,所以面积大于0,而整体可能是正负抵消后得出的面积代数和的绝对值。
估值定理
曲边梯形的面积必然在内矩形面积和外矩形面积之间。
定积分中值定理
曲边梯形的面积,肯定会等于其中一个矩形的面积大小,这个矩形面积介于最小的内矩形和最大的外矩形之间。
微积分基本公式
我们知道了定积分的定义和性质,那么问题来了,定积分怎么计算呢?
难道要用定义来求极限?
事实上,我们通常用不定积分来求定积分。
就是这么神奇,就是这么奇妙。
通常,我们用定积分用得比较多,因为定积分可以计算出一个结果,不定积分通常只是用来求解定积分的一个工具。
而定积分和不定积分,就是通过微积分基本公式联系起来的。
积分上限函数及其导数
因为定积分最终会将a和x带入t,所以变上限积分最后会变成一个关于x的函数。
性质
微积分基本公式,又叫微积分基本定理,又叫牛顿-莱布尼茨公式
根据这个定理,求定积分就是先求不定积分,然后将定积分上下限带入相减。
举个简单的例子
定积分的换元法和分部积分法和不定积分求法一样,不同的是变换和计算的时候要考虑上下限,暂时略。




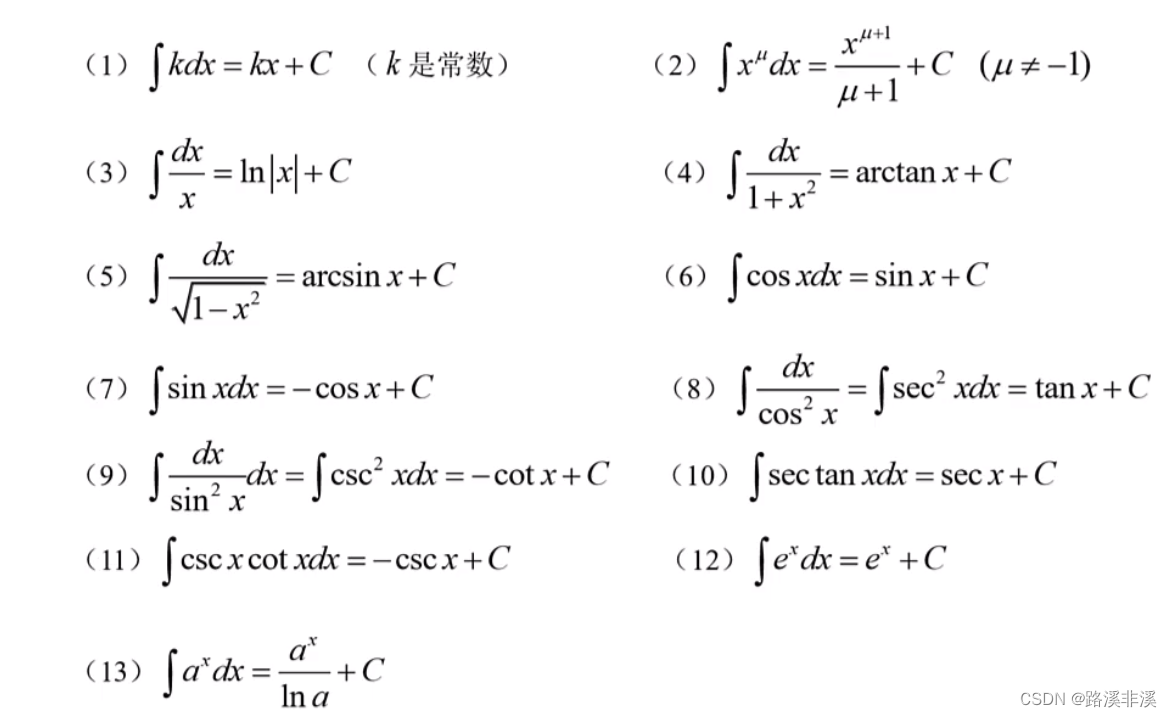


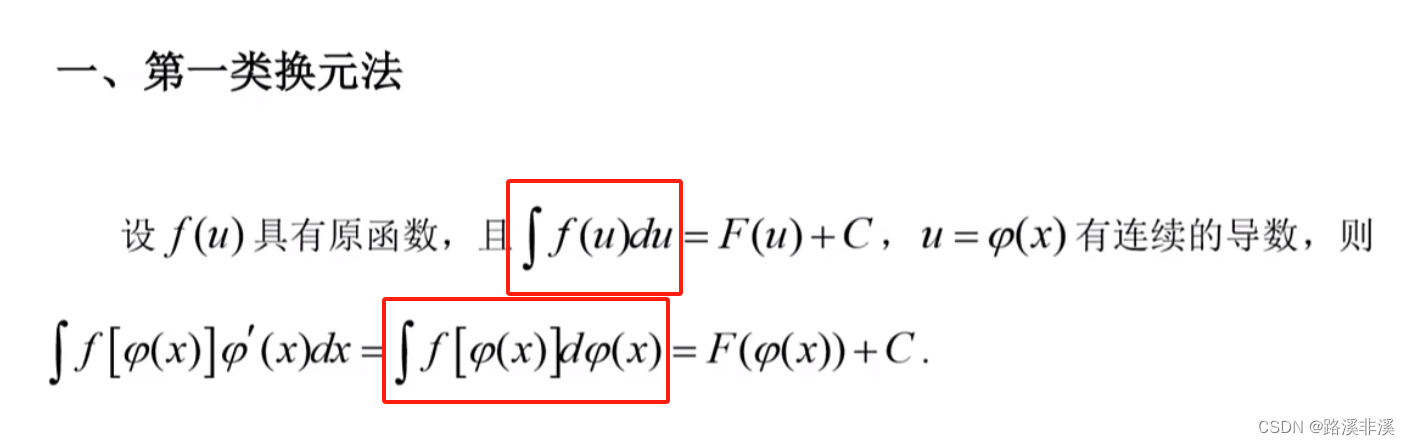



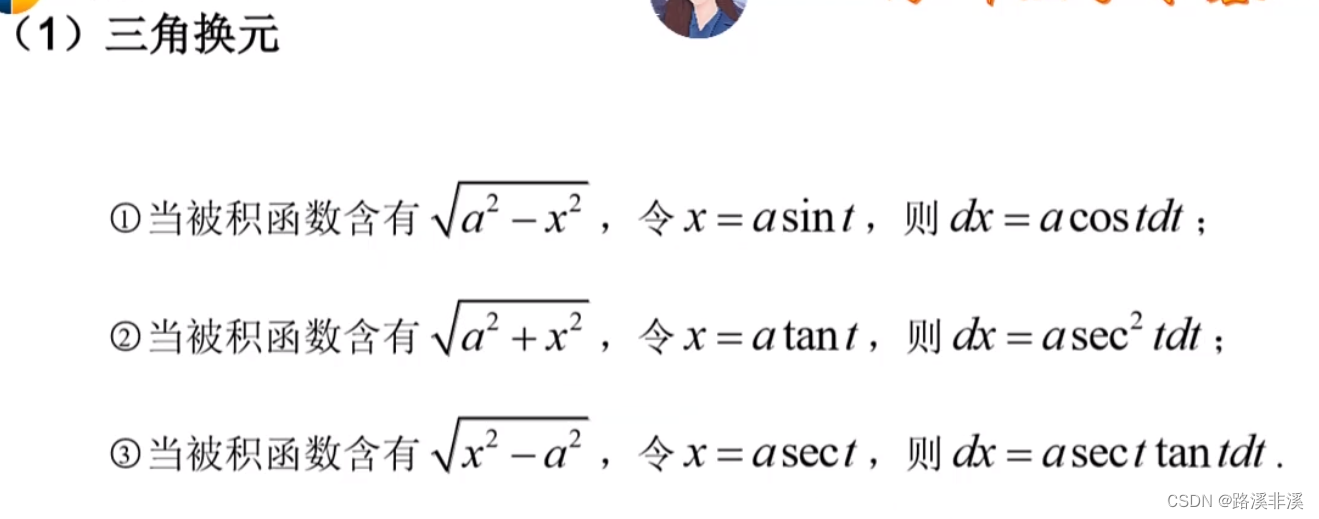



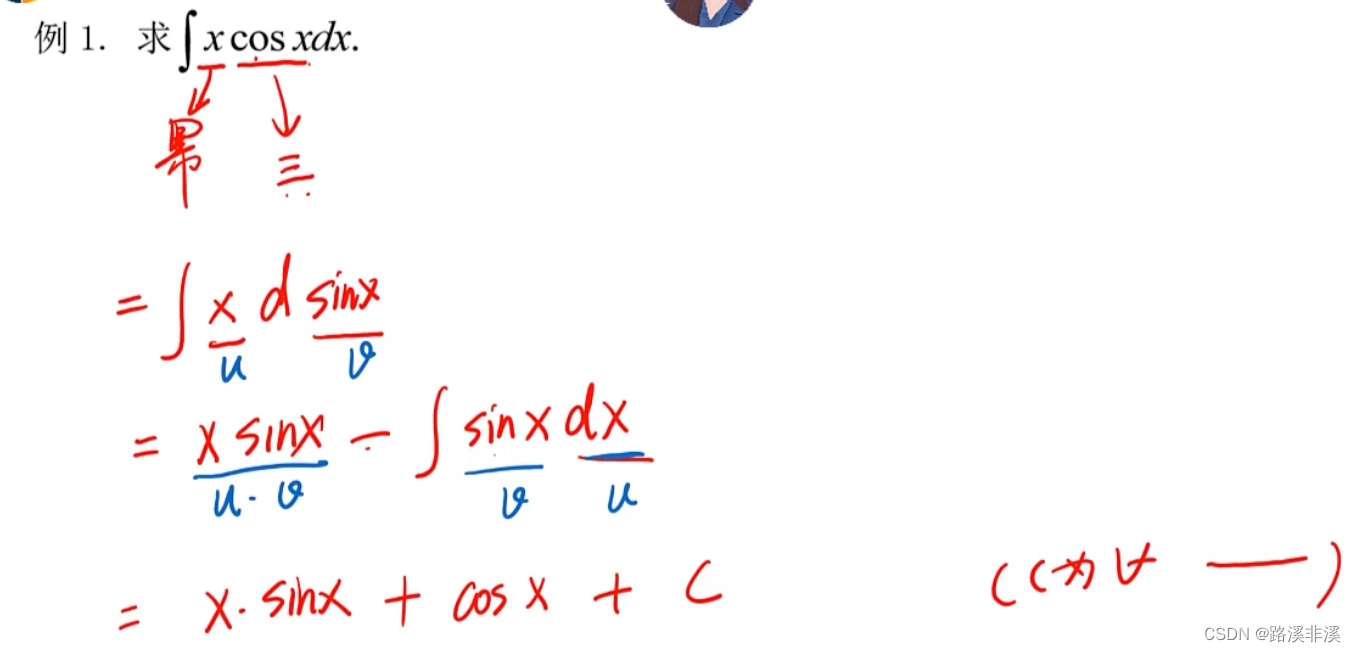







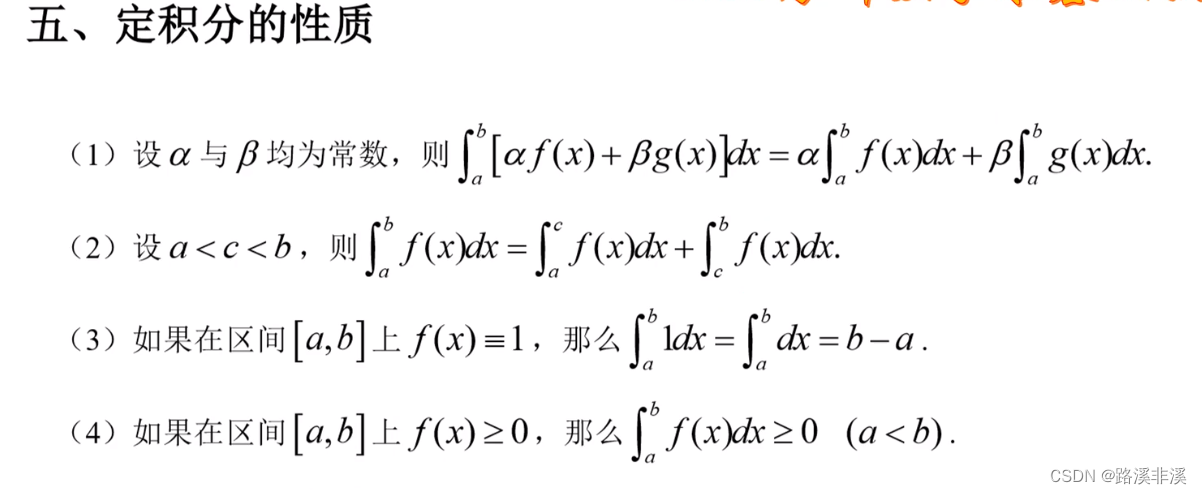
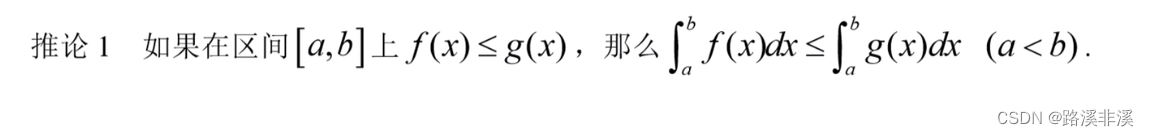
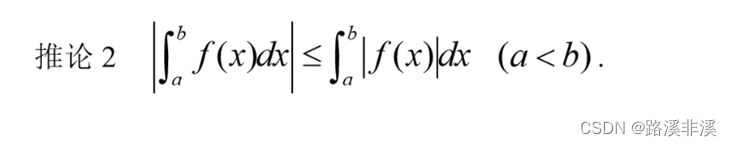

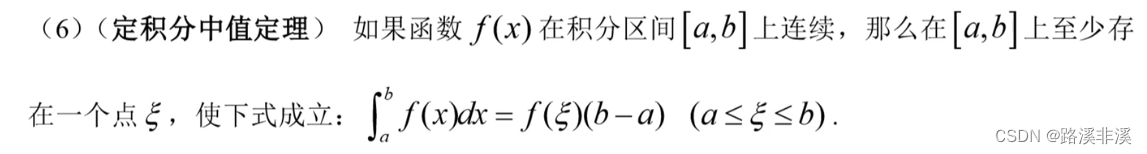






















)
